Théorie du module : Trigonométrie
Table des matières
- Angles
- Nombres trigonométriques
- Règle des sinus et Règle des cosinus
- Equations trigonométriques
- Exemples détaillés
Angles
(a) Définitions
points sur les côtés, on parlera de l'angle \(\widehat{AOB}\).
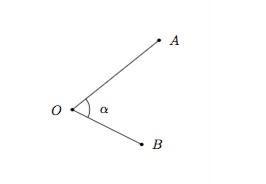
Un angle est souvent désigné par une lettre grecque minuscule telle \(\alpha\), \(\beta\), \(\gamma\) ou \(\theta\).
La mesure d'un angle s'exprime soit en degrés, soit en radians. Un angle de \(1\) degré correspond à \(\frac{1}{360}\) d'une rotation d'un tour complet dans le sens inverse des aiguilles d'une montre. La mesure d'un angle \(\alpha\), ou amplitude de l'angle, est la mesure de longueur \(s\) de l'arc \(AB\) (où \(A\) et \(B\) se trouvent sur le cercle unité centré en \(O\)).
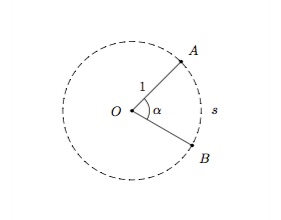
Lorsque \(s=1\), on dira que \(\alpha\) mesure \(1\) radian. Puisque la longueur du cercle unité est \(2\pi\), on obtient la correspondance suivante entre degrés et radians :
\begin{array}{c} 360^\circ=2\pi\mbox{ radians }\\ 1\mbox{ radian } = \displaystyle\frac{360^\circ}{2 \pi}= 57^\circ 17' 45''\dots \\ 1\mbox{ degré }= \displaystyle\frac{2 \pi }{360}\mbox{ radians } = 0,01745 \mbox{ radians} \end{array}
Un angle est aigu si son amplitude est inférieure à \(90^{\circ}\). Un angle droit est un angle dont l'amplitude est \(90^{\circ}\). Un angle est obtu si son amplitude est entre \(90^{\circ}\) et \(180^{\circ}\). Un angle plat est un angle dont l'amplitude est \(180^{\circ}\).
Deux angles ayant même amplitude sont dits congruents. Deux angles sont équivalents si la différence d'amplitude de ces angles est un multiple de \(360^\circ = 2\pi\) radians.
Des angles sont complémentaires si la somme de leurs amplitudes vaut \(90^{\circ}\). Des angles sont supplémentaires si la somme de leurs amplitudes vaut \(180^{\circ}\). Deux angles dont la différence des amplitudes vaut \(180^\circ\) sont dits anti-supplémentaires. Deux angles sont opposés si la somme de leurs amplitudes vaut \(0^{\circ}\).
Par exemple, si l'angle \(\alpha=30^{\circ}\) alors l'angle \(60^{\circ}\) est le complémentaire de \(\alpha\), l'angle \(150^{\circ}\) est le supplémentaire de \(\alpha\), l'angle \(210^{\circ}\) est l'anti-supplémentaire de \(\alpha\). L'angle \(-30^{\circ}\) est l'opposé de \(\alpha\) et l'angle \(750^{\circ}\) est équivalent à \(\alpha\).
(b) Positions relatives de deux angles
Deux angles sont adjacents s'ils ont le même sommet et un côté commun. Dans la figure ci-dessous, les angles \(\widehat{AOB}\) et \(\widehat{BOC}\) sont adjacents.
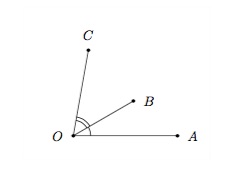
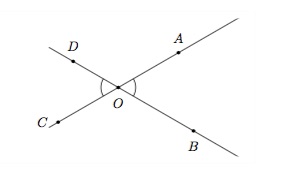
Deux angles sont opposés par le sommet s'ils ont même sommet et si leurs côtés sont les prolongements respectifs l'un de l'autre. Dans la figure ci-dessous, les angles \(\widehat{AOB}\) et \(\widehat{DOC}\) sont opposés par le sommet, ainsi que les angles \(\widehat{AOD}\) et \(\widehat{BOC}\).
Considérons deux droites parallèles \(d_1\) et \(d_2\) coupées par une droite \(d_3\). Soit \(A\) le point d'intersection de \(d_1\) et \(d_3\) et \(B\) le point d'intersection de \(d_2\) et \(d_3\).
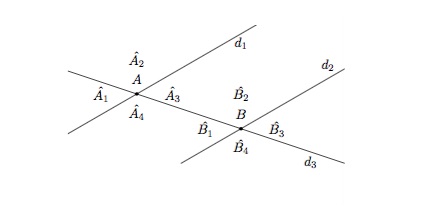
Deux angles sont correspondants s'ils n'ont pas le même sommet et se trouvent du même côté de la droite \(d_3\) et du même côté respectivement de la droite \(d_1\) et de la droite \(d_2\).
Par exemple, les angles \(\widehat{A_1}\) et \(\widehat{B_1}\) sont correspondants, les angles \(\widehat{A_2}\) et \(\widehat{B_2}\) sont correspondants, les angles \(\widehat{A_3}\) et \(\widehat{B_3}\) sont correspondants et les angles \(\widehat{A_4}\) et \(\widehat{B_4}\) sont correspondants.
Deux angles sont alternes internes s'ils n'ont pas le même sommet et se trouvent de part et d'autre de la droite \(d_3\) et entre les droites \(d_1\) et \(d_2\).
Par exemple, les angles \(\widehat{A_4}\) et \(\widehat{B_2}\) sont alternes internes. Et les angles \(\widehat{A_3}\) et \(\widehat{B_1}\) sont alternes internes.
Deux angles sont alternes externes s'ils n'ont pas le même sommet et se trouvent de part et d'autre de la droite \(d_3\) et à l'extérieur des droites \(d_1\) et \(d_2\).
Par exemple, les angles \(\widehat{A_1}\) et \(\widehat{B_3}\) sont alternes externes. Et les angles \(\widehat{A_2}\) et \(\widehat{B_4}\) sont alternes externes.
Propriétés
Deux angles correspondants ont même amplitude.
Deux angles alternes internes ont même amplitude.
Deux angles alternes externes ont même amplitude.
(c) Angles et cercles
On considère un cercle de centre \(O\) et \(A\), \(B\), \(C\) trois points de ce cercle.
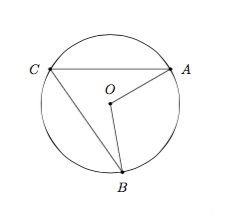
Un angle est inscrit dans un cercle si son sommet est un point du cercle et si ses deux côtés coupent le cercle en un deuxième point.
Par exemple, dans la figure ci-dessus, l'angle \(\widehat{ACB}\) est inscrit dans le cercle. Cet angle intercepte l'arc \(AB\).
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
Dans le cas particulier où l'angle inscrit dans un cercle intercepte un diamètre, on a le résultat suivant.
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
Un angle au centre d'un cercle a le centre de ce cercle comme sommet.
Par exemple, dans la figure ci-dessus, l'angle \(\widehat{AOB}\) est un angle au centre. Cet angle intercepte l'arc \(AB\).
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
Par exemple, dans la figure ci-dessus, l'amplitude de l'angle \(\widehat{AOB}\) vaut le double de l'amplitude de l'angle \(\widehat{ACB}\).
Nombres trigonométriques
(a) Définition des nombres trigonométriques
Le cercle trigonométrique est un cercle de rayon 1 centré à l'origine. On mesure l'angle \(\alpha\) à partir de l'axe horizontal; \(\alpha\) est positif dans le sens anti-horlogique et négatif dans le sens des aiguilles d'une montre. Les angles sont définis à \(2\pi\) près; ainsi l'angle \(\alpha\) est le même que les angles \(\alpha+2\pi\) , \(\alpha+4\pi\) , \(\alpha-2\pi\) , \(\ldots\) , \(\alpha+2k\pi\) , \(k\in \mathbb{Z}\) .
Les nombres trigonométriques sinus et cosinus, tangente et cotangente sont définis pour un angle \(\alpha\) donné comme le montre la figure suivante.
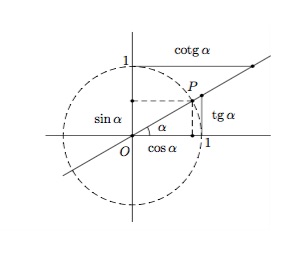
Définitions - Soit \(P\) un point du cercle trigonométrique faisant un angle \(\alpha\) avec l'axe horizontal. L'abscisse de \(P\) est appelée cosinus \(\alpha\) et l'ordonnée de \(P\) est appelée sinus \(\alpha\).
L'ordonnée du point d'abscisse \(1\) de la droite \(OP\) est appelée tangente \(\alpha\) et l'abscisse du point d'ordonnée \(1\) de la droite \(OP\) est appelée cotangente \(\alpha\).
Les coordonnées du point \(P\) sont donc \((\cos\alpha,\sin\alpha)\) et on a toujours
\begin{array}[t]{c} -1\leq\cos\alpha\leq 1\mbox{ et }-1\leq\sin\alpha\leq 1 \end{array}
On déduit du Théorème de Pythagore la formule fondamentale suivante :
\(\sin^2\alpha+\cos^2\alpha=1\)
Considérons les triangles rectangles \(OAB\) et \(OA'B'\).
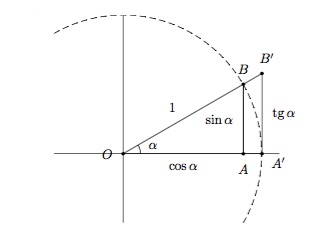
Ces deux triangles sont semblables et par les propriétés des triangles semblables, on a donc
\(tg\,\alpha=\frac{\sin\alpha}{\cos\alpha}.\)
Remarquons que le nombre \(tg\,\alpha\) n'est défini que pour \(\alpha\neq\frac{\pi}{2}+k\pi\), \(k\in \mathbb{Z}\). De même, on a
\(cotg\,\alpha=\frac{\cos\alpha}{\sin\alpha}=\frac{1}{tg\, \alpha},\)
où \(\alpha\neq k\pi\), \(k\in \mathbb{Z}\).
Toujours en utilisant les propriétés des triangles semblables, on a
\(\displaystyle\frac{|AB|}{|OB|}=\frac{|AB|}{1}=\sin\alpha,\)
d'où
\(\begin{array}[t]{c} \sin\alpha=\displaystyle\frac{\mbox{côté opposé à }\alpha}{\mbox{hypoténuse}}. \end{array}\)
De même, on a
\(\displaystyle\frac{|OA|}{|OB|}=\frac{|OA|}{1}=\cos\alpha, \)
d'où
\(\begin{array}[t]{c} \cos\alpha=\displaystyle\frac{\mbox{côté adjacent à }\alpha}{\mbox{hypoténuse}}. \end{array}\)
On en déduit que
\(\begin{array}[t]{c} tg\,\alpha=\displaystyle\frac{\sin\alpha}{\cos\alpha}=\frac{\mbox{côté opposé à }\alpha}{\mbox{côté adjacent à }\alpha}. \end{array}\)
Par exemple, si \(\alpha\) est un angle aigu et \(\cos \alpha = \frac{3}{4}\), on peut calculer les valeurs des nombres trigonométriques de \(\alpha\). Commençons par dessiner un triangle rectangle ayant un angle aigu \(\alpha\) avec "côté adjacent" =3 et "hypoténuse" =4.
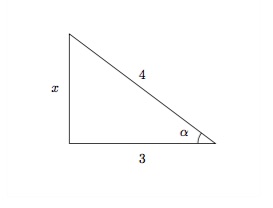
Soit \(x\) le côté opposé à \(\alpha\). Par le Théorème de Pythagore, on a
\(3^2 + x^2 = 4^2,\)
d'où \(x = \sqrt{16-9} = \sqrt{7}\). On en déduit
\(\begin{array}{ll} \sin \alpha = \frac{\mbox{opposé}}{\mbox{hypoténuse}}=\displaystyle\frac{\sqrt{7}}{4},&\hspace{3cm} tg\, \alpha = \frac{\mbox{opposé}}{\mbox{adjacent}}=\displaystyle\frac{\sqrt{7}}{3},\\[2mm] \cos \alpha = \frac{\mbox{adjacent}}{\mbox{hypoténuse}}=\displaystyle\frac{3}{4},&\hspace{3cm} cotg\, \alpha = \frac{\mbox{adjacent}}{\mbox{opposé}}=\displaystyle\frac{3}{\sqrt{7}}=\frac{3\sqrt{7}}{7}. \end{array}\)
Voici quelques valeurs remarquables des nombres trigonométriques.
\(\begin{array}{c|cccccc} \alpha&\hspace{4mm}0&\hspace{4mm}\displaystyle\frac{\pi}{6}&\hspace{4mm}\displaystyle\frac{\pi}{4}&\hspace{4mm}\displaystyle\frac{\pi}{3} &\hspace{4mm}\displaystyle\frac{\pi}{2}&\hspace{4mm}\pi\\[2mm] \hline \sin\alpha\hspace{2mm}&\hspace{4mm}0&\hspace{4mm}\displaystyle\frac{1}{2}&\hspace{4mm}\displaystyle\frac{\sqrt{2}}{2} &\hspace{4mm}\displaystyle\frac{\sqrt{3}}{2}&\hspace{4mm}1&\hspace{4mm}0\\[2mm] \cos\alpha\hspace{2mm}&\hspace{4mm}1&\hspace{4mm}\displaystyle\frac{\sqrt{3}}{2}&\hspace{4mm}\displaystyle\frac{\sqrt{2}}{2} &\hspace{4mm}\displaystyle\frac{1}{2}&\hspace{4mm}0&\hspace{4mm}-1\\[2mm] tg\,\alpha\hspace{2mm}&\hspace{4mm}0&\hspace{4mm}\displaystyle\frac{\sqrt{3}}{3}&\hspace{4mm}1&\hspace{4mm}\sqrt{3} &\hspace{4mm}/&\hspace{4mm}0 \end{array}\)
(b) Propriétés des nombres trigonométriques
Le calcul d'un nombre trigonométrique d'un angle donné peut se ramener au calcul d'un nombre trigonométrique d'un angle du premier quadrant. A partir des valeurs données dans la table ci-dessus, on peut déduire les valeurs d'autres nombres trigonométriques grâce aux formules ci-dessous.
Pour des angles opposés \(\alpha\) et \(-\alpha\)
Dans un cercle trigonométrique, deux angles opposés sont représentés par deux points du cercle symétriques par rapport à l'axe \(OX\).
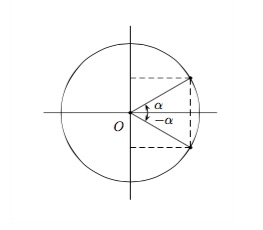
\(\begin{array}{ll} \sin ( -\alpha) = - \sin \alpha\hspace{2cm}&tg\,( -\alpha) = - tg\,\alpha\\ \cos ( -\alpha) = \cos \alpha&cotg\,( -\alpha) = - cotg\,\alpha \end{array}\)
Pour des angles complémentaires \(\alpha\) et \({\pi \over 2} -\alpha\)
Dans un cercle trigonométrique, deux angles complémentaires sont représentés par deux points du cercle symétriques par rapport à la droite \(y=x\).
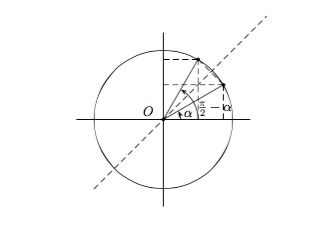
\(\begin{array}{ll} \sin ({\pi \over 2} -\alpha) = \cos \alpha\hspace{2cm}&tg\,({\pi \over 2} -\alpha) = cotg\, \alpha\\ \cos ({\pi \over 2} -\alpha) = \sin \alpha&cotg\,({\pi \over 2} -\alpha) = tg\,\alpha \end{array}\)
Pour des angles supplémentaires \(\alpha\) et \(\pi -\alpha\)
Dans un cercle trigonométrique, deux angles supplémentaires sont représentés par deux points du cercle symétriques par rapport à l'axe \(OY\).
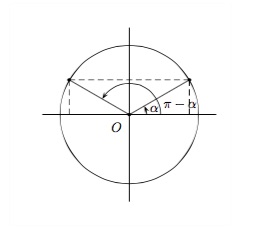
\(\begin{array}{ll} \displaystyle \sin (\pi -\alpha) = \sin \alpha\hspace{2cm}&tg\,(\pi -\alpha) = - tg\, \alpha\\ \displaystyle \cos (\pi -\alpha) = - \cos \alpha&cotg\,(\pi -\alpha) = - cotg\, \alpha \end{array}\)
Pour des angles anti-supplémentaires \(\alpha\) et \(\pi+\alpha\)
Dans un cercle trigonométrique, deux angles anti-supplémentaires sont représentés par deux points du cercle symétriques par rapport à l'origine \(O\).
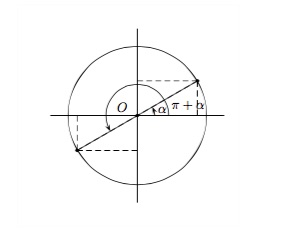
\(\begin{array}{ll} \displaystyle \sin (\pi +\alpha) = - \sin \alpha\hspace{2cm}&tg\,(\pi +\alpha) = tg\,\alpha\\ \displaystyle \cos (\pi +\alpha) = - \cos \alpha&cotg\,(\pi +\alpha) = cotg\,\alpha \end{array}\)
(c) Formules trigonométriques
Les formules suivantes relient les différents nombres trigonométriques.
Formule fondamentale
\(\sin^2 \alpha + \cos ^2 \alpha = 1\)
Formules de duplication
\(\sin (2\alpha) = 2 \sin \alpha \cos \alpha\)
\(\cos (2\alpha) = \cos ^2 \alpha - \sin ^2 \alpha = 1 - 2 \sin ^2 \alpha = 2 \cos ^2 \alpha - 1\)
\(\displaystyle tg\,{(2\alpha)} = \frac{2\, tg\,{\alpha}} {1- tg^2{\alpha}}\)
Formules d'addition
\(\begin{array}{ll} \sin (\alpha + \beta) = \sin \alpha \cos\beta + \sin \beta \cos \alpha &\hspace{1.5cm}\sin (\alpha -\beta) = \sin \alpha \cos\beta - \sin \beta \cos\alpha\\ \cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \beta \sin\alpha &\hspace{1.5cm}\cos (\alpha - \beta) = \cos \alpha \cos\beta + \sin \beta \sin \alpha\\ \displaystyle tg\, (\alpha + \beta) = \frac{tg\, \alpha+ tg\, \beta}{1- tg\,\alpha \cdot tg\, \beta} &\hspace{1.5cm}\displaystyle tg\, (\alpha - \beta) = {tg\,\alpha - tg\, \beta \over 1+ tg\, \alpha \cdot tg\, \beta} \end{array}\)
Formules de Carnot
\(\begin{array}{ll} \displaystyle \sin ^ 2 \alpha = {1 - \cos (2\alpha) \over 2}&\hspace{1.5cm} \displaystyle 1+tg^2 \alpha = {1\over \cos^2 \alpha}\\ \displaystyle \cos ^ 2 \alpha = {1 + \cos (2\alpha) \over 2}&\hspace{1.5cm} \displaystyle 1+cotg^2 \alpha = {1\over \sin^2 \alpha} \end{array}\)
Formules de Simpson
\(\begin{array}{l} \sin \alpha + \sin \beta = 2 \sin {(\frac{\alpha +\beta} {2})} \cos {(\frac{\alpha -\beta}{2})}\\[1mm] \sin \alpha - \sin \beta = 2 \sin {(\frac{\alpha -\beta}{2})} \cos {(\frac{\alpha +\beta} {2})}\\[1mm] \cos \alpha + \cos \beta = 2 \cos {(\frac{\alpha +\beta} {2})} \cos {(\frac{\alpha -\beta}{2})}\\[1mm] \cos \alpha - \cos \beta = -2 \sin {(\frac{\alpha -\beta}{2})} \sin {(\frac{\alpha +\beta}{2})} \end{array}\)
Règle des sinus et Règle des cosinus
Le résultat suivant permet de trouver la longueur d'un côté d'un triangle quelconque si on connaît la longueur d'un autre côté et les deux angles opposés. Il permet également de déterminer un angle si on en connaît un autre et la longueur de leurs côtés opposés.
Règle des sinus - Dans tout triangle, les longueurs des côtés sont proportionnelles aux sinus des angles opposés, c'est-à-dire si \(a\), \(b\) et \(c\) sont les longueurs des côtés d'un triangle et \(\alpha\), \(\beta\) et \(\gamma\) sont les angles opposés respectivement à ces côtés, on a
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}.\)
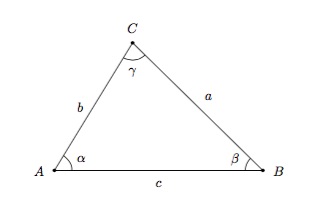
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
Voici un exemple d'application de ce résultat. Lorsque l'angle d'élévation du soleil est de \(64^\circ\), un poteau téléphonique qui penche d'un angle de \(9^\circ\) par rapport à une ligne formée par le pied du poteau et le soleil projette une ombre de 6,3 mètres sur le sol. On cherche la hauteur du poteau.
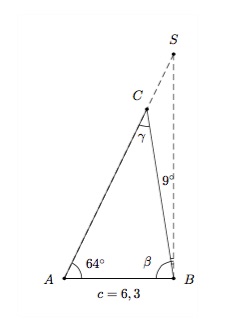
Le triangle \(ABC\) (avec \(\alpha= 64^\circ\), \(\beta =90^\circ - 9^\circ = 81^\circ\) et \(\gamma = 180^\circ- 64^\circ-81^\circ = 35^\circ\)) représente les faits. Pour calculer la hauteur du poteau, c'est-à-dire le côté \(a=BC\) du triangle \(ABC\), on utilise la Règle des sinus :
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \gamma}{c},\)
c'est-à-dire
\(\dfrac{\sin 64^\circ}{a}=\dfrac{\sin 35^\circ}{6,3},\)
d'où \(a=6,3\cdot \frac{\sin 64^\circ}{\sin 35^\circ}=9,87\) mètres.
Le résultat suivant est une généralisation du Théorème de Pythagore. Il permet de trouver la longueur d'un des côtés à partir de celle des deux autres et de l'angle compris entre ces deux autres côtés. Il porte le nom de règle des cosinus ou encore règle de Pythagore généralisée.
Règle des cosinus - Dans tout triangle, le carré de la longueur d'un côté est égal à la somme des carrés des longueurs des deux autres côtés diminuée du double produit des longueurs de ces deux côtés par le cosinus de l'angle compris entre ces côtés, c'est-à-dire si \(a\), \(b\) et \(c\) sont les longueurs des côtés d'un triangle et \(\alpha\), \(\beta\) et \(\gamma\) sont les angles opposés respectivement à ces côtés, on a
\(\begin{array}{l} a^2=b^2+c^2-2bc\cos{\alpha} \\ b^2=a^2+c^2-2ac\cos{\beta} \\ c^2=a^2+b^2-2ab\cos{\gamma} \end{array}\)
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
Voici un exemple d'application de ce résultat. Sur le flanc d'une montagne se trouve une tour. Un observateur se trouvant à 320 mètres de la tour la voit sous un angle de \(6^{\circ}\). Il monte alors dans la direction de la tour et, après avoir parcouru 220 mètres, il la voit sous un angle de \(13^{\circ}\). On cherche la hauteur de cette tour. Schématisons la situation.
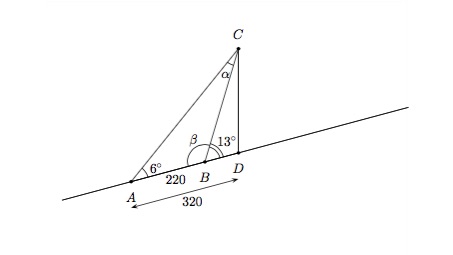
On déduit des données que l'angle \(\beta=180^{\circ}-13^{\circ}=167^{\circ}\), donc l'angle \(\alpha=180^{\circ}-167^{\circ}-6^{\circ}=7^{\circ}\).
On déduit la longueur du côté \(AC\) de la Règle des sinus :
\(\dfrac{220}{\sin{7^{\circ}}}=\dfrac{\vert AC\vert}{\sin{167^{\circ}}}\)
et donc \(\vert AC\vert=220\cdot \dfrac{\sin{167^{\circ}}}{\sin{7^{\circ}}}=406,1\) mètres.
Finalement, par la Règle des cosinus, on obtient
\(\begin{array}{rcl} h^2=\vert CD\vert^2 &= &\vert AD\vert^2+\vert AC\vert^2-2\vert AD\vert\, \vert AC\vert\, \cos{6^{\circ}} \\ & = &320^2+\left( 220\cdot \dfrac{\sin{167^{\circ}}}{\sin{7^{\circ}}}\right)^2 -2\cdot 320\cdot \left( 220\cdot \dfrac{\sin{167^{\circ}}}{\sin{7^{\circ}}}\right) \cdot\cos{6^{\circ}} \\ & = &8836,99 \end{array}\)
et donc \(h=\sqrt{h^2}\approx 94\) mètres.
Equations trigonométriques
(a) Equations fondamentales
Cherchons tous les angles \(x\) tels que \(\sin x = m\) où \(m \in [-1,1]\).
Soit \(\alpha\) une solution. Par les propriétés des nombres trigonométriques, on sait que deux angles supplémentaires ont même sinus. Donc, si \(\alpha\) est une solution, alors l'ensemble des solutions est
\(S= \{ x~: x= \alpha + 2k\pi \ \ {\rm ou }\ \ x = (\pi - \alpha)+2k\pi; k\in \mathbb{Z} \}.\)
Cherchons tous les angles \(x\) tels que \(\cos x = m\) où \(m \in [-1,1]\).
Soit \(\alpha\) une solution. Par les propriétés des nombres trigonométriques, on sait que deux angles opposés ont même cosinus. Donc, si \(\alpha\) est une solution, alors l'ensemble des solutions est
\(S= \{ x~: x= \alpha + 2k\pi \ \ {\rm ou }\ \ x = - \alpha +2k\pi; k\in \mathbb{Z} \}.\)
Cherchons tous les angles \(x\) tels que \(tg\,{x}= m\) où \(m \in \mathbb{R}\).
Soit \(\alpha\) une solution. Par les propriétés des nombres trigonométriques, on sait que deux angles anti-supplémentaires ont même tangente. Donc, si \(\alpha\) est une solution, alors l'ensemble des solutions est
\(S= \{ x~: x= \alpha + 2k\pi \ \ {\rm ou }\ \ x = (\pi + \alpha) +2k\pi; k\in \mathbb{Z} \}\)
ou encore
\(S=\{ x~: x= \alpha + k\pi; k\in \mathbb{Z} \}.\)
Par exemple, on cherche tous les angles \(x\) tels que \(\sin x = {1\over 2}\). Une solution est \(x = {\pi \over 6}\).
L'ensemble des solutions est
\(S= \left\{ \dfrac{\pi}{6} + 2k\pi, \, \dfrac{5\pi}{6} +2k\pi;\, k\in \mathbb{Z} \right\}.\)
Cherchons tous les angles \(x\) tels que \(tg\,{x} = -1\). Une solution est \(x = -{\pi \over 4}\).
L'ensemble des solutions est
\(S= \left\{ -\dfrac{\pi}{4} + k\pi;\, k \in \mathbb{Z} \right\}.\)
(b) Equations élémentaires
Cherchons tous les angles \(x\) tels que \(\sin x = \sin \alpha\).
Par les propriétés des nombres trigonométriques, on sait que deux angles ont le même sinus s'ils sont égaux (à \(2k\pi\)-près) ou s'ils sont supplémentaires (à \(2k\pi\)-près). L'ensemble des solutions est donc
\(S= \{ x~: x= \alpha + 2k\pi \ \ {\rm ou }\ \ x = (\pi - \alpha) +2k\pi; k\in \mathbb{Z} \}.\)
Cherchons tous les angles \(x\) tels que \(\cos x = \cos \alpha\).
Par les propriétés des nombres trigonométriques, on sait que deux angles ont le même cosinus s'ils sont égaux (à \(2k\pi\)-près) ou s'ils sont opposés (à \(2k\pi\)-près). L'ensemble des solutions est donc
\(S= \{ x~: x= \alpha + 2k\pi \ \ {\rm ou }\ \ x = - \alpha +2k\pi; k\in \mathbb{Z} \}.\)
Cherchons tous les angles \(x\) tels que \(tg\, x = tg\, \alpha\).
Par les propriétés des nombres trigonométriques, on sait que deux angles ont la même tangente s'ils sont égaux (à \(2k\pi\)-près) ou s'ils sont anti-supplémentaires (à \(2k\pi\)-près). L'ensemble des solutions est donc
\(S= \{ x~: x= \alpha + 2k\pi \ \ {\rm ou }\ \ x = (\pi + \alpha) +2k\pi; k\in \mathbb{Z} \}\)
c'est-à-dire
\(S= \{ x~: x= \alpha + k\pi; k\in \mathbb{Z} \}.\)
Par exemple, résolvons l'équation \(\sin{(3x+20^{\circ})} = \sin{(x+50^{\circ})}\). Il faut que
\(\begin{array}{lcl} 3x+20^{\circ}=x+50^{\circ}+k\cdot 360^{\circ}&\mbox{ ou }&3x+20^{\circ}=180^{\circ}-(x+50^{\circ})+k\cdot 360^{\circ}\\ 2x=30^{\circ}+k\cdot 360^{\circ}&\mbox{ ou }&4x=110^{\circ}+k\cdot 360^{\circ}\\ x=15^{\circ}+k\cdot 180^{\circ}&\mbox{ ou }&x=27^{\circ}30'+k\cdot 90^{\circ}\\ \end{array}\)
L'ensemble des solutions est donc
\(S= \{15^{\circ}+k\cdot 180^{\circ},\, 27^{\circ}30'+k\cdot 90^{\circ};\, k\in \mathbb{Z} \}.\)
Résolvons l'équation \(\cos{(x+\frac{\pi}{2})} = \cos{(3x)}\). Il faut que
\(\begin{array}{lcl} x+\dfrac{\pi}{2}=3x+2k\pi&\mbox{ ou }&x+\dfrac{\pi}{2}=-3x+2k\pi\\ -2x=-\dfrac{\pi}{2}+2k\pi&\mbox{ ou }&4x=-\dfrac{\pi}{2}+2k\pi\\ x=\dfrac{\pi}{4}+k\pi&\mbox{ ou }&x=-\dfrac{\pi}{8}+k\dfrac{\pi}{2}\\ \end{array}\)
L'ensemble des solutions est donc
\(S= \left\{\dfrac{\pi}{4}+k\pi,\, -\dfrac{\pi}{8}+k\dfrac{\pi}{2};\, k\in \mathbb{Z} \right\}.\)
(c) Equations générales
Si l'équation est plus générale, on utilise les propriétés des nombres trigonométriques pour se ramener à une équation fondamentale ou élémentaire.
Par exemple, cherchons tous les angles \(x\) tels que \(\sin{(x+\frac{\pi}{3})} = \cos{(2x)}\). On peut récrire cette équation
\(\cos{(\frac{\pi}{2}-(x+\frac{\pi}{3}))} = \cos{(2x)}\)
ou encore
\(\cos{(\frac{\pi}{6}-x)} = \cos{(2x)}.\)
Il faut donc que
\(\begin{array}{lcl} \dfrac{\pi}{6}-x=2x+2k\pi&\mbox{ ou }&\dfrac{\pi}{6}-x=-2x+2k\pi\\ -3x=-\dfrac{\pi}{6}+2k\pi&\mbox{ ou }&x=-\dfrac{\pi}{6}+2k\pi\\ x=\dfrac{\pi}{18}+2k\dfrac{\pi}{3}&\mbox{ ou }&x=-\dfrac{\pi}{6}+2k\pi\\ \end{array}\)
L'ensemble des solutions est donc
\(S= \left\{\dfrac{\pi}{18}+k\dfrac{2\pi}{3},\, -\dfrac{\pi}{6}+2k\pi;\, k\in \mathbb{Z} \right\}.\)
Dans le cas d'une équation du second degré, on commencera par faire un changement de variable pour se ramener à une équation du second degré classique que l'on résoud. On est alors ramené à une équation fondamentale ou élémentaire.
Pour plus de détails concernant la résolution des équations du second degré, cliquez ici.
Par exemple, cherchons tous les angles \(x\) tels que \(2\sin^2{x}-\sin{x}=1\).
Posons \(t=\sin{x}\). L'équation peut se récrire \(2t^2-t-1=0\). Les racines de cette équation sont \(t=1\) et \(t=-\frac{1}{2}\).
- Si \(t=\sin{x}=1\) alors \(x=\frac{\pi}{2}+2k\pi,\, k\in\mathbb{Z}\).
- Si \(t=\sin{x}=-\frac{1}{2}\) alors \(x=\frac{7\pi}{6}+2k\pi\) ou \(x=\frac{1\mbox{} 1\pi}{6}+2k\pi\), \(k\in\mathbb{Z}\).
Les solutions de cette équation sont donc
\(S=\left\{\dfrac{\pi}{2}+2k\pi,\, \dfrac{7\pi}{6}+2k\pi,\, \dfrac{11\pi}{6}+2k\pi;\, k\in\mathbb{Z}\right\}.\)
Exemples détaillés
-
Convertir les angles \(150^{\circ}\), \(-135^{\circ}\) et \(390^{\circ}\) en radians.
Solution détaillée : La formule permettant de passer de degrés en radians est
\(1\mbox{ degré }= \dfrac{2 \pi }{360}\mbox{ radians }= \dfrac{\pi }{180}\mbox{ radians}.\)
On obtient donc
\(150^{\circ}=150\cdot\dfrac{\pi }{180}\mbox{ radians }=\dfrac{5\pi}{6}\mbox{ radians}\);
\(-135^{\circ}=-135\cdot\dfrac{\pi }{180}\mbox{ radians }=-\dfrac{3\pi}{4}\mbox{ radians }=\dfrac{5\pi}{4}\mbox{ radians}\);
\(390^{\circ}=30^{\circ}=30\cdot\dfrac{\pi }{180}\mbox{ radians }=\dfrac{\pi}{6}\mbox{ radians}\).
-
Convertir en degrés les angles \(\dfrac{\pi}{12}\), \(\dfrac{2\pi}{3}\) et \(-\dfrac{\pi}{4}\).
Solution détaillée : La formule permettant de passer de radians en degrés est
\(1\mbox{ radian } = \dfrac{360^\circ}{2 \pi}= \dfrac{180^\circ}{\pi}.\)
On obtient donc
\(\dfrac{\pi}{12}=\dfrac{180\pi}{12\pi}^\circ=\dfrac{180}{12}^\circ=15^\circ\);
\(\dfrac{2\pi}{3}=\dfrac{180\cdot 2\pi}{3\pi}^\circ=\dfrac{360}{3}^\circ=120^\circ\);
\(-\dfrac{\pi}{4}=\dfrac{7\pi}{4}=\dfrac{180\cdot 7\pi}{4\pi}^\circ=\dfrac{1260}{4}^\circ=315^\circ\).
-
Si \(\sin\theta=\frac{3}{5}\) alors déterminer les autres nombres trigonométriques.
Solution détaillée : On peut représenter la situation à l'aide du triangle rectangle suivant.
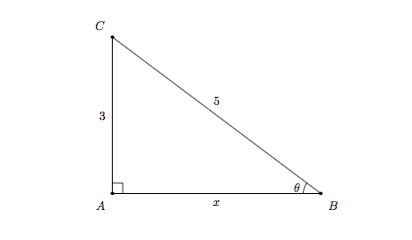
On déduit du Théorème de Pythagore que \(9+x^2=25\), donc \(x^2=16\) et \(x=4\). On obtient alors
\(\cos{\theta}=\frac{\mbox{adjacent}}{\mbox{hypoténuse}}=\dfrac{x}{5}=\dfrac{4}{5}\);
\(\tan{\theta}=\frac{\mbox{opposé}}{\mbox{adjacent}}=\dfrac{3}{x}=\dfrac{3}{4}\);
\(\cot{\theta}=\frac{\mbox{adjacent}}{\mbox{opposé}}=\dfrac{x}{3}=\dfrac{4}{3}\).
-
Sans utiliser de calculatrice, donner la valeur de \(\cos{\frac{5\pi}{6}} et \sin{315^{\circ}}\).
Solution détaillée : On a \(\frac{5\pi}{6}=\pi-\frac{\pi}{6}\) et \(\cos{(\pi-x)}=-\cos{x}\). On en déduit que
\(\cos{\frac{5\pi}{6}}=\cos{(\pi-\frac{\pi}{6})}=-\cos{\frac{\pi}{6}}=-\frac{\sqrt{3}}{2}\).
On a \(315^{\circ}=\frac{7\pi}{4}=2\pi-\frac{\pi}{4}\) et \(\sin{(2\pi-x)}=-\sin{x}\). On en déduit que
\(\sin{\frac{7\pi}{4}}=\sin{(2\pi-\frac{\pi}{4})}=-\sin{\frac{\pi}{4}}=-\frac{\sqrt{2}}{2}\).
-
Résoudre l'équation \(\cos{(3x+\pi)}=\cos{x}\).
Solution détaillée : Pour que deux angles aient le même cosinus, ils doivent être égaux ou opposés (à \(2k\pi\) près). On a donc
\(\begin{array}{lcl} 3x+\pi=x+2k\pi&\mbox{ ou }&3x+\pi=-x+2k\pi\\ 2x=-\pi+2k\pi&\mbox{ ou }&4x=-\pi+2k\pi\\ x=-\dfrac{\pi}{2}+k\pi&\mbox{ ou }&x=-\dfrac{\pi}{4}+k\dfrac{\pi}{2} \end{array}\)
La solution est donc donnée par \(S=\{-\frac{\pi}{2}+k\pi,\, -\frac{\pi}{4}+k\frac{\pi}{2};\, k\in\mathbb{Z}\}\).
-
Résoudre l'équation \(\sin{(\frac{x}{2})}+\cos{x}=1\).
Solution détaillée : En utilisant les formules de duplication, l'équation peut s'écrire
\(\sin{\left( \frac{x}{2}\right) }+1-2\sin^2{\left( \frac{x}{2}\right) }=1\)
ou encore
\(\sin{\left( \frac{x}{2}\right) }\left( 1-2\sin{\left( \frac{x}{2}\right) }\right) =0.\)
On en déduit que \(\sin{(\frac{x}{2})}=0\) ou \(1-2\sin{(\frac{x}{2})}=0\).
D'une part, \(\sin{(\frac{x}{2})}=0\) implique \(\frac{x}{2}=k\pi\) et donc \(x=2k\pi\).
D'autre part, \(1-2\sin{(\frac{x}{2})}=0\) implique \(\sin{(\frac{x}{2})}=\frac{1}{2}\). On en déduit
\(\begin{array}{lcl} \dfrac{x}{2}=\dfrac{\pi}{6}+2k\pi&\mbox{ ou }&\dfrac{x}{2}=\dfrac{5\pi}{6}+2k\pi\\ x=\dfrac{\pi}{3}+4k\pi&\mbox{ ou }&x=\dfrac{5\pi}{3}+4k\pi \end{array} \)
La solution est donc donnée par \(S=\{2k\pi,\, \frac{\pi}{3}+4k\pi,\, \frac{5\pi}{3}+4k\pi;\, k\in\mathbb{Z}\}\).
-
Résoudre l'équation \(\cos{x}+\cos{2x}=0\).
Solution détaillée : En utilisant les formules de duplication, l'équation peut s'écrire
\(2\cos^2{x}+\cos{x}-1=0.\)
Posons \(t=\cos{x}\). L'équation s'écrit alors \(2t^2+t-1=0\). Les solutions de cette équations sont \(t=\frac{1}{2}\) et \(t=-1\) (pour plus de détails concernant la résolution des équations du second degré, cliquez ici.
On en déduit que \(t=\cos{x}=\frac{1}{2}\) ou \(t=\cos{x}=-1\).
D'une part, \(\cos{x}=\frac{1}{2}\) implique \(x=\frac{\pi}{3}+2k\pi\) ou \(x=\frac{5\pi}{3}+2k\pi\).
D'autre part, \(\cos{x}=-1\) implique \(x=\pi+2k\pi\).
La solution est donc donnée par \(S=\{\frac{\pi}{3}+2k\pi,\, \frac{5\pi}{3}+2k\pi,\, \pi+2k\pi;\, k\in\mathbb{Z}\}\).

-
Résoudre l'équation \(\cos{x}+\sin{x}=1\).
Solution détaillée : Puisque \(\sin{x}=\cos{(\frac{\pi}{2}-x)}\), cette équation peut encore s'écrire
\(\cos{x}+\cos{(\frac{\pi}{2}-x)}=1. \)
En utilisant les formules de Simpson, on obtient
\(2\cos{\left( \frac{x+(\frac{\pi}{2}-x)}{2}\right) }\, \cos{\left( \frac{x-(\frac{\pi}{2}-x)}{2}\right) }=1\)
ou encore
\(2\cos{\frac{\pi}{4}}\, \cos{\left( x-\frac{\pi}{4}\right) }=1\)
et comme \(\cos{\frac{\pi}{4}}=\frac{\sqrt{2}}{2}\), l'équation devient \(\sqrt{2}\cos{(x-\frac{\pi}{4})}=1\) d'où \(\cos{(x-\frac{\pi}{4})}=\frac{\sqrt{2}}{2}\). On en déduit que
\(\begin{array}{lcl} x-\dfrac{\pi}{4}=\dfrac{\pi}{4}+2k\pi&\mbox{ ou }&x-\dfrac{\pi}{4}=-\dfrac{\pi}{4}+2k\pi\\ x=\dfrac{\pi}{2}+2k\pi&\mbox{ ou }&x=2k\pi \end{array}\)
La solution est donc donnée par \(S=\{2k\pi,\, \frac{\pi}{2}+2k\pi;\, k\in\mathbb{Z}\}\).
-
A l'aide des formules, calculer \(\sin{\frac{5\pi}{12}}\) et \(\cos{\frac{\pi}{12}}\).
Solution détaillée : Remarquons que \(\frac{5\pi}{12}=\frac{\pi}{4}+\frac{\pi}{6}\) et \(\frac{\pi}{12}=\frac{\pi}{3}-\frac{\pi}{4}\). En utilisant les formules d'addition, on obtient
\(\sin{\frac{5\pi}{12}}=\sin{(\frac{\pi}{4}+\frac{\pi}{6})}=\sin{\frac{\pi}{4}}\cos{\frac{\pi}{6}}+\sin{\frac{\pi}{6}}\cos{\frac{\pi}{4}}=\frac{\sqrt{2}}{2}\cdot\frac{\sqrt{3}}{2}+\frac{1}{2}\cdot\frac{\sqrt{2}}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}.\)
De même,
\(\cos{\frac{\pi}{12}}=\cos{(\frac{\pi}{3}-\frac{\pi}{4})}=\cos{\frac{\pi}{3}}\cos{\frac{\pi}{4}}+\sin{\frac{\pi}{3}}\sin{\frac{\pi}{4}}=\frac{1}{2}\cdot\frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{2}}{2}=\frac{\sqrt{2}+\sqrt{6}}{4}.\)
-
A partir d'un point \(A\) situé \(8\) mètres au-dessus du sol, l'angle d'élévation du sommet d'un bâtiment est de \(30^{\circ}\) et l'angle de dépression de la base du bâtiment est de \(15^{\circ}\). Calculer la hauteur du bâtiment.
Solution détaillée : Le problème est représenté par le schéma suivant
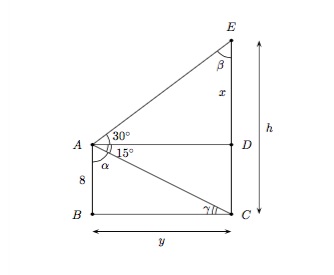
Données : Les angles \(30^{\circ}\) et \(15^{\circ}\) et la longueur du côté \(AB\) (=\(8\) mètres).
Inconnue : La hauteur \(h=x+8\).
Commençons par rechercher les angles : \(\alpha=90^{\circ}-15^{\circ}=75^{\circ}\) (angles complémentaires), \(\beta=90^{\circ}-30^{\circ}=60^{\circ}\) (somme des angles intérieurs d'un triangle) et \(\gamma=15^{\circ}\) (angles alternes-internes).
Déterminons \(y\) dans le triangle rectangle \(ABC\). On a \(\tan\alpha=\frac{\mbox{opposé}}{\mbox{adjacent}}\) et donc \(\tan{75^{\circ}}=\frac{y}{8}\). On en déduit \(y=8\, \tan{75^{\circ}}\).
Déterminons \(x\) dans le triangle rectangle \(ADE\). On a \(\tan{30^{\circ}}=\frac{x}{y}\). On en déduit \(x=y\, \tan{30^{\circ}}\) et donc \(x=8\, \tan{75^{\circ}}\, \tan{30^{\circ}}\).
Finalement, en utilisant les formules d'addition, on a
\(\tan{75^{\circ}}=\tan{(45^{\circ}+30^{\circ})}=\dfrac{\tan{45^{\circ}}+\tan{30^{\circ}}}{1-\tan{45^{\circ}}\, \tan{30^{\circ}}}=\dfrac{1+\frac{\sqrt{3}}{3}}{1-\frac{\sqrt{3}}{3}}=\dfrac{3+\sqrt{3}}{3-\sqrt{3}}.\)
On en déduit que \(x=8\cdot\frac{3+\sqrt{3}}{3-\sqrt{3}}\cdot\frac{\sqrt{3}}{3}=17,24\) et donc la hauteur du bâtiment est \(h=x+8=17,24+8=25,24\) mètres.
-
A l'origine, la Tour de Pise était perpendiculaire à la surface du sol et mesurait 54 mètres de haut. Comme elle s'enfonce dans le sol, elle penche maintenant d'un angle \(\alpha\) par rapport à la perpendiculaire. Lorsque le sommet de la tour est observé à partir d'un point distant de 45 mètres du centre de sa base, l'angle d'élévation est de \(53^\circ\). Calculer l'angle \(\alpha\) et la distance \(d\) qui exprime de combien le centre du sommet de la tour s'est éloigné de la perpendiculaire.
Solution détaillée : Le problème est représenté par le schéma suivant
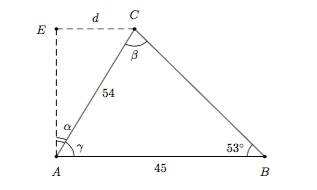
Données : L'angle \(53^{\circ}\) et les longueurs des côtés \(AC\) (=\(54\) mètres) et \(AB\) (=\(45\) mètres).
Inconnue : L'angle \(\alpha\) et la distance \(d\).
Commençons par déterminer l'angle \(\alpha\). En utilisant la Règle des sinus dans le triangle \(ABC\), on obtient
\(\dfrac{\sin{\beta}}{45}=\dfrac{\sin{53^{\circ}}}{54}\)
et donc \(\sin\beta=\frac{45}{54}\, \sin{53^{\circ}}\). On en déduit que \(\beta\simeq 41,72^{\circ}\), \(\gamma=180^{\circ}-53^{\circ}-\beta\simeq 85,28^{\circ}\) et \(\alpha=90^{\circ}-\gamma\simeq 4,72^{\circ}\).
Finalement, on trouve \(d\) dans le triangle rectangle \(ACE\) : \(\sin\alpha=\frac{d}{54}\) et donc
\(d=54\sin\alpha\simeq 4,44\mbox{ mètres}.\)
-
Un poteau haut de 12 mètres est planté sur le flanc d'une colline qui forme un angle de \(17^{\circ}\) avec l'horizontale. Calculez la longueur minimale d'un câble tendu entre le sommet du poteau et un point en contrebas distant de 21,6 mètres de la base du poteau.
Solution détaillée : Le problème est représenté par le schéma suivant
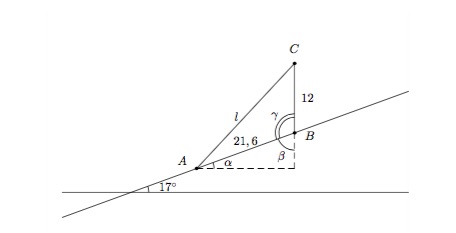
Données : L'angle \(17^{\circ}\), les longueurs des côtés \(AB\) (=\(21,6\) mètres) et \(BC\) (=\(12\) mètres).
Inconnue : La longueur \(l\).
Commençons par déterminer les angles : \(\alpha=17^{\circ}\) (angles correspondants), \(\beta=90^{\circ}-17^{\circ}=73^{\circ}\) (somme des angles intérieurs d'un triangle), \(\gamma=180^ {\circ}-\beta=107^ {\circ}\) (angles supplémentaires).
Déterminons \(l\) en utilisant la Règle des cosinus dans le triangle \(ABC\). On a
\(l^2=(21,6)^2+12^2-2\cdot 21,6\cdot 12\cdot \cos{107^{\circ}}\simeq 762,125\)
et \(l\simeq 27,607\) mètres.
Preuves
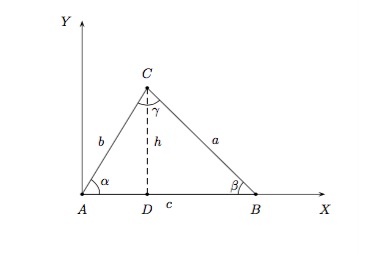
Pour un triangle quelconque \(ABC\), plaçons \(A\) en l'origine et \(B\) sur la partie positive de l'axe \(OX\). Le point \(C\) est donc au-dessus de l'axe \(OX\). Traçons la hauteur \(h\) perpendiculaire à \(c\). Elle coupe le côté \(c\) au point \(D\).
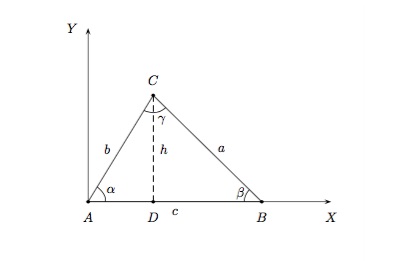
Par la définition des nombres trigonométriques, on a dans le triangle \(ADC\) \(h = b.\sin \alpha\) et dans le triangle \(BDC\) \(h = a.\sin \beta,\)
Dans un cercle, des angles inscrits interceptant le même arc ont même amplitude.
Soit \(\widehat{ACB}\) et \(\widehat{ADB}\) deux angles inscrits dans un cercle et qui interceptent le même arc \(AB\). Soit \(\widehat{AOB}\) l'angle au centre interceptant le même arc \(AB\).
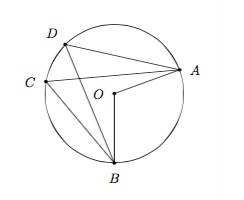
Puisque l'amplitude de l'angle au centre vaut le double de l'amplitude de l'angle inscrit qui intercepte le même arc, on a \(\widehat{AOB}=2\widehat{ACB}\) et \(\widehat{AOB}=2\widehat{ADB}\). Donc \(\widehat{ACB}=\widehat{ADB}\).
Tout triangle inscrit dans un demi-cercle est un triangle rectangle.
Réciproquement, on peut inscrire tout triangle rectangle dans un demi-cercle dont le diamètre est l'hypoténuse du triangle.
Soit \(ABC\) le triangle inscrit dans le demi-cercle de centre \(O\) et de diamètre \(BC\).
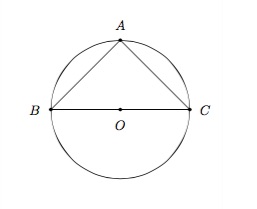
L'angle inscrit \(\widehat{BAC}\) et l'angle au centre \(\widehat{BOC}\) interceptent le même arc \(BC\). Puisque l'amplitude de l'angle au centre vaut le double de l'amplitude de l'angle inscrit qui intercepte le même arc, on a \(\widehat{BOC}=2\widehat{BAC}\). Comme \(\widehat{BOC}=180^{\circ}\), on a \(\widehat{BAC}=90^{\circ}\) et le triangle \(ABC\) est rectangle en \(A\).
Réciproquement, soit \(ABC\) un triangle rectangle en \(A\) et \(O\) le point milieu du segment \(BC\).
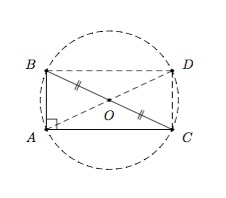
Traçons le cercle de centre \(O\) et de diamètre \(BC\) ainsi que le rectangle \(ABDC\). Dans un rectangle, les diagonales ont même longueur et se coupent en leur milieu. On en déduit que \(\vert AO\vert=\vert OD\vert=\vert BO\vert=\vert OC\vert\). Donc \(A\) appartient au cercle de centre \(O\) et de diamètre \(BC\).
Dans un cercle, l'amplitude de l'angle au centre vaut le double de l'amplitude de l'angle inscrit qui intercepte le même arc.
Soit \(O\) le centre du cercle, \(\widehat{AOB}\) l'angle au centre interceptant l'arc \(AB\) et \(\widehat{BCA}\) l'angle inscrit interceptant l'arc \(AB\).
Cas 1 : Le centre appartient à un côté de l'angle inscrit.
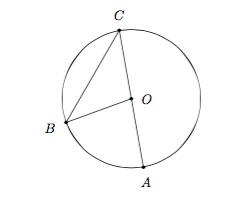
On a \(\widehat{AOB}+\widehat{COB}=180^{\circ}\) mais aussi \(\widehat{OBC}+\widehat{BCO}+\widehat{COB}=180^{\circ}\). On en déduit que \(\widehat{AOB}=\widehat{OBC}+\widehat{BCO}\).
Puisque \(\vert OB\vert=\vert OC\vert\) est le rayon du cercle, le triangle \(COB\) est isocèle et donc \(\widehat{OBC}=\widehat{BCO}\). Finalement, on a
\(\widehat{AOB}=\widehat{OBC}+\widehat{BCO}=2\widehat{BCO}=2\widehat{BCA}.\)
Cas 2 : Le centre est intérieur à l'angle inscrit.
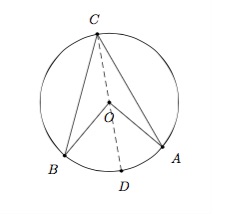
Traçons le diamètre \(CD\). On déduit du Cas 1 que \(\widehat{BOD}=2\widehat{BCD}\) et \(\widehat{DOA}=2\widehat{DCA}\). Donc
\(\widehat{BOA}=\widehat{BOD}+\widehat{DOA}=2\widehat{BCD}+2\widehat{DCA}=2(\widehat{BCD}+\widehat{DCA})=2\widehat{BCA}.\)
Cas 3 : Le centre est extérieur à l'angle inscrit.
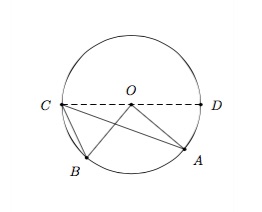
Traçons le diamètre \(CD\). On déduit du Cas 1 que \(\widehat{BOD}=2\widehat{BCD}\) et \(\widehat{AOD}=2\widehat{ACD}\). Donc
\(\widehat{BOA}=\widehat{BOD}-\widehat{AOD}=2\widehat{BCD}-2\widehat{ACD}=2(\widehat{BCD}-\widehat{ACD})=2\widehat{BCA}.\)
