Théorie du module : Trigonométrie

Table des matières

Preuves

Règle des sinus : Dans tout triangle, les longueurs des côtés sont proportionnelles aux sinus des angles opposés, c'est-à-dire si \(a\), \(b\) et \(c\) sont les côtés d'un triangle et \(\alpha\), \(\beta\) et \(\gamma\) sont les angles opposés respectivement à ces côtés, on a \(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}.\)

Pour un triangle quelconque \(ABC\), plaçons \(A\) en l'origine et \(B\) sur la partie positive de l'axe \(OX\). Le point \(C\) est donc au-dessus de l'axe \(OX\). Traçons la hauteur \(h\) perpendiculaire à \(c\). Elle coupe le côté \(c\) au point \(D\).

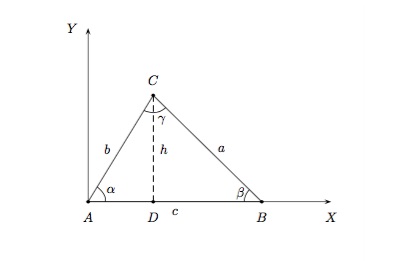
Par la définition des nombres trigonométriques, on a dans le triangle \(ADC\) \(h = b.\sin \alpha\) et dans le triangle \(BDC\) \(h = a.\sin \beta,\)

d'où,

\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}.\)

Par un argument similaire (en plaçant \(A\) en l'origine et \(C\) sur la partie positive de l'axe \(OX\)), on obtient que

\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \gamma}{c}.\)

Règle des cosinus : Dans tout triangle, le carré de la longueur d'un côté est égal à la somme des carrés des longueurs des deux autres côtés diminuée du double produit des longueurs de ces deux côtés par le cosinus de l'angle compris entre ces côtés, c'est-à-dire si \(a\), \(b\) et \(c\) sont les longueurs des côtés d'un triangle et \(\alpha\), \(\beta\) et \(\gamma\) sont les angles opposés respectivement à ces côtés, on a

\(\begin{array}{l} a^2=b^2+c^2-2bc\cos{\alpha} \\ b^2=a^2+c^2-2ac\cos{\beta} \\ c^2=a^2+b^2-2ab\cos{\gamma} \end{array}\)

Dans le triangle rectangle \(BCD\), on déduit du Théorème de Pythagore que

\(\begin{array}{rl} \vert BC\vert^2 & =\vert BD\vert^2+\vert DC\vert^2 \\ & =(\vert AB\vert-\vert DA\vert)^2+\vert DC\vert^2 \\ & =\vert AB\vert^2+\vert DA\vert^2-2\vert AB\vert\cdot\vert DA\vert+\vert DC\vert^2 \\ & =\vert AB\vert^2+(\vert DA\vert^2+\vert DC\vert^2)-2\vert AB\vert\cdot \vert DA\vert \end{array}\)

Dans le triangle rectangle \(ACD\), on a par le Théorème de Pythagore

\(\vert DA\vert^2+\vert DC\vert^2=\vert AC\vert^2\)

et aussi

\(\vert DA\vert=\vert AC\vert\cos{\alpha}.\)

On en déduit

\(\vert BC\vert^2=\vert AB\vert^2+\vert AC\vert^2-2 \vert AB\vert\cdot\vert AC\vert\cos{\alpha}\)

ou encore

\(a^2=c^2+b^2-2bc\cos{\alpha}.\)

Les deux autres égalités s'obtiennent de façon analogue.

Dans un cercle, des angles inscrits interceptant le même arc ont même amplitude.

Soit \(\widehat{ACB}\) et \(\widehat{ADB}\) deux angles inscrits dans un cercle et qui interceptent le même arc \(AB\). Soit \(\widehat{AOB}\) l'angle au centre interceptant le même arc \(AB\).

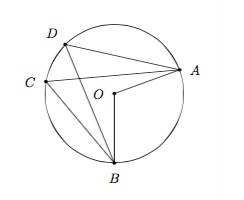
Puisque l'amplitude de l'angle au centre vaut le double de l'amplitude de l'angle inscrit qui intercepte le même arc, on a \(\widehat{AOB}=2\widehat{ACB}\) et \(\widehat{AOB}=2\widehat{ADB}\). Donc \(\widehat{ACB}=\widehat{ADB}\).

Tout triangle inscrit dans un demi-cercle est un triangle rectangle.

Réciproquement, on peut inscrire tout triangle rectangle dans un demi-cercle dont le diamètre est l'hypoténuse du triangle.

Soit \(ABC\) le triangle inscrit dans le demi-cercle de centre \(O\) et de diamètre \(BC\).

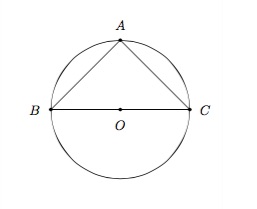
L'angle inscrit \(\widehat{BAC}\) et l'angle au centre \(\widehat{BOC}\) interceptent le même arc \(BC\). Puisque l'amplitude de l'angle au centre vaut le double de l'amplitude de l'angle inscrit qui intercepte le même arc, on a \(\widehat{BOC}=2\widehat{BAC}\). Comme \(\widehat{BOC}=180^{\circ}\), on a \(\widehat{BAC}=90^{\circ}\) et le triangle \(ABC\) est rectangle en \(A\).

Réciproquement, soit \(ABC\) un triangle rectangle en \(A\) et \(O\) le point milieu du segment \(BC\).

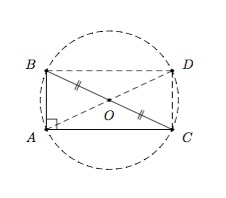
Traçons le cercle de centre \(O\) et de diamètre \(BC\) ainsi que le rectangle \(ABDC\). Dans un rectangle, les diagonales ont même longueur et se coupent en leur milieu. On en déduit que \(\vert AO\vert=\vert OD\vert=\vert BO\vert=\vert OC\vert\). Donc \(A\) appartient au cercle de centre \(O\) et de diamètre \(BC\).

Dans un cercle, l'amplitude de l'angle au centre vaut le double de l'amplitude de l'angle inscrit qui intercepte le même arc.

Soit \(O\) le centre du cercle, \(\widehat{AOB}\) l'angle au centre interceptant l'arc \(AB\) et \(\widehat{BCA}\) l'angle inscrit interceptant l'arc \(AB\).

Cas 1 : Le centre appartient à un côté de l'angle inscrit.

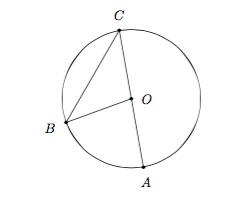
On a \(\widehat{AOB}+\widehat{COB}=180^{\circ}\) mais aussi \(\widehat{OBC}+\widehat{BCO}+\widehat{COB}=180^{\circ}\). On en déduit que \(\widehat{AOB}=\widehat{OBC}+\widehat{BCO}\).

Puisque \(\vert OB\vert=\vert OC\vert\) est le rayon du cercle, le triangle \(COB\) est isocèle et donc \(\widehat{OBC}=\widehat{BCO}\). Finalement, on a

\(\widehat{AOB}=\widehat{OBC}+\widehat{BCO}=2\widehat{BCO}=2\widehat{BCA}.\)

Cas 2 : Le centre est intérieur à l'angle inscrit.

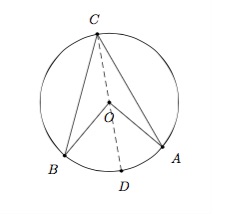
Traçons le diamètre \(CD\). On déduit du Cas 1 que \(\widehat{BOD}=2\widehat{BCD}\) et \(\widehat{DOA}=2\widehat{DCA}\). Donc

\(\widehat{BOA}=\widehat{BOD}+\widehat{DOA}=2\widehat{BCD}+2\widehat{DCA}=2(\widehat{BCD}+\widehat{DCA})=2\widehat{BCA}.\)

Cas 3 : Le centre est extérieur à l'angle inscrit.

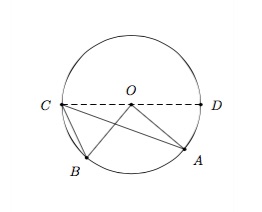
Traçons le diamètre \(CD\). On déduit du Cas 1 que \(\widehat{BOD}=2\widehat{BCD}\) et \(\widehat{AOD}=2\widehat{ACD}\). Donc

\(\widehat{BOA}=\widehat{BOD}-\widehat{AOD}=2\widehat{BCD}-2\widehat{ACD}=2(\widehat{BCD}-\widehat{ACD})=2\widehat{BCA}.\)

Théorie

Retour au module