Théorie du module : Trigonométrie
Table des matières
- Angles
- Nombres trigonométriques
- Règle des sinus et Règle des cosinus
- Equations trigonométriques
- Exemples détaillés
Règle des sinus et Règle des cosinus
Le résultat suivant permet de trouver la longueur d'un côté d'un triangle quelconque si on connaît la longueur d'un autre côté et les deux angles opposés. Il permet également de déterminer un angle si on en connaît un autre et la longueur de leurs côtés opposés.
Règle des sinus - Dans tout triangle, les longueurs des côtés sont proportionnelles aux sinus des angles opposés, c'est-à-dire si \(a\), \(b\) et \(c\) sont les longueurs des côtés d'un triangle et \(\alpha\), \(\beta\) et \(\gamma\) sont les angles opposés respectivement à ces côtés, on a
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}.\)
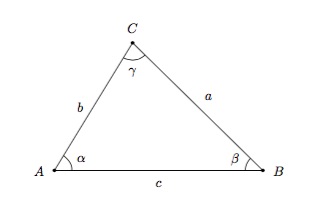
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
Voici un exemple d'application de ce résultat. Lorsque l'angle d'élévation du soleil est de \(64^\circ\), un poteau téléphonique qui penche d'un angle de \(9^\circ\) par rapport à une ligne formée par le pied du poteau et le soleil projette une ombre de 6,3 mètres sur le sol. On cherche la hauteur du poteau.
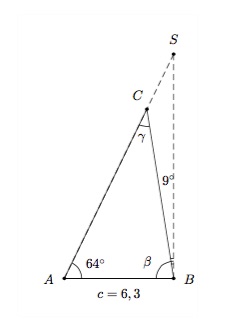
Le triangle \(ABC\) (avec \(\alpha= 64^\circ\), \(\beta =90^\circ - 9^\circ = 81^\circ\) et \(\gamma = 180^\circ- 64^\circ-81^\circ = 35^\circ\)) représente les faits. Pour calculer la hauteur du poteau, c'est-à-dire le côté \(a=BC\) du triangle \(ABC\), on utilise la Règle des sinus :
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \gamma}{c},\)
c'est-à-dire
\(\dfrac{\sin 64^\circ}{a}=\dfrac{\sin 35^\circ}{6,3},\)
d'où \(a=6,3\cdot \frac{\sin 64^\circ}{\sin 35^\circ}=9,87\) mètres.
Le résultat suivant est une généralisation du Théorème de Pythagore. Il permet de trouver la longueur d'un des côtés à partir de celle des deux autres et de l'angle compris entre ces deux autres côtés. Il porte le nom de règle des cosinus ou encore règle de Pythagore généralisée.
Règle des cosinus - Dans tout triangle, le carré de la longueur d'un côté est égal à la somme des carrés des longueurs des deux autres côtés diminuée du double produit des longueurs de ces deux côtés par le cosinus de l'angle compris entre ces côtés, c'est-à-dire si \(a\), \(b\) et \(c\) sont les longueurs des côtés d'un triangle et \(\alpha\), \(\beta\) et \(\gamma\) sont les angles opposés respectivement à ces côtés, on a
\(\begin{array}{l} a^2=b^2+c^2-2bc\cos{\alpha} \\ b^2=a^2+c^2-2ac\cos{\beta} \\ c^2=a^2+b^2-2ab\cos{\gamma} \end{array}\)
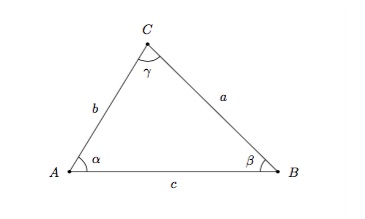
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
Voici un exemple d'application de ce résultat. Sur le flanc d'une montagne se trouve une tour. Un observateur se trouvant à 320 mètres de la tour la voit sous un angle de \(6^{\circ}\). Il monte alors dans la direction de la tour et, après avoir parcouru 220 mètres, il la voit sous un angle de \(13^{\circ}\). On cherche la hauteur de cette tour. Schématisons la situation.
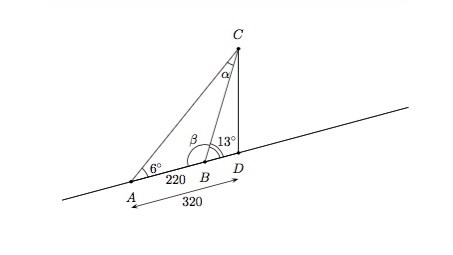
On déduit des données que l'angle \(\beta=180^{\circ}-13^{\circ}=167^{\circ}\), donc l'angle \(\alpha=180^{\circ}-167^{\circ}-6^{\circ}=7^{\circ}\).
On déduit la longueur du côté \(AC\) de la Règle des sinus :
\(\dfrac{220}{\sin{7^{\circ}}}=\dfrac{\vert AC\vert}{\sin{167^{\circ}}}\)
et donc \(\vert AC\vert=220\cdot \dfrac{\sin{167^{\circ}}}{\sin{7^{\circ}}}=406,1\) mètres.
Finalement, par la Règle des cosinus, on obtient
\(\begin{array}{rcl} h^2=\vert CD\vert^2 &= &\vert AD\vert^2+\vert AC\vert^2-2\vert AD\vert\, \vert AC\vert\, \cos{6^{\circ}} \\ & = &320^2+\left( 220\cdot \dfrac{\sin{167^{\circ}}}{\sin{7^{\circ}}}\right)^2 -2\cdot 320\cdot \left( 220\cdot \dfrac{\sin{167^{\circ}}}{\sin{7^{\circ}}}\right) \cdot\cos{6^{\circ}} \\ & = &8836,99 \end{array}\)
et donc \(h=\sqrt{h^2}\approx 94\) mètres.
