Théorie du module : Trigonométrie
Table des matières
- Angles
- Nombres trigonométriques
- Règle des sinus et Règle des cosinus
- Equations trigonométriques
- Exemples détaillés
Exemples détaillés
-
Convertir les angles \(150^{\circ}\), \(-135^{\circ}\) et \(390^{\circ}\) en radians.
Solution détaillée : La formule permettant de passer de degrés en radians est
\(1\mbox{ degré }= \dfrac{2 \pi }{360}\mbox{ radians }= \dfrac{\pi }{180}\mbox{ radians}.\)
On obtient donc
\(150^{\circ}=150\cdot\dfrac{\pi }{180}\mbox{ radians }=\dfrac{5\pi}{6}\mbox{ radians}\);
\(-135^{\circ}=-135\cdot\dfrac{\pi }{180}\mbox{ radians }=-\dfrac{3\pi}{4}\mbox{ radians }=\dfrac{5\pi}{4}\mbox{ radians}\);
\(390^{\circ}=30^{\circ}=30\cdot\dfrac{\pi }{180}\mbox{ radians }=\dfrac{\pi}{6}\mbox{ radians}\).
-
Convertir en degrés les angles \(\dfrac{\pi}{12}\), \(\dfrac{2\pi}{3}\) et \(-\dfrac{\pi}{4}\).
Solution détaillée : La formule permettant de passer de radians en degrés est
\(1\mbox{ radian } = \dfrac{360^\circ}{2 \pi}= \dfrac{180^\circ}{\pi}.\)
On obtient donc
\(\dfrac{\pi}{12}=\dfrac{180\pi}{12\pi}^\circ=\dfrac{180}{12}^\circ=15^\circ\);
\(\dfrac{2\pi}{3}=\dfrac{180\cdot 2\pi}{3\pi}^\circ=\dfrac{360}{3}^\circ=120^\circ\);
\(-\dfrac{\pi}{4}=\dfrac{7\pi}{4}=\dfrac{180\cdot 7\pi}{4\pi}^\circ=\dfrac{1260}{4}^\circ=315^\circ\).
-
Si \(\sin\theta=\frac{3}{5}\) alors déterminer les autres nombres trigonométriques.
Solution détaillée : On peut représenter la situation à l'aide du triangle rectangle suivant.
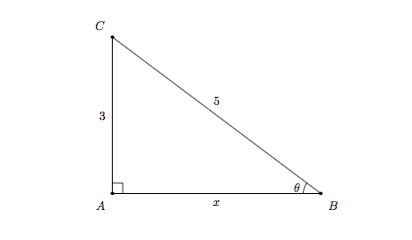
On déduit du Théorème de Pythagore que \(9+x^2=25\), donc \(x^2=16\) et \(x=4\). On obtient alors
\(\cos{\theta}=\frac{\mbox{adjacent}}{\mbox{hypoténuse}}=\dfrac{x}{5}=\dfrac{4}{5}\);
\(\tan{\theta}=\frac{\mbox{opposé}}{\mbox{adjacent}}=\dfrac{3}{x}=\dfrac{3}{4}\);
\(\cot{\theta}=\frac{\mbox{adjacent}}{\mbox{opposé}}=\dfrac{x}{3}=\dfrac{4}{3}\).
-
Sans utiliser de calculatrice, donner la valeur de \(\cos{\frac{5\pi}{6}} et \sin{315^{\circ}}\).
Solution détaillée : On a \(\frac{5\pi}{6}=\pi-\frac{\pi}{6}\) et \(\cos{(\pi-x)}=-\cos{x}\). On en déduit que
\(\cos{\frac{5\pi}{6}}=\cos{(\pi-\frac{\pi}{6})}=-\cos{\frac{\pi}{6}}=-\frac{\sqrt{3}}{2}\).
On a \(315^{\circ}=\frac{7\pi}{4}=2\pi-\frac{\pi}{4}\) et \(\sin{(2\pi-x)}=-\sin{x}\). On en déduit que
\(\sin{\frac{7\pi}{4}}=\sin{(2\pi-\frac{\pi}{4})}=-\sin{\frac{\pi}{4}}=-\frac{\sqrt{2}}{2}\).
-
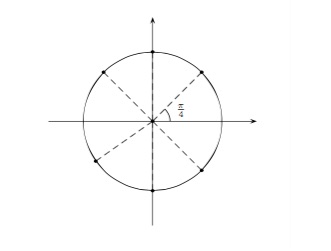
Résoudre l'équation \(\cos{(3x+\pi)}=\cos{x}\).
Solution détaillée : Pour que deux angles aient le même cosinus, ils doivent être égaux ou opposés (à \(2k\pi\) près). On a donc
\(\begin{array}{lcl} 3x+\pi=x+2k\pi&\mbox{ ou }&3x+\pi=-x+2k\pi\\ 2x=-\pi+2k\pi&\mbox{ ou }&4x=-\pi+2k\pi\\ x=-\dfrac{\pi}{2}+k\pi&\mbox{ ou }&x=-\dfrac{\pi}{4}+k\dfrac{\pi}{2} \end{array}\)
La solution est donc donnée par \(S=\{-\frac{\pi}{2}+k\pi,\, -\frac{\pi}{4}+k\frac{\pi}{2};\, k\in\mathbb{Z}\}\).
-
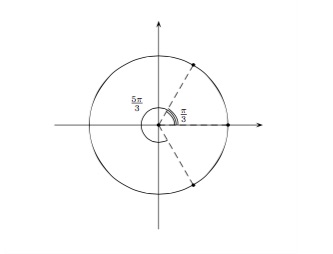
Résoudre l'équation \(\sin{(\frac{x}{2})}+\cos{x}=1\).
Solution détaillée : En utilisant les formules de duplication, l'équation peut s'écrire
\(\sin{\left( \frac{x}{2}\right) }+1-2\sin^2{\left( \frac{x}{2}\right) }=1\)
ou encore
\(\sin{\left( \frac{x}{2}\right) }\left( 1-2\sin{\left( \frac{x}{2}\right) }\right) =0.\)
On en déduit que \(\sin{(\frac{x}{2})}=0\) ou \(1-2\sin{(\frac{x}{2})}=0\).
D'une part, \(\sin{(\frac{x}{2})}=0\) implique \(\frac{x}{2}=k\pi\) et donc \(x=2k\pi\).
D'autre part, \(1-2\sin{(\frac{x}{2})}=0\) implique \(\sin{(\frac{x}{2})}=\frac{1}{2}\). On en déduit
\(\begin{array}{lcl} \dfrac{x}{2}=\dfrac{\pi}{6}+2k\pi&\mbox{ ou }&\dfrac{x}{2}=\dfrac{5\pi}{6}+2k\pi\\ x=\dfrac{\pi}{3}+4k\pi&\mbox{ ou }&x=\dfrac{5\pi}{3}+4k\pi \end{array} \)
La solution est donc donnée par \(S=\{2k\pi,\, \frac{\pi}{3}+4k\pi,\, \frac{5\pi}{3}+4k\pi;\, k\in\mathbb{Z}\}\).
-
Résoudre l'équation \(\cos{x}+\cos{2x}=0\).
Solution détaillée : En utilisant les formules de duplication, l'équation peut s'écrire
\(2\cos^2{x}+\cos{x}-1=0.\)
Posons \(t=\cos{x}\). L'équation s'écrit alors \(2t^2+t-1=0\). Les solutions de cette équations sont \(t=\frac{1}{2}\) et \(t=-1\) (pour plus de détails concernant la résolution des équations du second degré, cliquez ici.
On en déduit que \(t=\cos{x}=\frac{1}{2}\) ou \(t=\cos{x}=-1\).
D'une part, \(\cos{x}=\frac{1}{2}\) implique \(x=\frac{\pi}{3}+2k\pi\) ou \(x=\frac{5\pi}{3}+2k\pi\).
D'autre part, \(\cos{x}=-1\) implique \(x=\pi+2k\pi\).
La solution est donc donnée par \(S=\{\frac{\pi}{3}+2k\pi,\, \frac{5\pi}{3}+2k\pi,\, \pi+2k\pi;\, k\in\mathbb{Z}\}\).

-
Résoudre l'équation \(\cos{x}+\sin{x}=1\).
Solution détaillée : Puisque \(\sin{x}=\cos{(\frac{\pi}{2}-x)}\), cette équation peut encore s'écrire
\(\cos{x}+\cos{(\frac{\pi}{2}-x)}=1. \)
En utilisant les formules de Simpson, on obtient
\(2\cos{\left( \frac{x+(\frac{\pi}{2}-x)}{2}\right) }\, \cos{\left( \frac{x-(\frac{\pi}{2}-x)}{2}\right) }=1\)
ou encore
\(2\cos{\frac{\pi}{4}}\, \cos{\left( x-\frac{\pi}{4}\right) }=1\)
et comme \(\cos{\frac{\pi}{4}}=\frac{\sqrt{2}}{2}\), l'équation devient \(\sqrt{2}\cos{(x-\frac{\pi}{4})}=1\) d'où \(\cos{(x-\frac{\pi}{4})}=\frac{\sqrt{2}}{2}\). On en déduit que
\(\begin{array}{lcl} x-\dfrac{\pi}{4}=\dfrac{\pi}{4}+2k\pi&\mbox{ ou }&x-\dfrac{\pi}{4}=-\dfrac{\pi}{4}+2k\pi\\ x=\dfrac{\pi}{2}+2k\pi&\mbox{ ou }&x=2k\pi \end{array}\)
La solution est donc donnée par \(S=\{2k\pi,\, \frac{\pi}{2}+2k\pi;\, k\in\mathbb{Z}\}\).
-
A l'aide des formules, calculer \(\sin{\frac{5\pi}{12}}\) et \(\cos{\frac{\pi}{12}}\).
Solution détaillée : Remarquons que \(\frac{5\pi}{12}=\frac{\pi}{4}+\frac{\pi}{6}\) et \(\frac{\pi}{12}=\frac{\pi}{3}-\frac{\pi}{4}\). En utilisant les formules d'addition, on obtient
\(\sin{\frac{5\pi}{12}}=\sin{(\frac{\pi}{4}+\frac{\pi}{6})}=\sin{\frac{\pi}{4}}\cos{\frac{\pi}{6}}+\sin{\frac{\pi}{6}}\cos{\frac{\pi}{4}}=\frac{\sqrt{2}}{2}\cdot\frac{\sqrt{3}}{2}+\frac{1}{2}\cdot\frac{\sqrt{2}}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}.\)
De même,
\(\cos{\frac{\pi}{12}}=\cos{(\frac{\pi}{3}-\frac{\pi}{4})}=\cos{\frac{\pi}{3}}\cos{\frac{\pi}{4}}+\sin{\frac{\pi}{3}}\sin{\frac{\pi}{4}}=\frac{1}{2}\cdot\frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{2}}{2}=\frac{\sqrt{2}+\sqrt{6}}{4}.\)
-
A partir d'un point \(A\) situé \(8\) mètres au-dessus du sol, l'angle d'élévation du sommet d'un bâtiment est de \(30^{\circ}\) et l'angle de dépression de la base du bâtiment est de \(15^{\circ}\). Calculer la hauteur du bâtiment.
Solution détaillée : Le problème est représenté par le schéma suivant
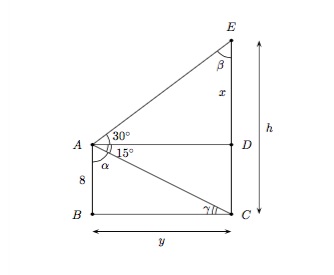
Données : Les angles \(30^{\circ}\) et \(15^{\circ}\) et la longueur du côté \(AB\) (=\(8\) mètres).
Inconnue : La hauteur \(h=x+8\).
Commençons par rechercher les angles : \(\alpha=90^{\circ}-15^{\circ}=75^{\circ}\) (angles complémentaires), \(\beta=90^{\circ}-30^{\circ}=60^{\circ}\) (somme des angles intérieurs d'un triangle) et \(\gamma=15^{\circ}\) (angles alternes-internes).
Déterminons \(y\) dans le triangle rectangle \(ABC\). On a \(\tan\alpha=\frac{\mbox{opposé}}{\mbox{adjacent}}\) et donc \(\tan{75^{\circ}}=\frac{y}{8}\). On en déduit \(y=8\, \tan{75^{\circ}}\).
Déterminons \(x\) dans le triangle rectangle \(ADE\). On a \(\tan{30^{\circ}}=\frac{x}{y}\). On en déduit \(x=y\, \tan{30^{\circ}}\) et donc \(x=8\, \tan{75^{\circ}}\, \tan{30^{\circ}}\).
Finalement, en utilisant les formules d'addition, on a
\(\tan{75^{\circ}}=\tan{(45^{\circ}+30^{\circ})}=\dfrac{\tan{45^{\circ}}+\tan{30^{\circ}}}{1-\tan{45^{\circ}}\, \tan{30^{\circ}}}=\dfrac{1+\frac{\sqrt{3}}{3}}{1-\frac{\sqrt{3}}{3}}=\dfrac{3+\sqrt{3}}{3-\sqrt{3}}.\)
On en déduit que \(x=8\cdot\frac{3+\sqrt{3}}{3-\sqrt{3}}\cdot\frac{\sqrt{3}}{3}=17,24\) et donc la hauteur du bâtiment est \(h=x+8=17,24+8=25,24\) mètres.
-
A l'origine, la Tour de Pise était perpendiculaire à la surface du sol et mesurait 54 mètres de haut. Comme elle s'enfonce dans le sol, elle penche maintenant d'un angle \(\alpha\) par rapport à la perpendiculaire. Lorsque le sommet de la tour est observé à partir d'un point distant de 45 mètres du centre de sa base, l'angle d'élévation est de \(53^\circ\). Calculer l'angle \(\alpha\) et la distance \(d\) qui exprime de combien le centre du sommet de la tour s'est éloigné de la perpendiculaire.
Solution détaillée : Le problème est représenté par le schéma suivant
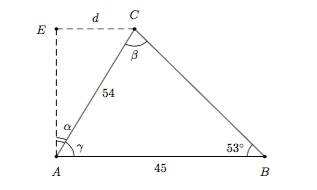
Données : L'angle \(53^{\circ}\) et les longueurs des côtés \(AC\) (=\(54\) mètres) et \(AB\) (=\(45\) mètres).
Inconnue : L'angle \(\alpha\) et la distance \(d\).
Commençons par déterminer l'angle \(\alpha\). En utilisant la Règle des sinus dans le triangle \(ABC\), on obtient
\(\dfrac{\sin{\beta}}{45}=\dfrac{\sin{53^{\circ}}}{54}\)
et donc \(\sin\beta=\frac{45}{54}\, \sin{53^{\circ}}\). On en déduit que \(\beta\simeq 41,72^{\circ}\), \(\gamma=180^{\circ}-53^{\circ}-\beta\simeq 85,28^{\circ}\) et \(\alpha=90^{\circ}-\gamma\simeq 4,72^{\circ}\).
Finalement, on trouve \(d\) dans le triangle rectangle \(ACE\) : \(\sin\alpha=\frac{d}{54}\) et donc
\(d=54\sin\alpha\simeq 4,44\mbox{ mètres}.\)
-
Un poteau haut de 12 mètres est planté sur le flanc d'une colline qui forme un angle de \(17^{\circ}\) avec l'horizontale. Calculez la longueur minimale d'un câble tendu entre le sommet du poteau et un point en contrebas distant de 21,6 mètres de la base du poteau.
Solution détaillée : Le problème est représenté par le schéma suivant
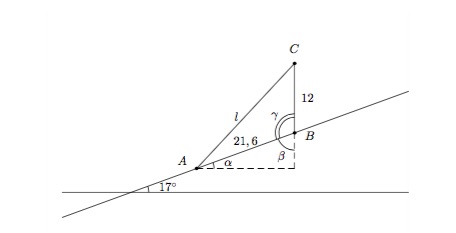
Données : L'angle \(17^{\circ}\), les longueurs des côtés \(AB\) (=\(21,6\) mètres) et \(BC\) (=\(12\) mètres).
Inconnue : La longueur \(l\).
Commençons par déterminer les angles : \(\alpha=17^{\circ}\) (angles correspondants), \(\beta=90^{\circ}-17^{\circ}=73^{\circ}\) (somme des angles intérieurs d'un triangle), \(\gamma=180^ {\circ}-\beta=107^ {\circ}\) (angles supplémentaires).
Déterminons \(l\) en utilisant la Règle des cosinus dans le triangle \(ABC\). On a
\(l^2=(21,6)^2+12^2-2\cdot 21,6\cdot 12\cdot \cos{107^{\circ}}\simeq 762,125\)
et \(l\simeq 27,607\) mètres.
