Théorie du module : Fonctions
Table des matières
- Définitions
- Représentation graphique
- Propriétés
- Fonctions élémentaires
- Opérations sur les fonctions
- Exemples détaillés
Fonctions élémentaires
(a) Fonction constante
La fonction constante \(f(x)=c\) est définie sur \(\mathbb{R}\) et son ensemble image est réduit au seul nombre \(c\). Son graphique est une droite horizontale.
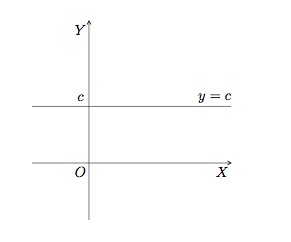
(b) Fonction identité
La fonction identité \(f(x)=x\) est définie sur \(\mathbb{R}\) et son ensemble image est \(\mathbb{R}\). Son graphe est constitué de l'ensemble des couples \((x,y)\) où \(y=x\). Comme ces points sont à égale distance des deux axes, ils appartiennent à la bissectrice des axes.
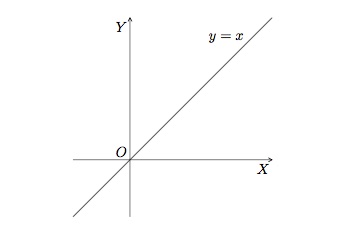
Cette fonction a une racine \(x=0\) et son ordonnée à l'origine est \(y=0\). Elle est positive pour les valeurs de \(x\) positives et négative pour les valeurs de \(x\) négatives. Elle est impaire et strictement croissante sur \(\mathbb{R}\). Elle n'a ni minimum, ni maximum.
(c) Fonction valeur absolue
La fonction valeur absolue \(f(x)=|x|\) est définie sur \(\mathbb{R}\) et son ensemble image est \(\mathbb{R}^+\). Son graphe est constitué de l'ensemble des couples \((x,y)\) où \(y=|x|\).
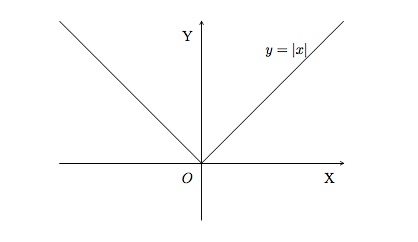
Cette fonction a une racine \(x=0\) et son ordonnée à l'origine est \(y=0\). Elle est toujours positive et nulle en \(0\). Elle est paire et strictement croissante sur \(\mathbb{R}^+\), strictement décroissante sur \(\mathbb{R}^-\). Elle a un minimum en \(x=0\) et pas de maximum.
Cliquez sur le lien pour un rappel des propriétés de la valeur absolue.
(d) Fonctions puissances
Une fonction de la forme \(f(x)=x^{a}\), où \(a\) est une constante, est appelée une fonction puissance. Nous envisageons plusieurs cas.
- \(a=0\). On retrouve la fonction constante \(f(x)=x^0=1\).
- \(a=1\). On retrouve la fonction identité \(f(x)=x\).
- \(a=2\). La fonction du second degré \(f(x)=x^2\) est définie sur \(\mathbb{R}\) et son ensemble image est \(\mathbb{R}^+\). Son graphe est l'ensemble des couples \((x,y)\) où \(y=x^2\).
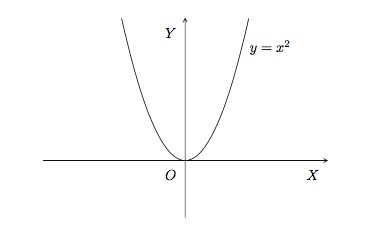
Cette fonction a une racine \(x=0\) et son ordonnée à l'origine est \(y=0\). Elle est toujours positive et nulle en \(0\). Elle est paire et strictement croissante sur \(\mathbb{R}^+\), strictement décroissante sur \(\mathbb{R}^-\). Elle a un minimum en \(x=0\) et pas de maximum.
- \(a=3\). La fonction du troisième degré \(f(x)=x^3\) est définie sur \(\mathbb{R}\) et son ensemble image est \(\mathbb{R}\). Son graphe est l'ensemble des couples \((x,y)\) où \(y=x^3\).
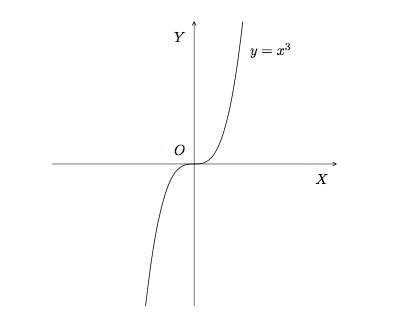
Cette fonction a une racine \(x=0\) et son ordonnée à l'origine est \(y=0\). Elle est positive pour les valeurs de \(x\) positives et négative pour les valeurs de \(x\) négatives. Elle est impaire et strictement croissante sur \(\mathbb{R}\). Elle n'a ni minimum, ni maximum.
- \(a=n\), \(n\in\mathbb{N}_0\). L'allure générale du graphique de \(f(x)=x^n\) change selon que \(n\) est un nombre pair ou impair. Lorsque \(n\) est pair, la fonction \(f(x)=x^n\) est paire et son graphique ressemble à la parabole \(y=x^2\). Lorsque \(n\) est impair, \(f(x)=x^n\) est une fonction impaire et son graphique a la même allure que \(y=x^3\).
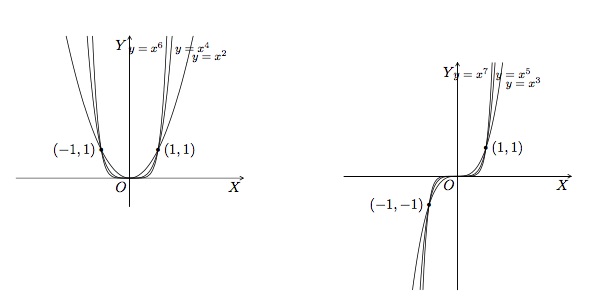
Cliquez sur le lien pour un rappel concernant les propriétés des puissances.
- \(a=-1\). La fonction inverse \(f(x)=\frac{1}{x}\) est définie sur \(\mathbb{R}_0\) et son ensemble image est \(\mathbb{R}_0\) . Son graphe est une hyperbole équilatère dont les axes de coordonnées sont les asymptotes.
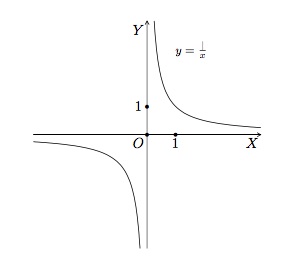
Cette fonction n'a pas de racine ni d'ordonnée à l'origine. Elle est positive pour les valeurs de \(x\) positives et négative pour les valeurs de \(x\) négatives. Elle est impaire et strictement croissante sur \(\mathbb{R}^+_0\), strictement décroissante sur \(\mathbb{R}^-_0\). Elle n'a ni minimum, ni maximum.
- \(a=1/n\), \(n\in\mathbb{N}_0\). La fonction \(f(x)=x^{1/n}=\sqrt[n]x\) est une fonction racine. Lorsque \(n=2\), il s'agit de la fonction racine carrée définie sur \([0;+\infty[\) et dont la courbe représentative est la moitié supérieure de la parabole \(x=y^2\). Lorsque \(n\) est un autre nombre pair, le graphique de \(y=\sqrt[n]x\) est semblable à celui de \(y=\sqrt x\). A la valeur impaire \(n=3\) correspond la fonction racine cubique \(f(x)=\sqrt[3]x\) définie sur \(\mathbb{R}\). Le graphique de \(y=\sqrt[n]x\) pour \(n\) impair (\(n>3\)) ressemble à celui de \(y=\sqrt[3]x\).
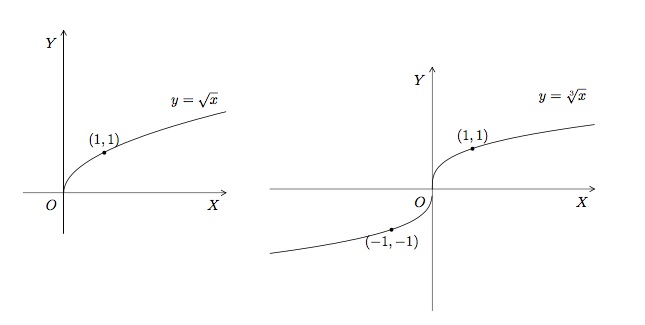
Pour \(n\) pair, la fonction \(\sqrt[n]{x}\) a une racine \(x=0\) et son ordonnée à l'origine est \(y=0\). Elle est toujours positive et nulle en \(0\). Elle n'est ni paire, ni impaire. Elle est strictement croissante sur \(\mathbb{R}^+\) et a un minimum en \(x=0\). Pour \(n\) impair, la fonction \(\sqrt[n]{x}\) a une racine \(x=0\) et son ordonnée à l'origine est \(y=0\). Elle est positive pour les valeurs de \(x\) positives et négative pour les valeurs de \(x\) négatives. Elle est impaire et strictement croissante sur \(\mathbb{R}\). Elle n'a ni minimum, ni maximum.
Cliquez sur le lien pour un rappel concernant les propriétés des racines.
(e) Fonctions polynomiales
Une fonction polynomiale est une fonction du type
\(P(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_2x^2+a_1x+a_0\)
où \(n\) est un entier positif et \(a_0, a_1, a_2,\ldots,a_n\) sont des constantes, appelées les coefficients du polynôme. Le domaine de définition de n'importe quel polynôme est \(\mathbb{R}\). L'indice \(n\) du premier coefficient \(a_n\) non nul donne le degré du polynôme.
Cliquez sur le lien pour plus de détails concernant les polynômes.
- \(n=1\). Une fonction polynomiale de degré 1 est de la forme \(P(x)=ax+b\) et est appelée une fonction affine. Son graphique est la droite \(y=ax+b\) de pente \(a\) et d'ordonnée à l'origine \(b\).
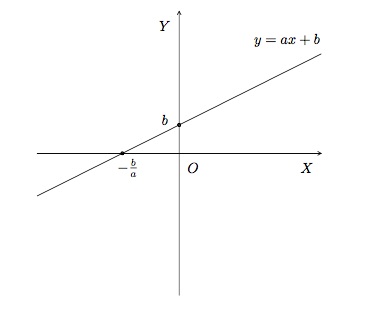
Elle possède une racine \(x=-\frac{b}{a}\) et son ordonnée à l'origine est \(y=b\). Elle est strictement croissante si \(a>0\) et strictement décroissante si \(a<0\).
Cliquez sur le lien pour un rappel sur les droites.
- Une fonction polynomiale de degré 2 est de la forme \(P(x)=ax^2+bx+c\) et est appelée une fonction quadratique. La courbe représentative de \(P\) est une parabole obtenue par déplacement de la parabole \(y=ax^2\). Voici la preuve de cette affirmation.
Cliquez sur le lien pour un rappel sur les paraboles.
(f) Fonctions rationnelles
Une fonction rationnelle \(f\) est un rapport de deux polynômes
\(f(x)=\dfrac{P(x)}{Q(x)}\)
où \(P\) et \(Q\) sont des polynômes. Le domaine de définition comprend toutes les valeurs de \(x\) qui n'annulent pas \(Q(x)\).
Par exemple, la fonction
\(f(x)=\dfrac{2x^4-x^2+1}{x^2-4}\)
est une fonction rationnelle dont le domaine de définition est \(\{x\ |\ x\neq\pm 2\}=\mathbb{R}\setminus\{-2,\, 2\}\).
(g) Fonctions trigonométriques
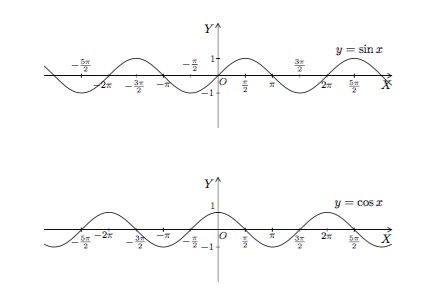
Tant pour la fonction sinus que pour la fonction cosinus, le domaine de définition est \(\mathbb{R}\) et l'ensemble image est l'intervalle fermé \([-1,1]\). En effet, quel que soit \(x\), on a
\(-1\le \sin x\le 1\mbox{ et } -1\le \cos x\le 1.\)
De plus, la fonction sinus s'annule pour chaque valeur de \(x\) égale à un multiple entier de \(\pi\). Autrement dit
\(\sin x=0 \quad\mbox{ quand }\quad x=k\pi \mbox{ avec } k \mbox{ entier}.\)
Une importante propriété des fonctions sinus et cosinus est leur caractère périodique, de période \(2\pi\). Cela signifie que, quel que soit \(x\),
\(\sin (x+2\pi)=\sin x\mbox{ et }\cos (x+2\pi)=\cos x.\)
Le caractère périodique de ces fonctions les rend particulièrement aptes à modéliser des phénomènes répétitifs comme les marées, les ressorts animés de vibrations ou les ondes sonores.
La fonction tangente est liée aux fonctions sinus et cosinus par l'équation
\(tg\, x=\dfrac{\sin x}{\cos x}.\)
Elle n'est pas définie lorsque \(\cos x=0\), c'est-à-dire lorsque \(x=\pm\pi/2, \pm 3\pi/2,\ldots\). Son ensemble image est \(\mathbb{R}\). Il est à noter que la fonction tangente est aussi périodique, mais de période \(\pi\) :
\(tg(x+\pi)=tg\, x.\)
Cliquez sur le lien pour des rappels concernant la trigonométrie.
