Théorie du module : Fonctions
Table des matières
- Définitions
- Représentation graphique
- Propriétés
- Fonctions élémentaires
- Opérations sur les fonctions
- Exemples détaillés
Propriétés
(a) Fonctions croissantes/décroissantes
On dit que la fonction est strictement croissante sur l'intervalle \([a,b]\) si la courbe représentant la fonction monte sur cet intervalle; elle est strictement décroissante sur l'intervalle \([a,b]\) si la courbe descend sur cet intervalle.
Définitions - Une fonction \(f\) est dite strictement croissante sur un intervalle \(I\) si pour tout \(x_1\), \(x_2\in I\), on a
\(x_1<x_2\Rightarrow f(x_1)<f(x_2).\)
Une fonction \(f\) est dite strictement décroissante sur un intervalle \(I\) si pour tout \(x_1\), \(x_2\in I\), on a
\(x_1<x_2\Rightarrow f(x_1)>f(x_2).\)
Une fonction \(f\) est dite monotone sur un intervalle \(I\) si elle est soit croissante, soit décroissante sur \(I\).
L'élément important dans cette définition est que l'inégalité \(f(x_1)<f(x_2)\) doit être satisfaite pour toute paire de points \(x_1\) et \(x_2\) de \(I\) qui sont tels que \(x_1<x_2\).
La fonction \(f(x)= 2x+1\) est une fonction strictement croissante. En effet, si \(x_1\), \(x_2\in\mathbb{R}\) avec \(x_1<x_2\), on a \(2x_1<2x_2\) et \(2x_1+1<2x_2+1\). Donc \(f(x_1)<f(x_2)\).
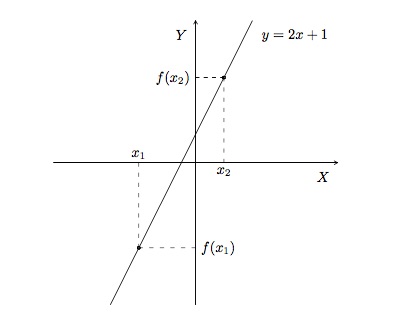
La fonction \(f(x)= -x\) est une fonction strictement décroissante. En effet, si \(x_1\), \(x_2\in\mathbb{R}\) avec \(x_1<x_2\), on a \(-x_1>-x_2\), donc \(f(x_1)>f(x_2)\).
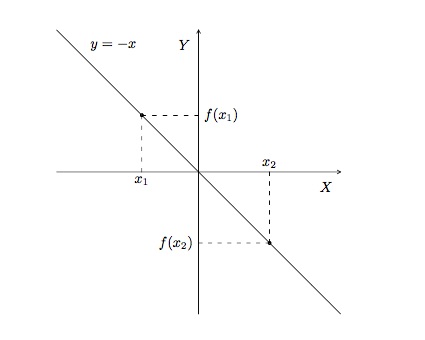
La fonction \(f(x)=\sin{x}\) n'est ni croissante, ni décroissante sur \([-2\pi,2\pi]\). En effet, on remarque sur le graphe que la courbe monte sur certains intervalles et descend sur d'autres.
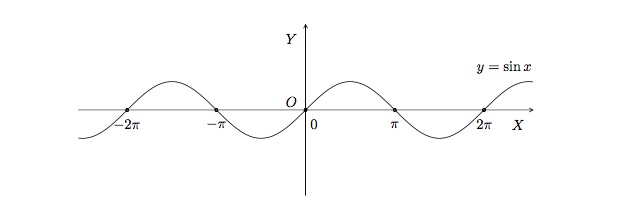
(b) Fonctions paires/impaires
Définitions - Soit \(f\), une fonction définie sur un intervalle \(I\).
La fonction \(f\) est paire si pour tout \(x\in I\), on a
\(-x\in I\mbox{ et }f(-x)=f(x).\)
La fonction \(f\) est impaire si pour tout \(x\in I\), on a
\(-x\in I\mbox{ et }f(-x)=-f(x).\)
La fonction \(f(x)=x^2\) est une fonction paire car elle est définie sur \(\mathbb{R}\) tout entier et pour tout \(x\), on a \(f(-x)=(-x)^2=x^2=f(x).\)
La fonction \(f(x)=x^3\) est impaire car elle est définie sur \(\mathbb{R}\) tout entier et pour tout \(x\), on a \(f(-x)=(-x)^3=-x^3=-f(x).\)
Graphiquement, on reconnaît une fonction paire par une symétrie de son graphique par rapport à l'axe \(OY\). En effet, les ordonnées de 2 points du graphe d'abscisses opposées sont égales. Ce qui signifie qu'ayant déjà dessiné le graphique de \(f\) pour \(x\ge 0\), nous l'obtenons tout entier en lui ajoutant simplement l'image symétrique par rapport à l'axe \(OY\).
Le graphique d'une fonction impaire est symétrique par rapport à l'origine. En effet, les ordonnées de 2 points du graphe d'abscisses opposées sont également opposés. Si nous avons déjà dessiné le graphique de \(f\) pour \(x\ge 0\), nous l'obtenons tout entier en lui adjoignant simplement l'image obtenue après une rotation de \(180^\circ\) autour de l'origine.
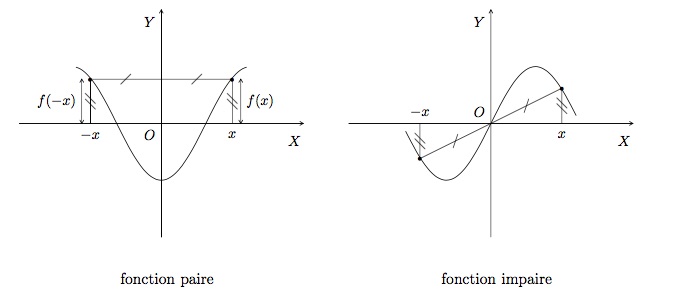
La fonction \(f(x)=x^5+x\) est impaire. En effet, pour tout \(x\in\mathbb{R}\), on a \(-x\in\mathbb{R}\) et
\(\begin{array}{lll} f(-x)&=&(-x)^5+(-x)=(-1)^5x^5+(-x)\\ &=&-x^5-x=-(x^5+x)\\ &=&-f(x). \end{array}\)
(c) Fonctions périodiques
La fonction \(f\) est périodique de période \(p\) si pour tout \(x\in D\), on a
\(f(x+p)=f(x).\)
La fonction \(f(x)=\sin{x}\) est périodique de période \(2\pi\). La fonction \(f(x)=\tan{x}\) est périodique de période \(\pi\).
