Théorie du module : Paraboles
Théorie Paraboles
Une équation du second degré à deux inconnues \(y=ax^2+bx+c\) (\(a\neq 0\)) est représentée dans le plan cartésien par une parabole. Un point appartient à cette parabole si et seulement si ses coordonnées vérifient l'équation de la parabole.
Par exemple, considérons la parabole \(P:y=2x^2+x-1\). On a \((2,9) \in P\) car \(9=2\cdot 2^2+2-1\) mais \((3,1) \not \in P\) puisque \(1\neq 2\cdot 3^2+3-1\).
En pratique, pour représenter une parabole, il faut rechercher
- le signe de \(a\) qui détermine si la parabole a un maximum (\(a < 0 \)) ou un minimum (\(a>0\));
- l'axe de symétrie de la parabole qui est une droite ayant pour équation
\(x=\frac{-b}{2a};\)
- le sommet de la parabole qui a pour coordonnées
\(S=\left(\frac{-b}{2a},\frac{-(b^2-4ac)}{4a}\right);\)
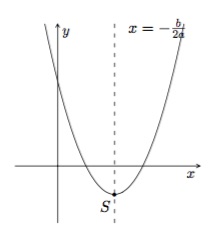
Remarque : On obtient l'ordonnée du sommet en remplaçant \(x\) par \(-\frac{b}{2a}\) dans l'équation de la parabole.
- les intersections avec l'axe \(OX\). Elles s'obtiennent en résolvant l'équation \(ax^2+bx+c=0\).
- Si \(b^2-4ac>0\), la parabole a 2 intersections avec \(OX\) :
les points \(x_1=(\frac{-b-\sqrt{b^2-4ac}}{2a},0)\) et \(x_2=(\frac{-b+\sqrt{b^2-4ac}}{2a},0)\).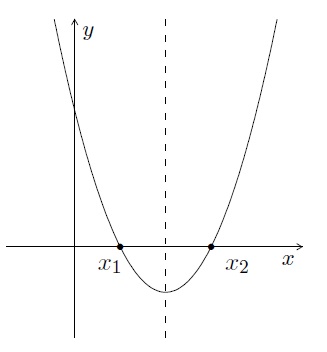
- Si \(b^2-4ac=0\), elle a une intersection avec l'axe \(OX\) : le point \(x_1=(-\frac{b}{2a},0)\).
Dans ce cas, la parabole est tangente à l'axe \(OX\) au point \(x_1\).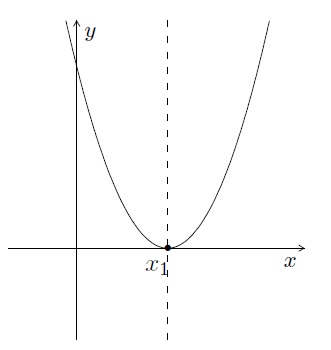
- Si \(b^2-4ac<0\), elle n'a pas d'intersection avec l'axe \(OX\).
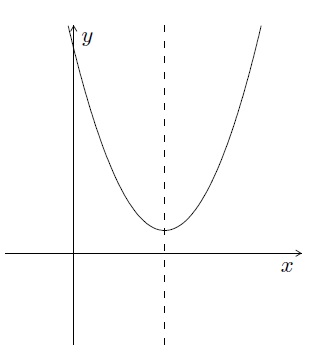
- Si \(b^2-4ac>0\), la parabole a 2 intersections avec \(OX\) :
- l'intersection avec l'axe \(OY\) qui est le point de coordonnées \((0,c)\).
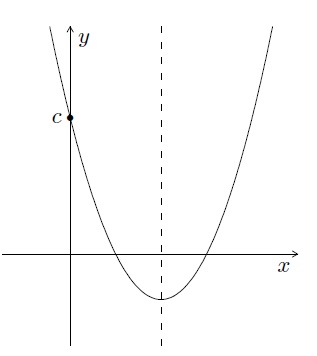
Remarque : On obtient l'intersection de la parabole avec l'axe \(OY\) en remplaçant \(x\) par \(0\) dans l'équation de la parabole.
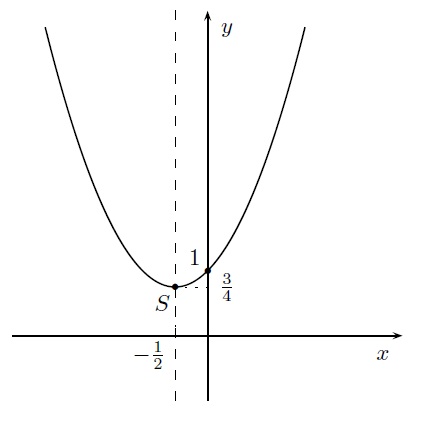
Par exemple, la parabole d'équation \(y=x^2+x+1\) possède un minimum. Son axe de symétrie est la droite \(x=-\frac{1}{2}\) et son sommet est \(S=(-\frac{1}{2},\frac{3}{4})\). Elle n'a pas d'intersection avec l'axe \(OX\) et son intersection avec l'axe \(OY\) est \((0,1)\).