Théorie du module : Nombres complexes

Table des matières

Afficher toute la théorie du module

Exemples détaillés

Calculez $(i-3)(i-2)(i-1)$.

Solution détaillée : On a

$(i-3)(i-2)(i-1)=(i^2-2i-3i+6)(i-1)=(-5i+5)(i-1)=-5i^2+5i+5i-5=10i$.

Calculez $(\sqrt[]{3}+i)^2$.

Solution détaillée : On a

$(\sqrt[]{3}+i)^2=3+2\sqrt{3}i+i^2=3+2\sqrt{3}i-1=2+2\sqrt{3}i$.

Calculez $\dfrac{4-i}{2-i}+\dfrac{4+i}{2+i}$.

Solution détaillée : On a

$\begin{array}{rcl} \dfrac{4-i}{2-i}+\dfrac{4+i}{2+i}&=&\dfrac{(4-i)(2+i)+(4+i)(2-i)}{(2-i)(2+i)}\\ &=&\dfrac{8+4i-2i-i^2+8+2i-4i-i^2}{4-i^2}\\ &=&\dfrac{16-2i^2}{5}=\dfrac{18}{5} \end{array}$

Calculez $\dfrac{\sqrt[]{3}+i}{\sqrt[]{3}-i}$.

Solution détaillée : On multiplie haut et bas par le binôme conjugué du dénominateur

$\dfrac{\sqrt[]{3}+i}{\sqrt[]{3}-i}=\dfrac{(\sqrt[]{3}+i)^2}{(\sqrt[]{3}-i)(\sqrt[]{3}+i)}=\dfrac{3+2\sqrt{3}i+i^2}{3-i^2}=\dfrac{2+2\sqrt{3}i}{4}=\dfrac{1+\sqrt{3}i}{2}$.

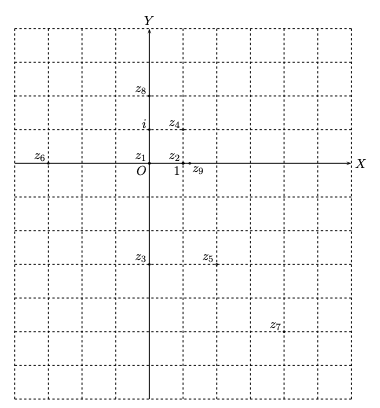
Représentez dans le plan de Gauss les nombres complexes suivants : $z_1=0,\, z_2=1,\, z_3=-3i,\, z_4=1+i,\, z_5=2-3i,\, z_6=-3,\, z_7=(3-2i)+(1-3i),\, \\ z_8=(1+i)-(1-i),\, z_9=\dfrac{2i-1}{2i+1}+\dfrac{2i+1}{2i-1},\, z_{10}=(i+1)(i+2)-(i+3)(i+4).$

Solution détaillée : On a $z_1=(0,0),\, z_2=(1,0),\, z_3=(0,-3),\, z_4=(1,1),\, z_5=(2,-3),\, z_6=(-3,0),\, \\ z_7=(3-2i)+(1-3i)=4-5i=(4,-5),\, z_8=(1+i)-(1-i)=0+2i=(0,2),\, \\ z_9=\dfrac{2i-1}{2i+1}+\dfrac{2i+1}{2i-1}=\dfrac{(2i-1)^2+(2i+1)^2}{(2i+1)(2i-1)}=\dfrac{-6}{-5}=(\frac{6}{5},0),\, \\ z_{10}=(i+1)(i+2)-(i+3)(i+4)=(3i+1)-(7i+11)=-4i-10=(-10,-4).$

Calculez les racines carrées du nombre complexe $\dfrac{1}{2}+\dfrac{\sqrt[]{3}}{2}i$.

Solution détaillée : On résoud l'équation $z^2=\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i$ où $z=x+yi$ (avec $x$ et $y\in\mathbb{R}$) et on utilise la propriété $|z^2|=|z|^2$:

$\left\{\begin{array}{l} x^2-y^2=\dfrac{1}{2}\\ 2xy=\dfrac{\sqrt{3}}{2}\\ x^2+y^2=\sqrt{\dfrac{1}{4}+\dfrac{3}{4}} \end{array}\right. \quad\iff\left\{\begin{array}{l} x^2-y^2=\dfrac{1}{2}\\ x^2+y^2=1\\ xy=\dfrac{\sqrt{3}}{4} \end{array}\right. \quad\iff\left\{\begin{array}{l} 2x^2=\dfrac{3}{2}\\ 2y^2=\dfrac{1}{2}\\ xy=\dfrac{\sqrt{3}}{4} \end{array}\right.\\ \iff\left\{\begin{array}{l} x^2=\dfrac{3}{4}\\[2mm] y^2=\dfrac{1}{4}\\[2mm] xy=\dfrac{\sqrt{3}}{4} \end{array}\right. \quad\iff\left\{\begin{array}{l} x=\pm \dfrac{\sqrt{3}}{2}\\ y=\pm \dfrac{1}{2}\\ xy=\dfrac{\sqrt{3}}{4} \quad\textrm{(positif donc $x$ et $y$ de même signe)} \end{array}\right.$

Les solutions sont $\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i$ et $-\dfrac{\sqrt{3}}{2}-\dfrac{1}{2}i$.

Résolvez l'équation $x^2+x+1=0$.

Solution détaillée : On calcule $\Delta=1-4\cdot 1\cdot 1=-3$ et donc $\sqrt[]{\Delta}=\pm\sqrt{3}i$. On obtient

$x_1=\dfrac{-1+\sqrt{3}i}{2}$ et $x_2=\dfrac{-1-\sqrt{3}i}{2}$.

Résolvez l'équation $ix^2-(5i+2)x+5(i+1)=0$.

Solution détaillée : On calcule

$\Delta=(5i+2)^2-4\cdot i\cdot 5(i+1)=25i^2+4+20i-20i^2-20i=-1$

et donc $\sqrt[]{\Delta}=\pm i$.

On obtient $x_1=\dfrac{5i+2+i}{2i}=\dfrac{6i+2}{2i}=\dfrac{(3i+1)(-i)}{1} =3-i$

et $x_2=\dfrac{5i+2-i}{2i} =\dfrac{4i+2}{2i} =\dfrac{(2i+1)(-i)}{1} =2-i$.

Les deux solutions de l'équation sont donc $3-i$ et $2-i$.

Calculez la partie réelle et la partie imaginaire du nombre complexe $z_1=\dfrac{z^2+z+1}{z^4-1}$ si $z=2+3i$.

Solution détaillée : On calcule $z^2=(2+3i)^2=4+12i+9i^2=12i-5$ et $z^4=(12i-5)^2=144i^2-120i+25=-119-120i$ et on remplace dans $z_1$ :

$\begin{array}{rcl} z_1&=&\dfrac{z^2+z+1}{z^4-1}=\dfrac{(12i-5)+(2+3i)+1}{(-119-120i)-1}\\ &=&\dfrac{15i-2}{-120-120i}=\dfrac{15i-2}{-120(1+i)}\\ &=&\dfrac{(15i-2)(1-i)}{-120(1+i)(1-i)}=\dfrac{17i+13}{-240}=\dfrac{-13}{240}-\dfrac{17}{240}i \end{array}$

La partie réelle est donc $\dfrac{-13}{240}$ et la partie imaginaire est $\dfrac{-17}{240}$.

Décomposez Le polynôme $z^4+2z^3+3z^2+4z+2$ en produit de polynômes du premier degré à coefficients complexes.

Solution détaillée : $P(z)=z^4+2z^3+3z^2+4z+2$

$P(-1)=1-2+3-4+2=0$ donc $P(z)$ est divisible par $(z+1)$. En utilisant la Règle de Horner, on obtient

$\begin{array}{c|cccc|c} &1&2&3&4&2\\ -1&&-1&-1&-2&-2\\ \hline &1&1&2&2&0 \end{array}$

$P(z)=(z+1)(z^3+z^2+2z+2)$

Factorisons $z^3+z^2+2z+2$ : $P(-1)=-1+1-2+2=0$ donc $P(z)$ est divisible par $(z+1)$

$\begin{array}{c|ccc|c} &1&1&2&2\\ -1&&-1&0&-2\\ \hline &1&0&2&0 \end{array}$

$P(z)=(z+1)^2(z^2+2)=(z+1)^2(z-\sqrt{2}i)(z+\sqrt{2}i)$.

Soit le polynôme $P(x)=x^4+4x^3+8x^2+4x+7$.
1. Calculez $P(i)$.
2. Ecrivez $P(x)$ sous la forme d'un produit de deux polynômes du deuxième degré à coefficients réels.
3. Calculez les racines de l'équation $P(x)=0$.

Solution détaillée :

On remplace $x$ par $i$ dans le polynôme : $P(i)=i^4+4i^3+8i^2+4i+7=1+4(-i)+8(-1)+4i+7=1-4i-8+4i+7=0$
Comme $P(i)=0$, $P(x)$ est divisible par $(x-i)$ et comme $P(-i)=0$, $P(x)$ est divisible par $(x+i)$. On en déduit que $P(x)$ est divisible par $(x-i)(x+i)$, c'est-à-dire par $x^2+1$.

En effectuant la division euclidienne de $x^4+4x^3+8x^2+4x+7$ par $x^2+1$ on obtient $x^2+4x+7$ et donc $P(x)=(x^2+1)(x^2+4x+7)$.

$P(x)=0 \iff (x^2+1)(x^2+4x+7)=0$

$\begin{array}{c} x^2+1=0\\ x^2=-1\\ x=\pm i \end{array}\hspace{1cm} \begin{array}{c} x^2+4x+7=0\\ \Delta = -12 \\ x=\dfrac{-4\pm 2\sqrt{3}i}{2}=-2\pm \sqrt{3}i \end{array}$

Les solutions sont donc $-i,i,-2-\sqrt{3}i \mbox{ et }-2+\sqrt{3}i $.

Ecrivez le nombre complexe $z=1+\sqrt{3}i$ sous forme trigonométrique.

Solution détaillée : On calcule le module $|z|=\sqrt{a^2+b^2}$ et l'argument $\phi$ tel que $\cos \phi =\dfrac{a}{|z|}$ et $\sin \phi =\dfrac{b}{|z|}$ :

$|z|=\sqrt[]{1+3}=2$

$\cos\phi=\dfrac{1}{2}\qquad\sin\phi=\dfrac{\sqrt{3}}{2}\qquad\Rightarrow \phi=\dfrac{\pi}{3}+2k\pi\qquad (k\in\mathbb{Z})$

Une forme trigonométrique de $z$ est donc $2(\cos \frac{\pi}{3} +i\sin \frac{\pi}{3})$.

Calculez le module et l'argument principal du nombre complexe $z=\dfrac{1-\sqrt[]{3}i}{2i}$.

Solution détaillée : On calcule le module et l'argument du numérateur et du dénominateur séparément puis on applique les règles de calcul : $|z|=\dfrac{r_1}{r_2}$ et $\phi=\phi_1-\phi_2$.

Soit $z_1=1-\sqrt{3}i$ : $r_1=2$; $\cos\phi_1=\dfrac{1}{2}$ et $\sin\phi_1=-\dfrac{\sqrt{3}}{2}$ donc $\phi_1=-\dfrac{\pi}{3}$.

Soit $z_2=2i$ : $r_2=2$; $\cos\phi_2=0$ et $\sin\phi_2=1$ donc $\phi_2=\dfrac{\pi}{2}$.

On en déduit $|z|=\dfrac{r_1}{r_2}=1$ et $\phi=\phi_1-\phi_2=-\dfrac{\pi}{3}-\dfrac{\pi}{2}=\dfrac{-5\pi}{6}$.

Calculez le module et l'argument principal du nombre complexe $z=(1-i)^2(\sqrt[]{3}-i)^3$.

Solution détaillée : On calcule le module et l'argument des différents facteurs et on applique les règles de calcul des opérations sur les nombres complexes sous forme trigonométrique.

On a $z_1=1-i$ donc $r_1=\sqrt{2}$ , $z_2=\sqrt{3}-i$ donc $r_2=2$ .

On obtient $|z|=r_1^2\cdot r_2^3=2\cdot 8=16$.

On a $z_1=1-i$ : $\cos\phi_1=\dfrac{\sqrt{2}}{2}$ , $\sin\phi_1=-\dfrac{\sqrt{2}}{2}$ donc $\phi_1=-\dfrac{\pi}{4}$.

$z_2=\sqrt{3}-i$ : $\cos\phi_2=\dfrac{\sqrt{3}}{2}$, $\sin\phi_2=\dfrac{-1}{2}$ donc $\phi_2=\dfrac{-\pi}{6}$.

On obtient $\phi=2\phi_1+3\phi_2=2(\frac{-\pi}{4})+3(\frac{-\pi}{6})=-\pi\mbox{ ou }\pi$.

Calculez le module et l'argument principal du nombre complexe $z=\dfrac{(\sqrt[]{3}-i)^3(1-i)^4}{i^7(1+i)^6}$.

Solution détaillée : On calcule le module et l'argument des différents facteurs et on applique les règles de calcul des opérations sur les nombres complexes sous forme trigonométrique.

On a $z_1=\sqrt{3}-i$ donc $r_1=2$ , $z_2=1-i$ donc $r_2=\sqrt{2}$ , $z_3=i$ donc $r_3=1$ et $z_4=1+i$ donc $r_4=\sqrt{2}$ .

On obtient $|z|=\dfrac{r_1^3\cdot r_2^4}{r_3^7\cdot r_4^6}=\dfrac{2^3\cdot (\sqrt{2})^4}{1^7\cdot (\sqrt{2})^6}=4$.

On a $z_1=\sqrt{3}-i$ : $\cos\phi_1=\dfrac{\sqrt{3}}{2}$ , $\sin\phi_1=-\dfrac{1}{2}$ donc $\phi_1=-\dfrac{\pi}{6}$.

$z_2=1-i$ : $\cos\phi_2=\dfrac{\sqrt{2}}{2}$, $\sin\phi_2=-\dfrac{\sqrt{2}}{2}$ donc $\phi_2=\dfrac{-\pi}{4}$.

$z_3=i$ : $\cos\phi_3=0$, $\sin\phi_3=1$ donc $\phi_3=\dfrac{\pi}{2}$.

$z_4=1+i$ : $\cos\phi_4=\dfrac{\sqrt{2}}{2}$, $\sin\phi_4=\dfrac{\sqrt{2}}{2}$ donc $\phi_4=\dfrac{\pi}{4}$.

On obtient

$\begin{array}{rcl} \phi&=&(3\phi_1+4\phi_2)-(7\phi_3+6\phi_4)\\ &=&(3(-\frac{\pi}{6})+4(\frac{-\pi}{4}))-(7(\frac{\pi}{2})+6(\frac{\pi}{4}))\\ &=&\dfrac{-13\pi}{2}=\dfrac{-\pi}{2} \end{array}$.

Résolvez l'équation $z^3=8i$.

Solution détaillée : On va mettre le nombre $8i$ sous forme trigonométrique $8i=r_1(\cos\phi_1+i\sin\phi_1)$ en recherchant $r_1$ et $\phi_1$ puis on résoud l'équation $z^3=r_1(\cos\phi_1+i\sin\phi_1)$ où $z=r(\cos\phi+i\sin\phi)$.

$8i=r_1(\cos\phi_1+i\sin\phi_1)$ donc $r_1=8$ et $\cos\phi_1+i\sin\phi_1=i$ donc $\phi_1=\dfrac{\pi}{2}$.

Résolvons l'équation $z^3=8(\cos\frac{\pi}{2}+i\frac{\pi}{2})$ où $z=r(\cos\phi+i\sin\phi)$.

On a donc $r^3(\cos3\phi+i\sin3\phi)=8(\cos\frac{\pi}{2}+i\frac{\pi}{2})$

Et par suite,

$\left\{\begin{array}{rl} r^3&=8\\ 3\phi&=\dfrac{\pi}{2}+2k\pi\quad(k\in\mathbb{Z}) \end{array} \right.\qquad \left\{\begin{array}{rl} r&=2\\ \phi&=\dfrac{\dfrac{\pi}{2}+2k\pi}{3}\quad(k\in\mathbb{Z}) \end{array} \right.$

En donnant des valeurs $\{0,1,2\}$ à $k$, il vient

$z_0=2\;(\cos\,\,\frac{\pi}{6}+i\sin\,\,\frac{\pi}{6})=\sqrt[]{3}+i$

$z_1=2\;(\cos\,\frac{5\pi}{6}+i\sin\,\frac{5\pi}{6})=-\sqrt[]{3}+i$

$z_2=2\;(\cos\,\frac{9\pi}{6}+i\sin\frac{9\pi}{6})=-2i$

Résolvez l'équation $z^5=2-2i$.

Solution détaillée : On va mettre le nombre $2-2i$ sous forme trigonométrique $2-2i=r_1(\cos\phi_1+i\sin\phi_1)$ en recherchant $r_1$ et $\phi_1$ puis on résoud l'équation $z^5=r_1(\cos\phi_1+i\sin\phi_1)$ où $z=r(\cos\phi+i\sin\phi)$.

$2-2i=r_1(\cos\phi_1+i\sin\phi_1)$, $r_1=2\sqrt{2}$, $\cos\phi_1=\dfrac{\sqrt{2}}{2}$ et $\sin\phi_1=\dfrac{-\sqrt{2}}{2}$ donc $\phi_1=\dfrac{-\pi}{4}$.

Résolvons l'équation $z^5=2\sqrt{2}(\cos\frac{-\pi}{4}+i\sin\frac{-\pi}{4})$ où $z=r(\cos\phi+i\sin\phi)$.

On a $r^5(\cos5\phi+i\sin5\phi)=2\sqrt{2}(\cos\frac{-\pi}{4}+i\sin\frac{-\pi}{4})$

et par suite,

$\left\{\begin{array}{rl} r^5&=2\sqrt{2}\\ 5\phi&=\dfrac{-\pi}{4}+2k\pi\quad(k\in\mathbb{Z}) \end{array} \right. \qquad \left\{\begin{array}{rl} r&=\sqrt[5]{2\sqrt{2}}=\sqrt[10]{8}\\ \phi&=\dfrac{\dfrac{-\pi}{4}+2k\pi}{5}\qquad(k\in\mathbb{Z}) \end{array} \right.$

En donnant des valeurs $\{0,1,2,3,4\}$ à $k$, il vient

$z_0=\sqrt[10]{8}\;(\cos\,\,\frac{-\pi}{20}+i\sin\,\,\frac{-\pi}{20})$

$z_1=\sqrt[10]{8}\;(\cos\,\frac{7\pi}{20}+i\sin\,\frac{7\pi}{20})$

$z_2=\sqrt[10]{8}\;(\cos\,\frac{3\pi}{4}+i\sin\frac{3\pi}{4})$

$z_3=\sqrt[10]{8}\;(\cos\,\frac{23\pi}{20}+i\sin\,\frac{23\pi}{20})$

$z_4=\sqrt[10]{8}\;(\cos\,\frac{31\pi}{20}+i\sin\,\frac{31\pi}{20})$

qui sont les cinq racines cinquièmes de $2-2i$.

Théorie

Retour au module