Théorie du module : Nombres complexes
Table des matières
- L'ensemble des nombres complexes
- Equations du deuxième degré
- Forme trigonométrique d'un nombre complexe
- Exponentielle complexe
- Exemples détaillés
Forme trigonométrique d'un nombre complexe
Soit le nombre complexe \(z=a+bi\) représenté dans le plan cartésien par le point \(P=(a,b)\).
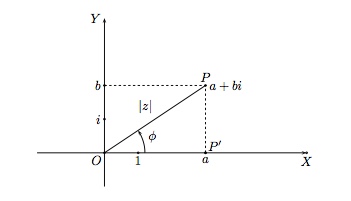
Remarque : Il existe une infinité d'arguments d'un nombre complexe non nul qui diffèrent d'un multiple entier de \(2\pi\). On dit alors que l'argument d'un complexe est défini modulo \(2\pi\). On le note \(\phi+2k\pi,\, k\in\mathbb{Z}.\) L'argument principal est l'unique mesure de \(\phi\) qui est comprise entre \(-\pi\) et \(\pi\).
(a) Calcul du module et de l'argument d'un nombre complexe
Dans le triangle rectangle \(OP'P\) on a d'une part \(|z|^2=a^2+b^2\) et donc
\(|z|=\sqrt[]{a^2+b^2}\)
et d'autre part,
\(\cos\phi=\dfrac{a}{|z|}\qquad \textrm{et}\qquad \sin\phi=\dfrac{b}{|z|}.\)
Le nombre complexe \(z=a+bi\) peut donc s'écrire
\(z=|z|\cos\phi+|z|\sin\phi\;i=|z|(\cos\phi+i\sin\phi).\)
Par exemple cherchons la forme trigonométrique du nombre complexe \(z=\sqrt[]{3}-i\). On calcule
\(|z|=\sqrt{3+1}=2\)
et
\(\cos\phi=\dfrac{\sqrt[]{3}}{2},\qquad\sin\phi=\dfrac{-1}{2}\qquad\Rightarrow \phi=\dfrac{11\pi}{6}.\)
Le nombre complexe \(z=\sqrt[]{3}-i\) peut donc aussi s'écrire \(z=2\left(\cos(\frac{11\pi}{6})+i\sin(\frac{11\pi}{6})\right).\)
Le nombre complexe \(z=i\) peut encore s'écrire \(z=\cos(\frac{\pi}{2})+i\sin(\frac{\pi}{2}).\) En effet, on calcule
\(|z|=\sqrt{0+1}=1\)
et
\(\cos\phi=\dfrac{0}{1}=0,\qquad\sin\phi=\dfrac{1}{1}=1\qquad\Rightarrow \phi=\dfrac{\pi}{2}.\)
Remarque : Deux nombres complexes conjugués ont le même module et des arguments opposés :
\(z=a+bi=|z|(\cos\phi+i\sin\phi)\qquad\textrm{ et}\qquad \bar{z}=a-bi=|z|(\cos(-\phi)+i\sin(-\phi)).\)
(b) Produit de deux nombres complexes
Soient les nombres complexes \(z_1=|z_1|(\cos \phi_1+i\sin \phi_1)\) et \(z_2=|z_2|(\cos \phi_2+i\sin \phi_2)\). Le produit de deux nombres complexes non nuls a pour module le produit des modules de ces deux nombres complexes et pour argument la somme des arguments de ces nombres complexes :
\(z_1\cdot z_2=|z_1|\, |z_2|\;(\cos (\phi_1+\phi_2)+i\sin (\phi_1+\phi_2)).\)
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation
Par exemple, pour \(z_1=3\;(\cos(\frac{\pi}{9})+i\sin(\frac{\pi}{9}))\) et \(z_2=\sqrt[]{3}\;(\cos(\frac{7\pi}{18})+i\sin(\frac{7\pi}{18}))\) on a
\(z_1\cdot z_2=3\,\sqrt[]{3}\;(\cos (\frac{\pi}{9}+\frac{7\pi}{18})+i\sin (\frac{\pi}{9}+\frac{7\pi}{18})) =3\,\sqrt[]{3}\;(\cos(\frac{\pi}{2})+i\sin(\frac{\pi}{2})) =3\,\sqrt[]{3}i.\)
(c) Quotient de deux nombres complexes
Soient les nombres complexes \(z_1=|z_1|(\cos \phi_1+i\sin \phi_1)\) et \(z_2=|z_2|(\cos \phi_2+i\sin \phi_2)\). Le quotient de deux nombres complexes non nuls a pour module le quotient des modules de ces deux nombres et pour argument la différence des arguments de ces deux nombres :
\(\dfrac{z_1}{z_2}= \dfrac{|z_1|}{|z_2|}(\cos(\phi_1-\phi_2)+i\sin(\phi_1-\phi_2)).\)
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation
Par exemple, pour \(z_1=\cos(\frac{3\pi}{2})+i\sin(\frac{3\pi}{2})\) et \(z_2=2\;(\cos(\frac{\pi}{3})+i\sin(\frac{\pi}{3}))\) on a
\(\dfrac{z_1}{z_2}=\dfrac{1}{2}\;\left(\cos(\frac{3\pi}{2}-\frac{\pi}{3}))+i\sin(\frac{3\pi}{2}-\frac{\pi}{3})\right) =\dfrac{1}{2}\left(\cos(\frac{7\pi}{6})+i\sin(\frac{7\pi}{6})\right) =\dfrac{-\,\sqrt[]{3}}{4}-\dfrac{1}{4}i.\)
Inverse d'un nombre complexe
En particulier, si \(z_1=1\), nous avons
\(\dfrac{1}{z_2}=\dfrac{1}{|z_2|}\;(\cos(-\phi_2)+i(-\phi_2)).\)
L'inverse d'un nombre complexe non nul a pour module l'inverse du module de ce nombre et pour argument, l'opposé de l'argument de ce nombre.
(d) Puissance d'un nombre complexe
Soit \(z=|z|\;(\cos\,\phi+i\sin\,\phi)\) un nombre complexe et \(n\) un nombre naturel. En appliquant la règle du produit, nous obtenons
\(z^n=|z|^n\;(\cos(n\phi)+i\sin(n\phi)).\)
Par exemple, calculons \((-1+i)^4\). On a
\(-1+i=\sqrt[]{2}\;(\cos(\frac{3\pi}{4})+i\sin(\frac{3\pi}{4}))\)
et donc
\((-1+i)^4 =4\;(\cos(\frac{12\pi}{4})+i\sin(\frac{12\pi}{4})) =4\;(\cos\pi+i\sin\pi) =-4.\)
Proposition (Formule de Moivre) - Pour tout nombre naturel \(n\) on a
\((\cos\,\phi+i\sin\,\phi)^n=(\cos(n\phi)+i\sin(n\phi)).\)
Il s'agit du cas particulier où \(|z|=1\). En effet, dans ce cas, on a
\(z^n=(\cos(\phi)+i\sin(\phi))^n=\cos(n\phi)+i\sin(n\phi).\)
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation
Remarque : La formule de Moivre reste valable pour des puissances dont l'exposant est un nombres entier strictement négatif. En effet, on a
\((\cos\,\phi+i\sin\,\phi)^{-n}=\dfrac{1}{(\cos\,\phi+i\sin\,\phi)^n} =\dfrac{1}{\;(\cos(n\phi)+i\sin(n\phi))} =\;(\cos\,(-n\phi)+i\sin\,(-n\phi)).\)
(e) Racines nièmesd'un nombre complexe
Calculer les racines nièmes d'un nombre complexe \(r_1\;(\cos\,\phi_1+i\sin\,\phi_1)\) revient à chercher \(z\) tel que \(z^n=r_1\;(\cos\,\phi_1+i\sin\,\phi_1).\) On obtient \(n\) racines nièmes distinctes :
\(z_k=\sqrt[n]{r_1}\left(\cos(\frac{\phi_1+2k\pi}{n})+i\sin(\frac{\phi_1+2k\pi}{n})\right),\qquad k\in \{0,1,2,\cdots n-1\}.\)
Par exemple, calculons les racines sixièmes de \(-64\). On peut écrire \(-64=64\;(\cos\,\pi+i\sin\,\pi)\) et il reste à résoudre l'équation \(z^6=64\;(\cos\,\pi+i\sin\,\pi).\) Pour cela, posons \(z=r\;(\cos\,\phi+i\sin\,\phi)\), on a donc
\(r^6\;(\cos(6\phi)+i\sin(6\phi))=64\;(\cos\,\pi+i\sin\,\pi)\)
ce qui implique \(\left\{\begin{array}{rcl} r^6&=&64\\ 6\phi&=&\pi+2k\pi\quad(k\in\mathbb{Z}) \end{array} \right.\) et donc \(\left\{\begin{array}{rcl} r&=&2\\ \phi&=&\dfrac{\pi+2k\pi}{6}\quad(k\in\mathbb{Z}) \end{array} \right.\)
En donnant des valeurs \(\{0,1,2,3,4,5\}\) à \(k\), on trouve les six racines sixièmes de \(-64\) :
\(\begin{array}{ll} z_0=2\;(\cos(\frac{\pi}{6})+i\sin(\frac{\pi}{6}))=\sqrt[]{3}+i&z_3=2\;(\cos(\frac{7\pi}{6})+i\sin(\frac{7\pi}{6}))=-\sqrt[]{3}-i\\[2mm] z_1=2\;(\cos(\frac{\pi}{2})+i\sin(\frac{\pi}{2}))=2i&z_4=2\;(\cos(\frac{3\pi}{2})+i\sin(\frac{3\pi}{2}))=-2i\\[2mm] z_2=2\;(\cos(\frac{5\pi}{6})+i\sin(\frac{5\pi}{6}))=-\sqrt[]{3}+i\hspace{1cm}&z_5=2\;(\cos(\frac{11\pi}{6})+i\sin(\frac{11\pi}{6}))=\sqrt[]{3}-i \end{array}\)
Si on représente ces racines dans le plan de Gauss, on remarque qu'elles forment les sommets d'un hexagone régulier inscrit dans un cercle de centre \((0,0)\) et de rayon \(2=\sqrt[6]{64}\).
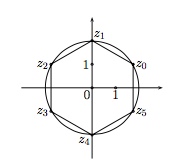
Plus généralement, les racines nièmes du nombre complexe \(r_1\;(\cos\,\phi_1+i\sin\,\phi_1)\) dans le plan de Gauss sont les sommets d'un polygone régulier à \(n\) côtés inscrit dans le cercle de centre \((0,0)\) et de rayon \(\sqrt[n]{r_1}\).
