Théorie du module : Nombres complexes
Table des matières
- L'ensemble des nombres complexes
- Equations du deuxième degré
- Forme trigonométrique d'un nombre complexe
- Exponentielle complexe
- Exemples détaillés
L'ensemble des nombres complexes
Dans l'ensemble des nombres réels l'équation \(x^2+1=0\) n'admet pas de solution. Nous allons donc définir un ensemble de nombres tels que toute équation du deuxième degré admette au moins une solution. Cet ensemble est l'ensemble des nombres complexes. Il est noté \(\mathbb{C}\).
(a) Définitions
Si \(a=0\) et \(b\not=0\), on dit que \(z=bi\) est un imaginaire pur. Le nombre complexe \(\bar{z}=a-bi\) est le conjugué de \(z=a+bi\).
Par exemple, les nombres \(-3i,\, 2+5i,\, 4,\, 3-4i\) sont des nombres complexes et \(-3i\) est un imaginaire pur.
(b) Propriétés et règles de calcul
On suppose que \(a\) et \(b\) sont des nombres réels. On a les propriétés suivantes.
Egalité de deux nombres complexes
Deux nombres complexes sont égaux si et seulement si leurs parties réelles sont égales et leurs parties imaginaires sont égales : \(a+bi=c+di\iff a=c \quad\textrm{et}\quad b=d.\)
Addition et multiplication de deux nombres complexes
L'addition et la multiplication dans \(\mathbb{C}\) sont définies respectivement par
\( (a+bi)+(c+di)=(a+c)+(b+d)i \)
et
\( (a+bi)(c+di)=(ac-bd)+(ad+bc)i. \)
En effet, on a
\(\begin{split} (a+bi)+(c+di)&=a+bi+c+di\\ &=(a+c)+(b+d)i \end{split}\)
et
\(\begin{split} (a+bi)(c+di)&=ac+adi+bci+bdi^2\\ &=ac+(ad+bc)i-bd\\ &=(ac-bd)+(ad+bc)i. \end{split}\)
Par exemple, on a \((3+4i)+(5-3i)=8+i\) et \((3+i)(2-3i)=6-9i+2i-3i^2=6-7i+3=9-7i.\)
Eléments neutres
Le nombre \(0\) est neutre pour l'addition et le nombre \(1\) est neutre pour la multiplication.
Opposé d'un nombre complexe
L'opposé du nombre complexe \(a+bi\) est le nombre complexe \(-a-bi. \)
Inverse d'un nombre complexe
L'inverse du nombre complexe \(a+bi\) est le nombre complexe \(\dfrac{a}{a^2+b^2}-\dfrac{b}{a^2+b^2}i.\)
En effet, soit \(x+yi\) l'inverse de \(a+bi\). On a alors
\(\begin{split} &(a+bi)(x+yi)=1\\ &\iff ax-by+(ay+bx)i=1\\ &\iff \left\{\begin{array}{l} ax-by=1\\ bx+ay=0 \end{array}\right.\\ &\iff \left\{\begin{array}{l} x=\dfrac{1}{a}(1+by)\\ b\cdot\dfrac{1}{a}(1+by)+ay=0 \end{array}\right.\\ &\iff \left\{\begin{array}{l} x=\dfrac{1}{a}(1+by)\\ \dfrac{1}{a}(b+b^2y+a^2y)=0 \end{array}\right.\\ &\iff \left\{\begin{array}{l} x=\dfrac{1}{a}(1+by)\\ y=\dfrac{-b}{a^2+b^2} \end{array}\right.\\ &\iff \left\{\begin{array}{l} x=\dfrac{1}{a}(1-\dfrac{b^2}{a^2+b^2})\\ y=\dfrac{-b}{a^2+b^2} \end{array}\right.\\ &\iff \left\{\begin{array}{l} x=\dfrac{a}{a^2+b^2}\\ y=\dfrac{-b}{a^2+b^2} \end{array}\right. \end{split}\)
Produit de deux nombres complexes conjugués
Le produit de deux nombres complexes conjugués est un nombre réel positif :
\((a+bi)(a-bi)=a^2+b^2 \)
En effet, on calcule
\(\begin{split} (a+bi)(a-bi)&=a^2-abi+abi-b^2i^2\\ &=a^2+b^2 \end{split}\)
Par exemple, on a \((5+7i)(5-7i)=25-49i^2=25+49=74.\)
Quotient de deux nombres complexes
Pour diviser deux nombres complexes, on multiplie et on divise le quotient par le complexe conjugué du dénominateur.
Par exemple, on calcule
\(\dfrac{3+i}{2-3i}=\dfrac{(3+i)(2+3i)}{(2-3i)(2+3i)}=\dfrac{6+9i+2i-3}{4+9}=\dfrac{3+11i}{13}=\dfrac{3}{13}+\dfrac{11}{13}i.\)
Puissances de \(i\)
Voici les puissances de \(i\) à exposants naturels :
\(i^0=1,\, i^2=-1,\, i^3=i^2\cdot i=-i,\, i^4=i^2\cdot i^2=(-1)(-1)=1,\, i^5=i^4\cdot i=i,\, \ldots\)
(c) Représentation graphique des nombres complexes
Un nombre complexe \(z=a+bi\) peut être représenté comme un couple de nombres réels \((a,b)\) où \(a\) est la partie réelle de \(z\) et \(b\) sa partie imaginaire. On définit ainsi une bijection
\(f\, :\, \mathbb{R}^2\to \mathbb{C}\, ;\, (a,b)\mapsto a+bi\)
telle que tout couple de réels a pour image un et un seul nombre complexe.
Dans le plan muni d'un repère orthonormé, un nombre complexe \(z=a+bi\) est donc représenté par le point \(P\) de coordonnées \((a,b)\).
Le plan muni d'un repère orthonormé représentant l'ensemble des nombres complexes est appelé plan de Gauss ou plan complexe. L'axe \(OX\) est appelé l'axe réel et l'axe \(OY\) est appalé l'axe imaginaire.
La distance \(|OP|\) est le module du nombre complexe \(z=a+bi\). On le note \(|z|=|a+bi|=\sqrt{a^2+b^2}.\)
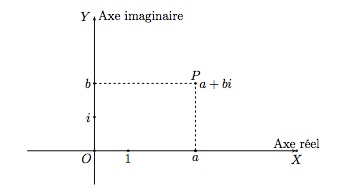
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation
(d) Racine carrée d'un nombre complexe
Pour déterminer les racines carrées de \(a+bi\), on pose \(z=x+yi\) et on résoud l'équation \(z^2=a+bi\) (où \(x\) et \(y\) sont des nombres réels) en utilisant la propriété du module \(|z^2|=|z|^2.\) On obtient
\((x+yi)^2=a+bi\iff x^2-y^2+2xyi=a+bi\)
et
\(|a+bi|=|z^2|=|(x+yi)^2|=|x+yi|^2\)
\(\sqrt{a^2+b^2}=x^2+y^2\)
Il reste à résoudre le système
\(\left\{\begin{array}{l} x^2-y^2=a\\ 2xy=b\\ x^2+y^2=\sqrt{a^2+b^2} \end{array}\right.\)
Calculons par exemple les racines carrées de \(5+12i\). Il faut résoudre le système
\(\left\{\begin{array}{l} x^2-y^2=5\\ 2xy=12\\ x^2+y^2=\sqrt{5^2+12^2} \end{array}\right.\)
On obtient
\(\left\{\begin{array}{l} x^2-y^2=5\\ 2xy=12\\ x^2+y^2=\sqrt{5^2+12^2} \end{array}\right. \qquad\iff\left\{\begin{array}{l} x^2-y^2=5\\ x^2+y^2=13\\ xy=6 \end{array}\right.\qquad\iff\left\{\begin{array}{l} 2x^2=18\\ 2y^2=8\\ xy=6 \end{array}\right.\qquad\iff \left\{\begin{array}{l} x^2=9\\ y^2=4\\ xy=6 \end{array}\right.\)
et donc \(xy\) étant positif, \(x\) et \(y\) sont de même signe. On en déduit que \(5+12i\) a deux racines carrées opposées : \(3+2i\) et \(-3-2i\).
