Théorie du module : Nombres complexes

L'ensemble des nombres complexes

Dans l'ensemble des nombres réels l'équation \(x^2+1=0\) n'admet pas de solution.  Nous allons donc définir un ensemble de nombres tels que toute équation du deuxième degré admette au moins une solution.  Cet ensemble est l'ensemble des nombres complexes. Il est noté \(\mathbb{C}\).

(a) Définitions

Par exemple, les nombres \(-3i,\, 2+5i,\, 4,\, 3-4i\) sont des nombres complexes et \(-3i\) est un imaginaire pur.

(b) Propriétés et règles de calcul

On suppose que \(a\) et \(b\) sont des nombres réels.  On a les propriétés suivantes. 

Egalité de deux nombres complexes

Deux nombres complexes sont égaux si et seulement si leurs parties réelles sont égales et leurs parties imaginaires sont égales : \(a+bi=c+di\iff a=c \quad\textrm{et}\quad b=d.\)

 

Addition et multiplication de deux nombres complexes

L'addition et la multiplication dans \(\mathbb{C}\) sont définies respectivement par

\( (a+bi)+(c+di)=(a+c)+(b+d)i \)

et

\( (a+bi)(c+di)=(ac-bd)+(ad+bc)i. \)

 

En effet, on a

\(\begin{split} (a+bi)+(c+di)&=a+bi+c+di\\ &=(a+c)+(b+d)i \end{split}\)

et

\(\begin{split} (a+bi)(c+di)&=ac+adi+bci+bdi^2\\ &=ac+(ad+bc)i-bd\\ &=(ac-bd)+(ad+bc)i. \end{split}\)

Par exemple, on a \((3+4i)+(5-3i)=8+i\) et \((3+i)(2-3i)=6-9i+2i-3i^2=6-7i+3=9-7i.\)

 

Eléments neutres

Le nombre \(0\) est neutre pour l'addition et le nombre \(1\) est neutre pour la multiplication.

 

Opposé d'un nombre complexe

L'opposé du nombre complexe \(a+bi\) est le nombre complexe \(-a-bi. \)

 

Inverse d'un nombre complexe

L'inverse du nombre complexe \(a+bi\) est le nombre complexe \(\dfrac{a}{a^2+b^2}-\dfrac{b}{a^2+b^2}i.\)

En effet, soit \(x+yi\) l'inverse de \(a+bi\).  On a alors

\(\begin{split} &(a+bi)(x+yi)=1\\ &\iff ax-by+(ay+bx)i=1\\ &\iff \left\{\begin{array}{l} ax-by=1\\ bx+ay=0 \end{array}\right.\\ &\iff \left\{\begin{array}{l} x=\dfrac{1}{a}(1+by)\\ b\cdot\dfrac{1}{a}(1+by)+ay=0 \end{array}\right.\\ &\iff \left\{\begin{array}{l} x=\dfrac{1}{a}(1+by)\\ \dfrac{1}{a}(b+b^2y+a^2y)=0 \end{array}\right.\\ &\iff \left\{\begin{array}{l} x=\dfrac{1}{a}(1+by)\\ y=\dfrac{-b}{a^2+b^2} \end{array}\right.\\ &\iff \left\{\begin{array}{l} x=\dfrac{1}{a}(1-\dfrac{b^2}{a^2+b^2})\\ y=\dfrac{-b}{a^2+b^2} \end{array}\right.\\ &\iff \left\{\begin{array}{l} x=\dfrac{a}{a^2+b^2}\\ y=\dfrac{-b}{a^2+b^2} \end{array}\right. \end{split}\)

 

Produit de deux nombres complexes conjugués

Le produit de deux nombres complexes conjugués est un nombre réel positif :

\((a+bi)(a-bi)=a^2+b^2 \)

En effet, on calcule

\(\begin{split} (a+bi)(a-bi)&=a^2-abi+abi-b^2i^2\\ &=a^2+b^2 \end{split}\)

Par exemple, on a \((5+7i)(5-7i)=25-49i^2=25+49=74.\)

 

Quotient de deux nombres complexes

Pour diviser deux nombres complexes, on multiplie et on divise le quotient par le complexe conjugué du dénominateur.

Par exemple, on calcule

\(\dfrac{3+i}{2-3i}=\dfrac{(3+i)(2+3i)}{(2-3i)(2+3i)}=\dfrac{6+9i+2i-3}{4+9}=\dfrac{3+11i}{13}=\dfrac{3}{13}+\dfrac{11}{13}i.\)

 

Puissances de \(i\)

Voici les puissances de \(i\) à exposants naturels :

\(i^0=1,\, i^2=-1,\, i^3=i^2\cdot i=-i,\, i^4=i^2\cdot i^2=(-1)(-1)=1,\, i^5=i^4\cdot i=i,\, \ldots\)

 

(c) Représentation graphique des nombres complexes

Un nombre complexe \(z=a+bi\) peut être représenté comme un couple de nombres réels \((a,b)\) où \(a\) est la partie réelle de \(z\) et \(b\) sa partie imaginaire.  On définit ainsi une bijection

\(f\, :\, \mathbb{R}^2\to \mathbb{C}\, ;\, (a,b)\mapsto a+bi\)

telle que tout couple de réels a pour image un et un seul nombre complexe.

Dans le plan muni d'un repère orthonormé, un nombre complexe \(z=a+bi\) est donc représenté par le point \(P\) de coordonnées \((a,b)\).

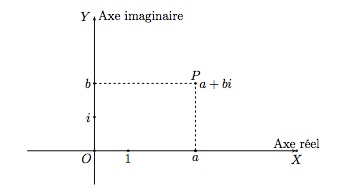
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation

(d) Racine carrée d'un nombre complexe

Pour déterminer les racines carrées de \(a+bi\), on pose \(z=x+yi\) et on résoud l'équation \(z^2=a+bi\) (où \(x\) et \(y\) sont des nombres réels) en utilisant la propriété du module \(|z^2|=|z|^2.\)  On obtient

\((x+yi)^2=a+bi\iff x^2-y^2+2xyi=a+bi\)

et

\(|a+bi|=|z^2|=|(x+yi)^2|=|x+yi|^2\)

\(\sqrt{a^2+b^2}=x^2+y^2\)

Il reste à résoudre le système

\(\left\{\begin{array}{l} x^2-y^2=a\\ 2xy=b\\ x^2+y^2=\sqrt{a^2+b^2} \end{array}\right.\)

Calculons par exemple les racines carrées de \(5+12i\).  Il faut résoudre le système

\(\left\{\begin{array}{l} x^2-y^2=5\\ 2xy=12\\ x^2+y^2=\sqrt{5^2+12^2} \end{array}\right.\)

On obtient

\(\left\{\begin{array}{l} x^2-y^2=5\\ 2xy=12\\ x^2+y^2=\sqrt{5^2+12^2} \end{array}\right. \qquad\iff\left\{\begin{array}{l} x^2-y^2=5\\ x^2+y^2=13\\ xy=6 \end{array}\right.\qquad\iff\left\{\begin{array}{l} 2x^2=18\\ 2y^2=8\\ xy=6 \end{array}\right.\qquad\iff \left\{\begin{array}{l} x^2=9\\ y^2=4\\ xy=6 \end{array}\right.\)

et donc \(xy\) étant positif, \(x\) et \(y\) sont de même signe.  On en déduit que \(5+12i\) a deux racines carrées opposées : \(3+2i\) et \(-3-2i\).

Equations du deuxième degré

Nous avons vu ici comment résoudre une équation du second degré dans \(\mathbb{R}\).  Une telle équation n'aura pas de solution si \(\Delta=b^2-4ac<0\).  Dans \(\mathbb{C}\), la racine carrée d'un nombre négatif existe.  Une équation du second degré aura donc toujours deux solutions (distinctes ou non).

Pour trouver les solutions de l'équation \(ax^2+bx+c=0\) avec \(a,\, b,\, c\in\mathbb{C}\), on calcule \(\Delta=b^2-4ac\) et on a

\(S=\left\{\dfrac{-b+\sqrt{\Delta}}{2a},\dfrac{-b-\sqrt{\Delta}}{2a}\right\}.\)

 

Par exemple, cherchons les solutions de l'équation \(x^2-x+2=0\).  On calcule \(\Delta=1-8=-7=7i^2\) et donc cette équation a deux solutions dans \(\mathbb{C}\) :

\(x_1=\dfrac{1+i\sqrt{7}}{2}=\dfrac{1}{2}+\dfrac{\sqrt{7}}{2}i\hspace{1cm}\mbox{ et }\hspace{1cm}x_2=\dfrac{1-i\sqrt{7}}{2}=\dfrac{1}{2}-\dfrac{\sqrt{7}}{2}i.\)

Cherchons les solutions de l'équation \(2ix^2-(1+2i)x+i-1=0\). On calcule

\(\Delta=(1+2i)^2-8i(i-1)=1+4i-4+8+8i=5+12i\). 

On a vu ci-dessus que le nombre complexe \(5+12i\) a deux racines opposées \(3+2i\) et \(-3-2i\).  On en déduit les deux solutions de l'équation de départ

\(x_1=\dfrac{1+2i+3+2i}{4i} =\dfrac{1+i}{i} =\dfrac{(1+i)(-i)}{i(-i)} =1-i\)

et

\(x_2=\dfrac{1+2i-3-2i}{4i} =\dfrac{-2}{4i} =\dfrac{-1}{2i} =\dfrac{i}{2}.\)

Forme trigonométrique d'un nombre complexe

Soit le nombre complexe \(z=a+bi\) représenté dans le plan cartésien par le point \(P=(a,b)\).

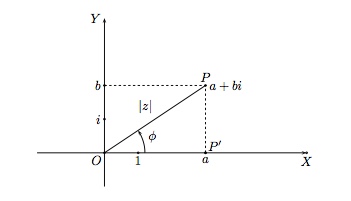
Remarque : Il existe une infinité d'arguments d'un nombre complexe non nul qui diffèrent d'un multiple entier de \(2\pi\). On dit alors que l'argument d'un complexe est défini modulo \(2\pi\).  On le note \(\phi+2k\pi,\, k\in\mathbb{Z}.\)  L'argument principal est l'unique mesure de \(\phi\) qui est comprise entre \(-\pi\) et \(\pi\).

(a) Calcul du module et de l'argument d'un nombre complexe

Dans le triangle rectangle \(OP'P\) on a d'une part \(|z|^2=a^2+b^2\) et donc

\(|z|=\sqrt[]{a^2+b^2}\)

et d'autre part,

\(\cos\phi=\dfrac{a}{|z|}\qquad \textrm{et}\qquad \sin\phi=\dfrac{b}{|z|}.\)

Le nombre complexe \(z=a+bi\) peut donc s'écrire

\(z=|z|\cos\phi+|z|\sin\phi\;i=|z|(\cos\phi+i\sin\phi).\)
 

Par exemple cherchons la forme trigonométrique du nombre complexe \(z=\sqrt[]{3}-i\).  On calcule

\(|z|=\sqrt{3+1}=2\)

et

\(\cos\phi=\dfrac{\sqrt[]{3}}{2},\qquad\sin\phi=\dfrac{-1}{2}\qquad\Rightarrow \phi=\dfrac{11\pi}{6}.\)

Le nombre complexe \(z=\sqrt[]{3}-i\) peut donc aussi s'écrire \(z=2\left(\cos(\frac{11\pi}{6})+i\sin(\frac{11\pi}{6})\right).\)

Le nombre complexe \(z=i\) peut encore s'écrire \(z=\cos(\frac{\pi}{2})+i\sin(\frac{\pi}{2}).\)  En effet, on calcule

\(|z|=\sqrt{0+1}=1\)

et

\(\cos\phi=\dfrac{0}{1}=0,\qquad\sin\phi=\dfrac{1}{1}=1\qquad\Rightarrow \phi=\dfrac{\pi}{2}.\)

 

Remarque : Deux nombres complexes conjugués ont le même module et des arguments opposés :

\(z=a+bi=|z|(\cos\phi+i\sin\phi)\qquad\textrm{ et}\qquad \bar{z}=a-bi=|z|(\cos(-\phi)+i\sin(-\phi)).\)

(b) Produit de deux nombres complexes

Soient les nombres complexes \(z_1=|z_1|(\cos \phi_1+i\sin \phi_1)\) et \(z_2=|z_2|(\cos \phi_2+i\sin \phi_2)\).  Le produit de deux nombres complexes non nuls a pour module le produit des modules de ces deux nombres complexes et pour argument la somme des arguments de ces nombres complexes :

\(z_1\cdot z_2=|z_1|\, |z_2|\;(\cos (\phi_1+\phi_2)+i\sin (\phi_1+\phi_2)).\)

Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation

Par exemple, pour \(z_1=3\;(\cos(\frac{\pi}{9})+i\sin(\frac{\pi}{9}))\) et \(z_2=\sqrt[]{3}\;(\cos(\frac{7\pi}{18})+i\sin(\frac{7\pi}{18}))\) on a

\(z_1\cdot z_2=3\,\sqrt[]{3}\;(\cos (\frac{\pi}{9}+\frac{7\pi}{18})+i\sin (\frac{\pi}{9}+\frac{7\pi}{18})) =3\,\sqrt[]{3}\;(\cos(\frac{\pi}{2})+i\sin(\frac{\pi}{2})) =3\,\sqrt[]{3}i.\)

(c) Quotient de deux nombres complexes

Soient les nombres complexes \(z_1=|z_1|(\cos \phi_1+i\sin \phi_1)\) et \(z_2=|z_2|(\cos \phi_2+i\sin \phi_2)\).  Le quotient de deux nombres complexes non nuls a pour module le quotient des modules de ces deux nombres et pour argument la différence des arguments de ces deux nombres :

\(\dfrac{z_1}{z_2}= \dfrac{|z_1|}{|z_2|}(\cos(\phi_1-\phi_2)+i\sin(\phi_1-\phi_2)).\)

Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation

Par exemple, pour \(z_1=\cos(\frac{3\pi}{2})+i\sin(\frac{3\pi}{2})\) et \(z_2=2\;(\cos(\frac{\pi}{3})+i\sin(\frac{\pi}{3}))\) on a

\(\dfrac{z_1}{z_2}=\dfrac{1}{2}\;\left(\cos(\frac{3\pi}{2}-\frac{\pi}{3}))+i\sin(\frac{3\pi}{2}-\frac{\pi}{3})\right) =\dfrac{1}{2}\left(\cos(\frac{7\pi}{6})+i\sin(\frac{7\pi}{6})\right) =\dfrac{-\,\sqrt[]{3}}{4}-\dfrac{1}{4}i.\)

 

Inverse d'un nombre complexe

En particulier, si \(z_1=1\), nous avons

\(\dfrac{1}{z_2}=\dfrac{1}{|z_2|}\;(\cos(-\phi_2)+i(-\phi_2)).\)

L'inverse d'un nombre complexe non nul a pour module l'inverse du module de ce nombre et pour argument, l'opposé de l'argument de ce nombre.

(d) Puissance d'un nombre complexe

Soit  \(z=|z|\;(\cos\,\phi+i\sin\,\phi)\)  un nombre complexe et \(n\) un nombre naturel.  En appliquant la règle du produit, nous obtenons

\(z^n=|z|^n\;(\cos(n\phi)+i\sin(n\phi)).\)

Par exemple, calculons \((-1+i)^4\).  On a

\(-1+i=\sqrt[]{2}\;(\cos(\frac{3\pi}{4})+i\sin(\frac{3\pi}{4}))\)

et donc

\((-1+i)^4 =4\;(\cos(\frac{12\pi}{4})+i\sin(\frac{12\pi}{4})) =4\;(\cos\pi+i\sin\pi) =-4.\)

Il s'agit du cas particulier où \(|z|=1\).  En effet, dans ce cas, on a

\(z^n=(\cos(\phi)+i\sin(\phi))^n=\cos(n\phi)+i\sin(n\phi).\)

Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation

Remarque : La formule de Moivre reste valable pour des puissances dont l'exposant est un nombres entier strictement négatif.  En effet, on a

\((\cos\,\phi+i\sin\,\phi)^{-n}=\dfrac{1}{(\cos\,\phi+i\sin\,\phi)^n} =\dfrac{1}{\;(\cos(n\phi)+i\sin(n\phi))} =\;(\cos\,(-n\phi)+i\sin\,(-n\phi)).\)

(e) Racines n^ièmesd'un nombre complexe

Calculer les racines n^ièmes d'un nombre complexe \(r_1\;(\cos\,\phi_1+i\sin\,\phi_1)\) revient à chercher \(z\) tel que \(z^n=r_1\;(\cos\,\phi_1+i\sin\,\phi_1).\)  On obtient \(n\) racines n^ièmes distinctes :

\(z_k=\sqrt[n]{r_1}\left(\cos(\frac{\phi_1+2k\pi}{n})+i\sin(\frac{\phi_1+2k\pi}{n})\right),\qquad k\in \{0,1,2,\cdots n-1\}.\)

Par exemple, calculons les racines sixièmes de \(-64\).  On peut écrire \(-64=64\;(\cos\,\pi+i\sin\,\pi)\) et il reste à résoudre l'équation \(z^6=64\;(\cos\,\pi+i\sin\,\pi).\)  Pour cela, posons \(z=r\;(\cos\,\phi+i\sin\,\phi)\), on a donc

\(r^6\;(\cos(6\phi)+i\sin(6\phi))=64\;(\cos\,\pi+i\sin\,\pi)\)

ce qui implique   \(\left\{\begin{array}{rcl} r^6&=&64\\ 6\phi&=&\pi+2k\pi\quad(k\in\mathbb{Z}) \end{array} \right.\)   et donc   \(\left\{\begin{array}{rcl} r&=&2\\ \phi&=&\dfrac{\pi+2k\pi}{6}\quad(k\in\mathbb{Z}) \end{array} \right.\)

En donnant des valeurs \(\{0,1,2,3,4,5\}\) à \(k\), on trouve les six racines sixièmes de \(-64\) :

\(\begin{array}{ll} z_0=2\;(\cos(\frac{\pi}{6})+i\sin(\frac{\pi}{6}))=\sqrt[]{3}+i&z_3=2\;(\cos(\frac{7\pi}{6})+i\sin(\frac{7\pi}{6}))=-\sqrt[]{3}-i\\[2mm] z_1=2\;(\cos(\frac{\pi}{2})+i\sin(\frac{\pi}{2}))=2i&z_4=2\;(\cos(\frac{3\pi}{2})+i\sin(\frac{3\pi}{2}))=-2i\\[2mm] z_2=2\;(\cos(\frac{5\pi}{6})+i\sin(\frac{5\pi}{6}))=-\sqrt[]{3}+i\hspace{1cm}&z_5=2\;(\cos(\frac{11\pi}{6})+i\sin(\frac{11\pi}{6}))=\sqrt[]{3}-i \end{array}\)

Si on représente ces racines dans le plan de Gauss, on remarque qu'elles forment les sommets d'un hexagone régulier inscrit dans un cercle de centre \((0,0)\) et de rayon \(2=\sqrt[6]{64}\).

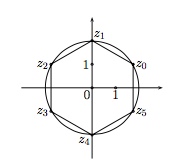
Plus généralement, les racines n^ièmes  du nombre complexe \(r_1\;(\cos\,\phi_1+i\sin\,\phi_1)\) dans le plan de Gauss sont les sommets d'un polygone régulier à \(n\) côtés inscrit dans le cercle de centre \((0,0)\) et de rayon \(\sqrt[n]{r_1}\).

Exponentielle complexe

Ainsi, tout nombre complexe \(z\) non nul peut s'écrire \(z=|z|e^{i\phi}\).  C'est la forme exponentielle d'un nombre complexe \(z\).

On déduit directement de cette définition que le module de \(e^{i\phi}\) est égal à 1 et l'argument de \(e^{i\phi}\) est égal à \(\phi\).

On peut alors écrire sous forme exponentielle, les propriétés rencontrées précédemment.

Lorsque \(\phi=\pi\), nous retrouvons la célèbre formule d'Euler (1707-1783) :

\(e^{i\pi}=-1.\)

En effet, \(e^{i\pi}=\cos \pi+i\sin \pi=-1+i.0=-1\).

Exemples détaillés

1. Calculez \((i-3)(i-2)(i-1)\).

Solution détaillée :  On a

\((i-3)(i-2)(i-1)=(i^2-2i-3i+6)(i-1)=(-5i+5)(i-1)=-5i^2+5i+5i-5=10i\).

 

2. Calculez \((\sqrt[]{3}+i)^2\).

Solution détaillée :  On a

\((\sqrt[]{3}+i)^2=3+2\sqrt{3}i+i^2=3+2\sqrt{3}i-1=2+2\sqrt{3}i\).

 

3. Calculez \(\dfrac{4-i}{2-i}+\dfrac{4+i}{2+i}\).

Solution détaillée :  On a

\(\begin{array}{rcl} \dfrac{4-i}{2-i}+\dfrac{4+i}{2+i}&=&\dfrac{(4-i)(2+i)+(4+i)(2-i)}{(2-i)(2+i)}\\ &=&\dfrac{8+4i-2i-i^2+8+2i-4i-i^2}{4-i^2}\\ &=&\dfrac{16-2i^2}{5}=\dfrac{18}{5} \end{array}\)

 

4. Calculez \(\dfrac{\sqrt[]{3}+i}{\sqrt[]{3}-i}\).

Solution détaillée :  On multiplie haut et bas par le binôme conjugué du dénominateur

\(\dfrac{\sqrt[]{3}+i}{\sqrt[]{3}-i}=\dfrac{(\sqrt[]{3}+i)^2}{(\sqrt[]{3}-i)(\sqrt[]{3}+i)}=\dfrac{3+2\sqrt{3}i+i^2}{3-i^2}=\dfrac{2+2\sqrt{3}i}{4}=\dfrac{1+\sqrt{3}i}{2}\).

 

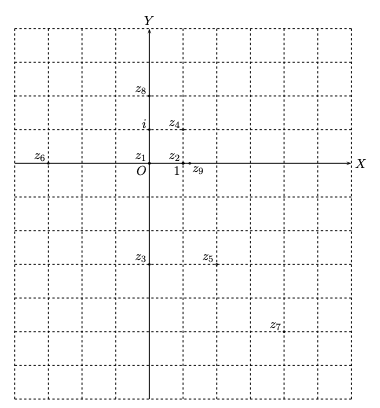
5. Représentez dans le plan de Gauss les nombres complexes suivants : \(z_1=0,\, z_2=1,\, z_3=-3i,\, z_4=1+i,\, z_5=2-3i,\, z_6=-3,\, z_7=(3-2i)+(1-3i),\, \\ z_8=(1+i)-(1-i),\, z_9=\dfrac{2i-1}{2i+1}+\dfrac{2i+1}{2i-1},\, z_{10}=(i+1)(i+2)-(i+3)(i+4).\)

Solution détaillée :  On a \(z_1=(0,0),\, z_2=(1,0),\, z_3=(0,-3),\, z_4=(1,1),\, z_5=(2,-3),\, z_6=(-3,0),\, \\ z_7=(3-2i)+(1-3i)=4-5i=(4,-5),\, z_8=(1+i)-(1-i)=0+2i=(0,2),\, \\ z_9=\dfrac{2i-1}{2i+1}+\dfrac{2i+1}{2i-1}=\dfrac{(2i-1)^2+(2i+1)^2}{(2i+1)(2i-1)}=\dfrac{-6}{-5}=(\frac{6}{5},0),\, \\ z_{10}=(i+1)(i+2)-(i+3)(i+4)=(3i+1)-(7i+11)=-4i-10=(-10,-4).\)

 

6. Calculez les racines carrées du nombre complexe \(\dfrac{1}{2}+\dfrac{\sqrt[]{3}}{2}i\).

Solution détaillée :  On résoud l'équation \(z^2=\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i\) où \(z=x+yi\) (avec \(x\) et \(y\in\mathbb{R}\)) et  on utilise la propriété \(|z^2|=|z|^2\):

\(\left\{\begin{array}{l} x^2-y^2=\dfrac{1}{2}\\ 2xy=\dfrac{\sqrt{3}}{2}\\ x^2+y^2=\sqrt{\dfrac{1}{4}+\dfrac{3}{4}} \end{array}\right. \quad\iff\left\{\begin{array}{l} x^2-y^2=\dfrac{1}{2}\\ x^2+y^2=1\\ xy=\dfrac{\sqrt{3}}{4} \end{array}\right. \quad\iff\left\{\begin{array}{l} 2x^2=\dfrac{3}{2}\\ 2y^2=\dfrac{1}{2}\\ xy=\dfrac{\sqrt{3}}{4} \end{array}\right.\\ \iff\left\{\begin{array}{l} x^2=\dfrac{3}{4}\\[2mm] y^2=\dfrac{1}{4}\\[2mm] xy=\dfrac{\sqrt{3}}{4} \end{array}\right. \quad\iff\left\{\begin{array}{l} x=\pm \dfrac{\sqrt{3}}{2}\\ y=\pm \dfrac{1}{2}\\ xy=\dfrac{\sqrt{3}}{4} \quad\textrm{(positif donc $x$ et $y$ de même signe)} \end{array}\right.\)

Les solutions sont \(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\)  et  \(-\dfrac{\sqrt{3}}{2}-\dfrac{1}{2}i\).

 

7. Résolvez l'équation \(x^2+x+1=0\).

Solution détaillée :  On calcule \(\Delta=1-4\cdot 1\cdot 1=-3\) et donc \(\sqrt[]{\Delta}=\pm\sqrt{3}i\).  On obtient

\(x_1=\dfrac{-1+\sqrt{3}i}{2}\) et \(x_2=\dfrac{-1-\sqrt{3}i}{2}\).

 

8. Résolvez l'équation \(ix^2-(5i+2)x+5(i+1)=0\).

Solution détaillée :  On calcule

\(\Delta=(5i+2)^2-4\cdot i\cdot 5(i+1)=25i^2+4+20i-20i^2-20i=-1\)

et donc \(\sqrt[]{\Delta}=\pm i\). 

On obtient  \(x_1=\dfrac{5i+2+i}{2i}=\dfrac{6i+2}{2i}=\dfrac{(3i+1)(-i)}{1} =3-i\)

et  \(x_2=\dfrac{5i+2-i}{2i} =\dfrac{4i+2}{2i} =\dfrac{(2i+1)(-i)}{1} =2-i\).

Les deux solutions de l'équation sont donc \(3-i\) et \(2-i\).

 

9. Calculez la partie réelle et la partie imaginaire du nombre complexe \(z_1=\dfrac{z^2+z+1}{z^4-1}\) si \(z=2+3i\).

Solution détaillée :  On calcule \(z^2=(2+3i)^2=4+12i+9i^2=12i-5\) et \(z^4=(12i-5)^2=144i^2-120i+25=-119-120i\) et on remplace dans \(z_1\) :

\(\begin{array}{rcl} z_1&=&\dfrac{z^2+z+1}{z^4-1}=\dfrac{(12i-5)+(2+3i)+1}{(-119-120i)-1}\\ &=&\dfrac{15i-2}{-120-120i}=\dfrac{15i-2}{-120(1+i)}\\ &=&\dfrac{(15i-2)(1-i)}{-120(1+i)(1-i)}=\dfrac{17i+13}{-240}=\dfrac{-13}{240}-\dfrac{17}{240}i \end{array}\)

La partie réelle est donc \(\dfrac{-13}{240}\) et la partie imaginaire est \(\dfrac{-17}{240}\).

 

10. Décomposez Le polynôme \(z^4+2z^3+3z^2+4z+2\)  en produit de polynômes du premier degré à coefficients complexes.

Solution détaillée :  \(P(z)=z^4+2z^3+3z^2+4z+2\)

\(P(-1)=1-2+3-4+2=0\) donc \(P(z)\) est divisible par \((z+1)\).  En utilisant la Règle de Horner, on obtient

\(\begin{array}{c|cccc|c} &1&2&3&4&2\\ -1&&-1&-1&-2&-2\\ \hline &1&1&2&2&0 \end{array}\)

 \(P(z)=(z+1)(z^3+z^2+2z+2)\)

Factorisons \(z^3+z^2+2z+2\) : \(P(-1)=-1+1-2+2=0\) donc \(P(z)\) est divisible par \((z+1)\)

\(\begin{array}{c|ccc|c} &1&1&2&2\\ -1&&-1&0&-2\\ \hline &1&0&2&0 \end{array}\)

\(P(z)=(z+1)^2(z^2+2)=(z+1)^2(z-\sqrt{2}i)(z+\sqrt{2}i)\).

 

11. Soit le polynôme \(P(x)=x^4+4x^3+8x^2+4x+7\).

    1. Calculez \(P(i)\).
    2. Ecrivez \(P(x)\) sous la forme d'un produit de deux polynômes du deuxième degré à coefficients réels.
    3. Calculez les racines de l'équation \(P(x)=0\). 

Solution détaillée : 

1. On remplace \(x\) par \(i\) dans le polynôme :  \(P(i)=i^4+4i^3+8i^2+4i+7=1+4(-i)+8(-1)+4i+7=1-4i-8+4i+7=0\)
2. Comme \(P(i)=0\), \(P(x)\) est divisible par \((x-i)\) et comme \(P(-i)=0\), \(P(x)\) est divisible par \((x+i)\).  On en déduit que \(P(x)\) est divisible par \((x-i)(x+i)\), c'est-à-dire par \(x^2+1\).

En effectuant la division euclidienne de \(x^4+4x^3+8x^2+4x+7\) par \(x^2+1\) on obtient \(x^2+4x+7\) et donc  \(P(x)=(x^2+1)(x^2+4x+7)\).

3.  \(P(x)=0 \iff (x^2+1)(x^2+4x+7)=0\)

\(\begin{array}{c} x^2+1=0\\ x^2=-1\\ x=\pm i \end{array}\hspace{1cm} \begin{array}{c} x^2+4x+7=0\\ \Delta = -12 \\ x=\dfrac{-4\pm 2\sqrt{3}i}{2}=-2\pm \sqrt{3}i \end{array}\)

Les solutions sont donc \(-i,i,-2-\sqrt{3}i \mbox{ et }-2+\sqrt{3}i \).

 

12. Ecrivez le nombre complexe \(z=1+\sqrt{3}i\) sous forme trigonométrique.

Solution détaillée : On calcule le module \(|z|=\sqrt{a^2+b^2}\) et l'argument \(\phi\) tel que \(\cos \phi =\dfrac{a}{|z|}\) et \(\sin \phi =\dfrac{b}{|z|}\) :

\(|z|=\sqrt[]{1+3}=2\)

\(\cos\phi=\dfrac{1}{2}\qquad\sin\phi=\dfrac{\sqrt{3}}{2}\qquad\Rightarrow \phi=\dfrac{\pi}{3}+2k\pi\qquad (k\in\mathbb{Z})\)

Une forme trigonométrique de \(z\) est donc \(2(\cos \frac{\pi}{3} +i\sin \frac{\pi}{3})\).

 

13. Calculez le module et l'argument principal du nombre complexe \(z=\dfrac{1-\sqrt[]{3}i}{2i}\).

Solution détaillée : On calcule le module et l'argument du numérateur et du dénominateur séparément puis on applique les règles de calcul : \(|z|=\dfrac{r_1}{r_2}\) et \(\phi=\phi_1-\phi_2\).

Soit \(z_1=1-\sqrt{3}i\) : \(r_1=2\); \(\cos\phi_1=\dfrac{1}{2}\) et \(\sin\phi_1=-\dfrac{\sqrt{3}}{2}\) donc \(\phi_1=-\dfrac{\pi}{3}\).

Soit \(z_2=2i\) : \(r_2=2\); \(\cos\phi_2=0\) et \(\sin\phi_2=1\) donc \(\phi_2=\dfrac{\pi}{2}\).

On en déduit \(|z|=\dfrac{r_1}{r_2}=1\)  et  \(\phi=\phi_1-\phi_2=-\dfrac{\pi}{3}-\dfrac{\pi}{2}=\dfrac{-5\pi}{6}\).

 

14. Calculez le module et l'argument principal du nombre complexe \(z=(1-i)^2(\sqrt[]{3}-i)^3\).

Solution détaillée : On calcule le module et l'argument des différents facteurs et on applique les règles de calcul des opérations sur les nombres complexes sous forme trigonométrique.

On a \(z_1=1-i\) donc  \(r_1=\sqrt{2}\) , \(z_2=\sqrt{3}-i\) donc  \(r_2=2\) .

On obtient \(|z|=r_1^2\cdot r_2^3=2\cdot 8=16\).

On a \(z_1=1-i\) :   \(\cos\phi_1=\dfrac{\sqrt{2}}{2}\) , \(\sin\phi_1=-\dfrac{\sqrt{2}}{2}\) donc \(\phi_1=-\dfrac{\pi}{4}\).

\(z_2=\sqrt{3}-i\) :  \(\cos\phi_2=\dfrac{\sqrt{3}}{2}\), \(\sin\phi_2=\dfrac{-1}{2}\)  donc \(\phi_2=\dfrac{-\pi}{6}\).

On obtient \(\phi=2\phi_1+3\phi_2=2(\frac{-\pi}{4})+3(\frac{-\pi}{6})=-\pi\mbox{ ou }\pi\).

 

15. Calculez le module et l'argument principal du nombre complexe \(z=\dfrac{(\sqrt[]{3}-i)^3(1-i)^4}{i^7(1+i)^6}\).

Solution détaillée : On calcule le module et l'argument des différents facteurs et on applique les règles de calcul des opérations sur les nombres complexes sous forme trigonométrique.

On a \(z_1=\sqrt{3}-i\) donc  \(r_1=2\) , \(z_2=1-i\) donc  \(r_2=\sqrt{2}\) ,   \(z_3=i\) donc  \(r_3=1\) et  \(z_4=1+i\)  donc \(r_4=\sqrt{2}\) .

On obtient \(|z|=\dfrac{r_1^3\cdot r_2^4}{r_3^7\cdot r_4^6}=\dfrac{2^3\cdot (\sqrt{2})^4}{1^7\cdot (\sqrt{2})^6}=4\).

On a  \(z_1=\sqrt{3}-i\) :   \(\cos\phi_1=\dfrac{\sqrt{3}}{2}\) , \(\sin\phi_1=-\dfrac{1}{2}\) donc \(\phi_1=-\dfrac{\pi}{6}\).

\(z_2=1-i\) :     \(\cos\phi_2=\dfrac{\sqrt{2}}{2}\), \(\sin\phi_2=-\dfrac{\sqrt{2}}{2}\)  donc \(\phi_2=\dfrac{-\pi}{4}\).

\(z_3=i\) :     \(\cos\phi_3=0\), \(\sin\phi_3=1\)  donc \(\phi_3=\dfrac{\pi}{2}\).

\(z_4=1+i\) :     \(\cos\phi_4=\dfrac{\sqrt{2}}{2}\), \(\sin\phi_4=\dfrac{\sqrt{2}}{2}\)  donc \(\phi_4=\dfrac{\pi}{4}\).

On obtient

\(\begin{array}{rcl} \phi&=&(3\phi_1+4\phi_2)-(7\phi_3+6\phi_4)\\ &=&(3(-\frac{\pi}{6})+4(\frac{-\pi}{4}))-(7(\frac{\pi}{2})+6(\frac{\pi}{4}))\\ &=&\dfrac{-13\pi}{2}=\dfrac{-\pi}{2} \end{array}\).

 

16. Résolvez l'équation \(z^3=8i\).

 Solution détaillée : On va mettre le nombre \(8i\) sous forme trigonométrique \(8i=r_1(\cos\phi_1+i\sin\phi_1)\) en recherchant \(r_1\) et \(\phi_1\) puis on résoud l'équation \(z^3=r_1(\cos\phi_1+i\sin\phi_1)\) où \(z=r(\cos\phi+i\sin\phi)\).

\(8i=r_1(\cos\phi_1+i\sin\phi_1)\) donc \(r_1=8\) et \(\cos\phi_1+i\sin\phi_1=i\) donc \(\phi_1=\dfrac{\pi}{2}\).

Résolvons l'équation \(z^3=8(\cos\frac{\pi}{2}+i\frac{\pi}{2})\) où \(z=r(\cos\phi+i\sin\phi)\).

On a donc \(r^3(\cos3\phi+i\sin3\phi)=8(\cos\frac{\pi}{2}+i\frac{\pi}{2})\)

Et par suite,

\(\left\{\begin{array}{rl} r^3&=8\\ 3\phi&=\dfrac{\pi}{2}+2k\pi\quad(k\in\mathbb{Z}) \end{array} \right.\qquad \left\{\begin{array}{rl} r&=2\\ \phi&=\dfrac{\dfrac{\pi}{2}+2k\pi}{3}\quad(k\in\mathbb{Z}) \end{array} \right.\)

En donnant des valeurs \(\{0,1,2\}\) à \(k\), il vient

\(z_0=2\;(\cos\,\,\frac{\pi}{6}+i\sin\,\,\frac{\pi}{6})=\sqrt[]{3}+i\)

\(z_1=2\;(\cos\,\frac{5\pi}{6}+i\sin\,\frac{5\pi}{6})=-\sqrt[]{3}+i\)

\(z_2=2\;(\cos\,\frac{9\pi}{6}+i\sin\frac{9\pi}{6})=-2i\)

 

17. Résolvez l'équation \(z^5=2-2i\).

 Solution détaillée : On va mettre le nombre \(2-2i\) sous forme trigonométrique  \(2-2i=r_1(\cos\phi_1+i\sin\phi_1)\) en recherchant \(r_1\) et \(\phi_1\) puis on résoud l'équation  \(z^5=r_1(\cos\phi_1+i\sin\phi_1)\) où \(z=r(\cos\phi+i\sin\phi)\).

\(2-2i=r_1(\cos\phi_1+i\sin\phi_1)\), \(r_1=2\sqrt{2}\), \(\cos\phi_1=\dfrac{\sqrt{2}}{2}\) et \(\sin\phi_1=\dfrac{-\sqrt{2}}{2}\) donc \(\phi_1=\dfrac{-\pi}{4}\).

Résolvons l'équation \(z^5=2\sqrt{2}(\cos\frac{-\pi}{4}+i\sin\frac{-\pi}{4})\) où \(z=r(\cos\phi+i\sin\phi)\).

On a \(r^5(\cos5\phi+i\sin5\phi)=2\sqrt{2}(\cos\frac{-\pi}{4}+i\sin\frac{-\pi}{4})\)

et par suite,

\(\left\{\begin{array}{rl} r^5&=2\sqrt{2}\\ 5\phi&=\dfrac{-\pi}{4}+2k\pi\quad(k\in\mathbb{Z}) \end{array} \right. \qquad \left\{\begin{array}{rl} r&=\sqrt[5]{2\sqrt{2}}=\sqrt[10]{8}\\ \phi&=\dfrac{\dfrac{-\pi}{4}+2k\pi}{5}\qquad(k\in\mathbb{Z}) \end{array} \right.\)

En donnant des valeurs \(\{0,1,2,3,4\}\) à \(k\), il vient

\(z_0=\sqrt[10]{8}\;(\cos\,\,\frac{-\pi}{20}+i\sin\,\,\frac{-\pi}{20})\)

\(z_1=\sqrt[10]{8}\;(\cos\,\frac{7\pi}{20}+i\sin\,\frac{7\pi}{20})\)

\(z_2=\sqrt[10]{8}\;(\cos\,\frac{3\pi}{4}+i\sin\frac{3\pi}{4})\)

\(z_3=\sqrt[10]{8}\;(\cos\,\frac{23\pi}{20}+i\sin\,\frac{23\pi}{20})\)

\(z_4=\sqrt[10]{8}\;(\cos\,\frac{31\pi}{20}+i\sin\,\frac{31\pi}{20})\)

qui sont les cinq racines cinquièmes de \(2-2i\).

Preuves