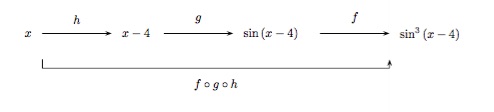Théorie du module : Fonctions
Table des matières
- Définitions
- Représentation graphique
- Propriétés
- Fonctions élémentaires
- Opérations sur les fonctions
- Exemples détaillés
Définitions
Les fonctions sont les objets de base traités en calcul différentiel et intégral. Ce chapitre est une introduction à cette matière en ce qu'il examine les premiers éléments qui regardent les fonctions, leur représentation graphique, des façons de les transformer et de les composer.
Il y a fonction dès qu'une quantité dépend d'une autre.
Voici quatre situations.
- L'aire \(A\) d'un cercle dépend du rayon \(r\) de ce cercle. C'est l'équation \(A=\pi r^2\) qui exprime la règle qui lie \(r\) et \(A\). A chaque valeur positive de \(r\) est associée une valeur de \(A\), on dit que \(A\) est une fonction de \(r\).
- La population mondiale \(P\) dépend du temps \(t\). La table ci-contre donne une estimation de cette population mondiale \(P(t)\) au temps \(t\), pour quelques années. Par exemple, \(P(1950)\approx 2\,520\,000\,000.\)
\(\begin{array} {|c|c|} \hline \mbox{Année}&\mbox{Population} \\ &\mbox{(en millions)}\\ \hline 1900&1650\\ 1910&1750\\ 1920&1860\\ 1930&2070\\ 1940&2300\\ 1950&2520\\ 1960&3020\\ 1970&3700\\ 1980&4450\\ 1990&5300\\ 1996&5770\\ \hline \end{array}\)
Mais à chaque valeur de la variable t correspond une valeur de P et on dit que P est une fonction de t.
- Le coût \(C\) d'affranchissement d'une lettre dépend de son poids \(p \). Bien qu'il n'existe pas de formule simple qui lie \(C\) et \(p \), le bureau postal dispose d'un tarif qui lui permet de déterminer \(C\) dès que \(p \) est connu.
- L'accélération verticale \(a\) du sol telle qu'elle est mesurée par un séismographe durant un tremblement de terre est une fonction du temps. On peut y lire la valeur de \(a\) correspondant à un certain moment \(t\) choisi.
Chacun de ces exemples décrit une règle selon laquelle, à un nombre (\(r\), \(t\), \(p \) ou \(t\)), est associé un autre nombre (\(A\), \(P\), \(C\) ou \(a\)). Dans chaque cas, on dit que le deuxième nombre est une fonction du premier.
Définition - Une fonction \(f\) est une règle qui assigne à chaque élément \(x\) d'un ensemble \(A\) exactement un élément, noté \(f(x)\), d'un ensemble \(B\).
Les ensembles \(A\) et \(B\) envisagés pour des fonctions sont habituellement des ensembles de nombres. L'ensemble \(A\) est appelé le domaine de définition de la fonction. Le nombre \(f(x)\) est la valeur de \(f\) en \(x\) et se lit "\(f\) de \(x\)". L'ensemble de toutes les valeurs \(f(x)\) possibles lorsque \(x\) parcourt tout le domaine de définition s'appelle l'ensemble image. On appelle variable indépendante un symbole qui peut prendre une valeur quelconque du domaine de définition de la fonction \(f\). On appelle variable dépendante un symbole qui prend une valeur de l'ensemble image de \(f\).
Reprenons les 4 situations précédentes.
- Le rayon \(r\) est la variable indépendante et l'aire du disque de rayon \(r\), \(A(r)\), est la variable dépendante.
- Le temps \(t\) est la variable indépendante et la population mondiale \(P(t)\) est la variable dépendante.
- Le poids \(p \) est la variable indépendante et le coût \(C(p)\) est la variable dépendante.
- Le temps \(t\) est la variable indépendante et l'accélération \(a(t)\) est la variable dépendante.
On écrira aussi bien \(f(x)=x^2\) ou \(f(t)=t^2\) ou \(f(r)=r^2\) pour exprimer la fonction qui consiste à élever un nombre réel au carré.
Il est instructif de comparer une fonction à une espèce de machine. Lorsque \(x\) est une valeur du domaine de définition de la fonction \(f\), alors la machine l'accepte comme entrée et produit à la sortie \(f(x)\), selon la règle qui définit la fonction. Dès lors, le domaine de définition peut être vu comme l'ensemble de toutes les entrées possibles de la machine et l'ensemble image, comme l'ensemble des sorties possibles.
Les fonctions préprogrammées des calculatrices illustrent fort bien la notion de fonction regardée comme une machine. Prenons l'exemple de la fonction activée par la touche \(\sqrt x\) de votre calculatrice. D'abord, vous entrez \(x\). Ensuite, vous pressez la touche \(\sqrt x\). Si \(x<0\), il n'appartient pas au domaine de définition de la fonction et, de ce fait, ne sera pas accepté par la calculatrice, qui du reste vous enverra un message d'erreur. Par contre, si \(x\ge 0\), la calculatrice affichera une valeur approximative de \(\sqrt x\). La touche \(\sqrt x\) de votre calculatrice n'est donc pas tout à fait la même chose que la fonction mathématique définie par \(f(x)=\sqrt x\).
Représentation graphique
En général, les représentations graphiques de fonctions sont réalisées dans un repère cartésien orthonormé. On représente la variable indépendante sur l'axe horizontal (appelé axe \(OX\)) et la variable dépendante sur l'axe vertical (appelé axe \(OY\)).
\(G_f=\{(x,f(x))\quad |\quad x\in A\}\)
(il s'agit des couples entrée/sortie).
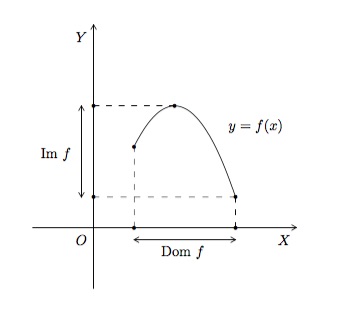
Autrement dit, le graphique de \(f\) est constitué de l'ensemble des points \((x,y)\) du plan de coordonnées tels que \(y=f(x)\) et \(x\) appartient au domaine de définition de \(f\). La représentation graphique d'une fonction \(f\) nous donne une image intéres\-sante du comportement d'une fonction. Comme, en chaque point \((x,y)\) de la courbe, l'ordonnée \(y\) est égale à la valeur de \(f(x)\), elle peut être lue comme la hauteur de la courbe au point \(x\). Pour trouver les points d'ordonnée \(c\), il suffit donc de tracer la droite \(y=c\) et de regarder ses intersections avec le graphe de la fonction.
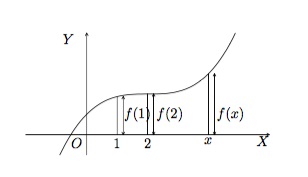
La représentation graphique de \(f\) nous permet aussi de visualiser le domaine de définition et l'ensemble image de f sur les axes \(OX\) et \(OY\) respectivement.
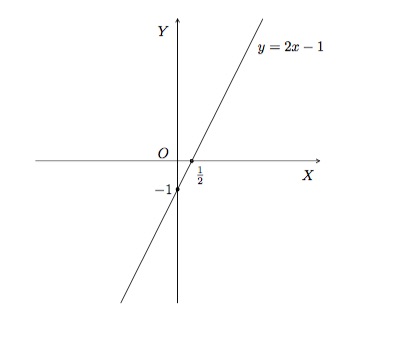
Dessinons la courbe représentative de la fonction \(f(x)=2x-1\). L'équation de la courbe est \(y=2x-1\) et nous y reconnaissons celle d'une droite de pente 2 et d'ordonnée à l'origine \(-1\). Comme l'expression \(2x-1\) est définie pour toutes les valeurs réelles de \(x\), le domaine de définition de \(f\) est tout l'ensemble des nombres réels, noté \(\mathbb{R}\). Le graphique montre que l'ensemble image est aussi \(\mathbb{R}\).
Cherchons le domaine de définition de la fonction \(f(x)=\sqrt{x+2}\). Comme la racine carrée d'un nombre négatif n'est pas définie (en tant que nombre réel), le domaine de définition de \(f\) ne comprend que les valeurs de \(x\) pour lesquelles \(x+2\ge0\). Ce qui est équivalent à \(x\ge -2\). Le domaine de définition est donc l'intervalle \([-2;+\infty[\).
La représentation graphique d'une fonction est une courbe du plan \(OXY\). Pour déterminer les courbes du plan qui sont le graphe d'une fonction, nous pouvons utiliser le test suivant.
En effet, si une droite verticale quelconque \(x=a\) ne coupe une courbe qu'une fois, en \((a,b)\), alors une seule image \(b\) est associée à \(a\) par \(f\). Si au contraire, une droite \(x=a\) coupe une courbe deux fois, en \((a,b)\) et en \((a,c)\), alors cette courbe ne peut être la représentation d'une fonction car une fonction ne peut attribuer deux valeurs différentes à \(a\).
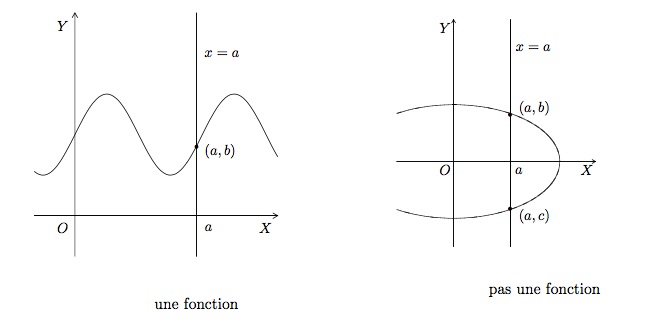
Dans un graphique, on remarque quelques points particuliers.
Une racine est l'abscisse du point d'intersection du graphe avec l'axe \(OX\). Pour trouver les racines, il faut donc résoudre l'équation \(f(x)=0\).
L'ordonnée à l'origine est l'ordonnée du point d'intersection du graphe avec l'axe \(OY\). Pour la trouver, on remplace \(x\) par \(0\) dans la formule de \(f\), c'est-à-dire on calcule \(f(0)\).
Pour déterminer le signe d'une fonction, il faut résoudre les inéquations \(f(x)<0\) et \(f(x)>0\).
Pour un rappel concernant les tableaux de signes, cliquez ici.
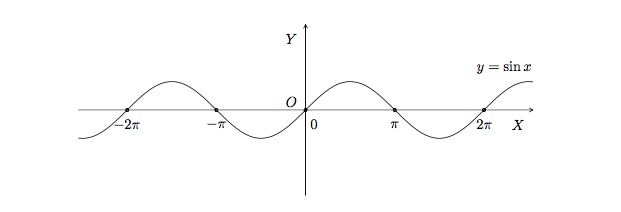
Regardons la fonction \(f(x)=\sin{x}\) sur l'intervalle \([-2\pi,2\pi]\).
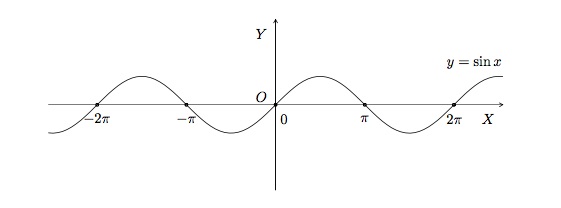
Cette fonction possède 5 racines : \(x=-2\pi\), \(x=-\pi\), \(x=0\), \(x=\pi\) et \(x=2\pi\). Son ordonnée à l'origine est \(y=0\). Elle est positive pour \(x\in\, ]-2\pi,2\pi[\, \) et \(x\in\, ]0,\pi[\, \) et elle est négative pour \(x\in\, ]-\pi,0[\, \) et \(x\in\, ]\pi,2\pi[\, \).
La valeur \(f(m)\) est le minimum (ou valeur minimale) de la fonction \(f\) sur l'intervalle \(I\) si pour tout \(x\in I\), on a \(f(x)\geq f(m)\).
Graphiquement, le maximum correspont à la plus grande valeur d'une fonction et le minimum correspond à la plus petite valeur.
La fonction \(f(x)=\sin{x}\) sur l'intervalle \([-2\pi,2\pi]\), représentée ci-dessus, a un maximum \(y=1\) et un minimum \(y=-1\). Les valeurs maximales sont atteintes pour \(x=-\frac{3\pi}{2}\) et \(x=\frac{\pi}{2}\) et les valeurs minimales sont atteintes pour \(x=-\frac{\pi}{2}\) et \(x=\frac{3\pi}{2}\).
Propriétés
(a) Fonctions croissantes/décroissantes
On dit que la fonction est strictement croissante sur l'intervalle \([a,b]\) si la courbe représentant la fonction monte sur cet intervalle; elle est strictement décroissante sur l'intervalle \([a,b]\) si la courbe descend sur cet intervalle.
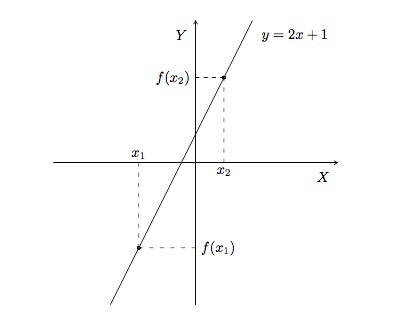
Définitions - Une fonction \(f\) est dite strictement croissante sur un intervalle \(I\) si pour tout \(x_1\), \(x_2\in I\), on a
\(x_1<x_2\Rightarrow f(x_1)<f(x_2).\)
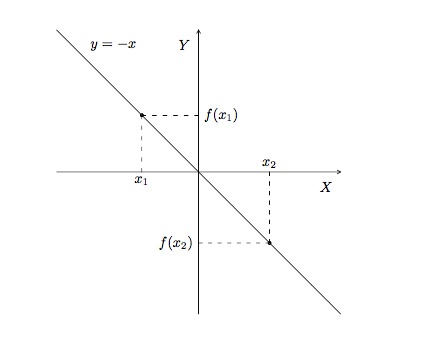
Une fonction \(f\) est dite strictement décroissante sur un intervalle \(I\) si pour tout \(x_1\), \(x_2\in I\), on a
\(x_1<x_2\Rightarrow f(x_1)>f(x_2).\)
Une fonction \(f\) est dite monotone sur un intervalle \(I\) si elle est soit croissante, soit décroissante sur \(I\).
L'élément important dans cette définition est que l'inégalité \(f(x_1)<f(x_2)\) doit être satisfaite pour toute paire de points \(x_1\) et \(x_2\) de \(I\) qui sont tels que \(x_1<x_2\).
La fonction \(f(x)= 2x+1\) est une fonction strictement croissante. En effet, si \(x_1\), \(x_2\in\mathbb{R}\) avec \(x_1<x_2\), on a \(2x_1<2x_2\) et \(2x_1+1<2x_2+1\). Donc \(f(x_1)<f(x_2)\).
La fonction \(f(x)= -x\) est une fonction strictement décroissante. En effet, si \(x_1\), \(x_2\in\mathbb{R}\) avec \(x_1<x_2\), on a \(-x_1>-x_2\), donc \(f(x_1)>f(x_2)\).
La fonction \(f(x)=\sin{x}\) n'est ni croissante, ni décroissante sur \([-2\pi,2\pi]\). En effet, on remarque sur le graphe que la courbe monte sur certains intervalles et descend sur d'autres.
(b) Fonctions paires/impaires
Définitions - Soit \(f\), une fonction définie sur un intervalle \(I\).
La fonction \(f\) est paire si pour tout \(x\in I\), on a
\(-x\in I\mbox{ et }f(-x)=f(x).\)
La fonction \(f\) est impaire si pour tout \(x\in I\), on a
\(-x\in I\mbox{ et }f(-x)=-f(x).\)
La fonction \(f(x)=x^2\) est une fonction paire car elle est définie sur \(\mathbb{R}\) tout entier et pour tout \(x\), on a \(f(-x)=(-x)^2=x^2=f(x).\)
La fonction \(f(x)=x^3\) est impaire car elle est définie sur \(\mathbb{R}\) tout entier et pour tout \(x\), on a \(f(-x)=(-x)^3=-x^3=-f(x).\)
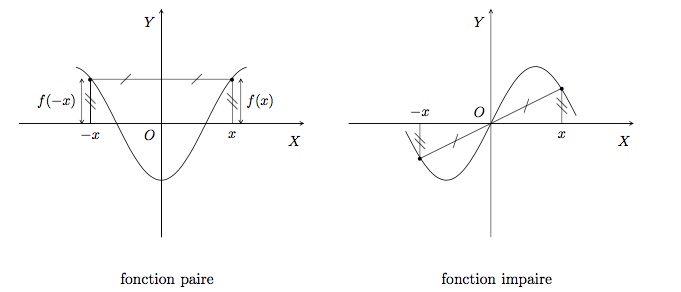
Graphiquement, on reconnaît une fonction paire par une symétrie de son graphique par rapport à l'axe \(OY\). En effet, les ordonnées de 2 points du graphe d'abscisses opposées sont égales. Ce qui signifie qu'ayant déjà dessiné le graphique de \(f\) pour \(x\ge 0\), nous l'obtenons tout entier en lui ajoutant simplement l'image symétrique par rapport à l'axe \(OY\).
Le graphique d'une fonction impaire est symétrique par rapport à l'origine. En effet, les ordonnées de 2 points du graphe d'abscisses opposées sont également opposés. Si nous avons déjà dessiné le graphique de \(f\) pour \(x\ge 0\), nous l'obtenons tout entier en lui adjoignant simplement l'image obtenue après une rotation de \(180^\circ\) autour de l'origine.
La fonction \(f(x)=x^5+x\) est impaire. En effet, pour tout \(x\in\mathbb{R}\), on a \(-x\in\mathbb{R}\) et
\(\begin{array}{lll} f(-x)&=&(-x)^5+(-x)=(-1)^5x^5+(-x)\\ &=&-x^5-x=-(x^5+x)\\ &=&-f(x). \end{array}\)
(c) Fonctions périodiques
La fonction \(f\) est périodique de période \(p\) si pour tout \(x\in D\), on a
\(f(x+p)=f(x).\)
La fonction \(f(x)=\sin{x}\) est périodique de période \(2\pi\). La fonction \(f(x)=\tan{x}\) est périodique de période \(\pi\).
Fonctions élémentaires
(a) Fonction constante
La fonction constante \(f(x)=c\) est définie sur \(\mathbb{R}\) et son ensemble image est réduit au seul nombre \(c\). Son graphique est une droite horizontale.
(b) Fonction identité
La fonction identité \(f(x)=x\) est définie sur \(\mathbb{R}\) et son ensemble image est \(\mathbb{R}\). Son graphe est constitué de l'ensemble des couples \((x,y)\) où \(y=x\). Comme ces points sont à égale distance des deux axes, ils appartiennent à la bissectrice des axes.
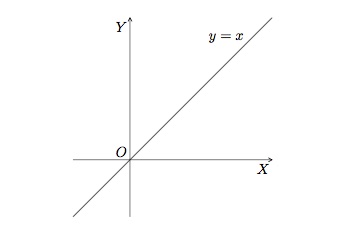
Cette fonction a une racine \(x=0\) et son ordonnée à l'origine est \(y=0\). Elle est positive pour les valeurs de \(x\) positives et négative pour les valeurs de \(x\) négatives. Elle est impaire et strictement croissante sur \(\mathbb{R}\). Elle n'a ni minimum, ni maximum.
(c) Fonction valeur absolue
La fonction valeur absolue \(f(x)=|x|\) est définie sur \(\mathbb{R}\) et son ensemble image est \(\mathbb{R}^+\). Son graphe est constitué de l'ensemble des couples \((x,y)\) où \(y=|x|\).
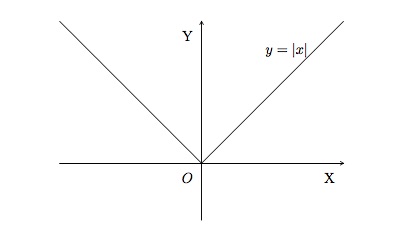
Cette fonction a une racine \(x=0\) et son ordonnée à l'origine est \(y=0\). Elle est toujours positive et nulle en \(0\). Elle est paire et strictement croissante sur \(\mathbb{R}^+\), strictement décroissante sur \(\mathbb{R}^-\). Elle a un minimum en \(x=0\) et pas de maximum.
Cliquez sur le lien pour un rappel des propriétés de la valeur absolue.
(d) Fonctions puissances
Une fonction de la forme \(f(x)=x^{a}\), où \(a\) est une constante, est appelée une fonction puissance. Nous envisageons plusieurs cas.
- \(a=0\). On retrouve la fonction constante \(f(x)=x^0=1\).
- \(a=1\). On retrouve la fonction identité \(f(x)=x\).
- \(a=2\). La fonction du second degré \(f(x)=x^2\) est définie sur \(\mathbb{R}\) et son ensemble image est \(\mathbb{R}^+\). Son graphe est l'ensemble des couples \((x,y)\) où \(y=x^2\).
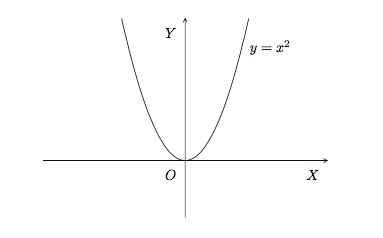
Cette fonction a une racine \(x=0\) et son ordonnée à l'origine est \(y=0\). Elle est toujours positive et nulle en \(0\). Elle est paire et strictement croissante sur \(\mathbb{R}^+\), strictement décroissante sur \(\mathbb{R}^-\). Elle a un minimum en \(x=0\) et pas de maximum.
- \(a=3\). La fonction du troisième degré \(f(x)=x^3\) est définie sur \(\mathbb{R}\) et son ensemble image est \(\mathbb{R}\). Son graphe est l'ensemble des couples \((x,y)\) où \(y=x^3\).
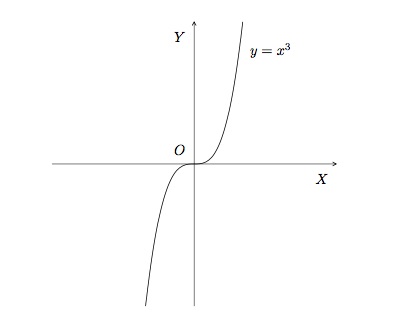
Cette fonction a une racine \(x=0\) et son ordonnée à l'origine est \(y=0\). Elle est positive pour les valeurs de \(x\) positives et négative pour les valeurs de \(x\) négatives. Elle est impaire et strictement croissante sur \(\mathbb{R}\). Elle n'a ni minimum, ni maximum.
- \(a=n\), \(n\in\mathbb{N}_0\). L'allure générale du graphique de \(f(x)=x^n\) change selon que \(n\) est un nombre pair ou impair. Lorsque \(n\) est pair, la fonction \(f(x)=x^n\) est paire et son graphique ressemble à la parabole \(y=x^2\). Lorsque \(n\) est impair, \(f(x)=x^n\) est une fonction impaire et son graphique a la même allure que \(y=x^3\).
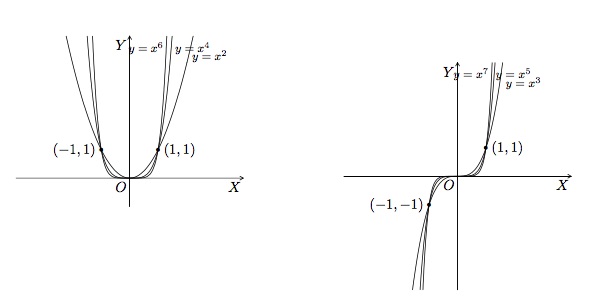
Cliquez sur le lien pour un rappel concernant les propriétés des puissances.
- \(a=-1\). La fonction inverse \(f(x)=\frac{1}{x}\) est définie sur \(\mathbb{R}_0\) et son ensemble image est \(\mathbb{R}_0\) . Son graphe est une hyperbole équilatère dont les axes de coordonnées sont les asymptotes.
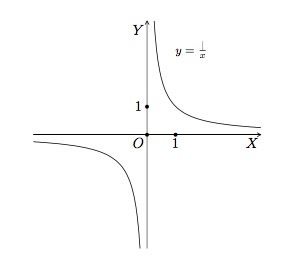
Cette fonction n'a pas de racine ni d'ordonnée à l'origine. Elle est positive pour les valeurs de \(x\) positives et négative pour les valeurs de \(x\) négatives. Elle est impaire et strictement croissante sur \(\mathbb{R}^+_0\), strictement décroissante sur \(\mathbb{R}^-_0\). Elle n'a ni minimum, ni maximum.
- \(a=1/n\), \(n\in\mathbb{N}_0\). La fonction \(f(x)=x^{1/n}=\sqrt[n]x\) est une fonction racine. Lorsque \(n=2\), il s'agit de la fonction racine carrée définie sur \([0;+\infty[\) et dont la courbe représentative est la moitié supérieure de la parabole \(x=y^2\). Lorsque \(n\) est un autre nombre pair, le graphique de \(y=\sqrt[n]x\) est semblable à celui de \(y=\sqrt x\). A la valeur impaire \(n=3\) correspond la fonction racine cubique \(f(x)=\sqrt[3]x\) définie sur \(\mathbb{R}\). Le graphique de \(y=\sqrt[n]x\) pour \(n\) impair (\(n>3\)) ressemble à celui de \(y=\sqrt[3]x\).
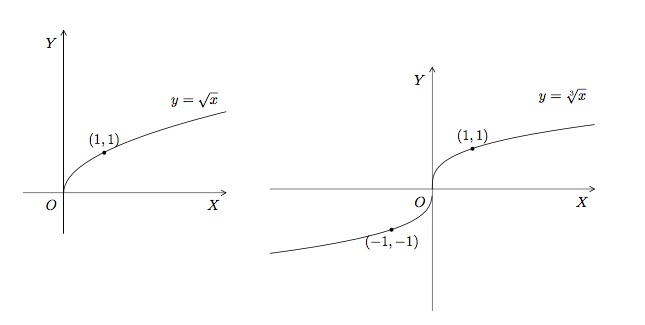
Pour \(n\) pair, la fonction \(\sqrt[n]{x}\) a une racine \(x=0\) et son ordonnée à l'origine est \(y=0\). Elle est toujours positive et nulle en \(0\). Elle n'est ni paire, ni impaire. Elle est strictement croissante sur \(\mathbb{R}^+\) et a un minimum en \(x=0\). Pour \(n\) impair, la fonction \(\sqrt[n]{x}\) a une racine \(x=0\) et son ordonnée à l'origine est \(y=0\). Elle est positive pour les valeurs de \(x\) positives et négative pour les valeurs de \(x\) négatives. Elle est impaire et strictement croissante sur \(\mathbb{R}\). Elle n'a ni minimum, ni maximum.
Cliquez sur le lien pour un rappel concernant les propriétés des racines.
(e) Fonctions polynomiales
Une fonction polynomiale est une fonction du type
\(P(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_2x^2+a_1x+a_0\)
où \(n\) est un entier positif et \(a_0, a_1, a_2,\ldots,a_n\) sont des constantes, appelées les coefficients du polynôme. Le domaine de définition de n'importe quel polynôme est \(\mathbb{R}\). L'indice \(n\) du premier coefficient \(a_n\) non nul donne le degré du polynôme.
Cliquez sur le lien pour plus de détails concernant les polynômes.
- \(n=1\). Une fonction polynomiale de degré 1 est de la forme \(P(x)=ax+b\) et est appelée une fonction affine. Son graphique est la droite \(y=ax+b\) de pente \(a\) et d'ordonnée à l'origine \(b\).
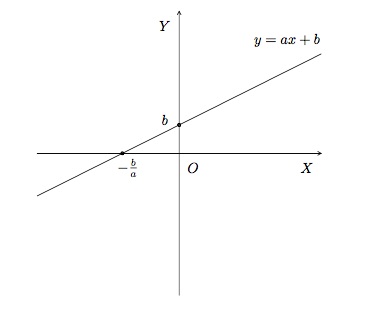
Elle possède une racine \(x=-\frac{b}{a}\) et son ordonnée à l'origine est \(y=b\). Elle est strictement croissante si \(a>0\) et strictement décroissante si \(a<0\).
Cliquez sur le lien pour un rappel sur les droites.
- Une fonction polynomiale de degré 2 est de la forme \(P(x)=ax^2+bx+c\) et est appelée une fonction quadratique. La courbe représentative de \(P\) est une parabole obtenue par déplacement de la parabole \(y=ax^2\). Voici la preuve de cette affirmation.
Cliquez sur le lien pour un rappel sur les paraboles.
(f) Fonctions rationnelles
Une fonction rationnelle \(f\) est un rapport de deux polynômes
\(f(x)=\dfrac{P(x)}{Q(x)}\)
où \(P\) et \(Q\) sont des polynômes. Le domaine de définition comprend toutes les valeurs de \(x\) qui n'annulent pas \(Q(x)\).
Par exemple, la fonction
\(f(x)=\dfrac{2x^4-x^2+1}{x^2-4}\)
est une fonction rationnelle dont le domaine de définition est \(\{x\ |\ x\neq\pm 2\}=\mathbb{R}\setminus\{-2,\, 2\}\).
(g) Fonctions trigonométriques
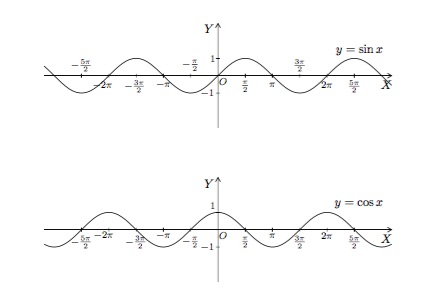
Tant pour la fonction sinus que pour la fonction cosinus, le domaine de définition est \(\mathbb{R}\) et l'ensemble image est l'intervalle fermé \([-1,1]\). En effet, quel que soit \(x\), on a
\(-1\le \sin x\le 1\mbox{ et } -1\le \cos x\le 1.\)
De plus, la fonction sinus s'annule pour chaque valeur de \(x\) égale à un multiple entier de \(\pi\). Autrement dit
\(\sin x=0 \quad\mbox{ quand }\quad x=k\pi \mbox{ avec } k \mbox{ entier}.\)
Une importante propriété des fonctions sinus et cosinus est leur caractère périodique, de période \(2\pi\). Cela signifie que, quel que soit \(x\),
\(\sin (x+2\pi)=\sin x\mbox{ et }\cos (x+2\pi)=\cos x.\)
Le caractère périodique de ces fonctions les rend particulièrement aptes à modéliser des phénomènes répétitifs comme les marées, les ressorts animés de vibrations ou les ondes sonores.
La fonction tangente est liée aux fonctions sinus et cosinus par l'équation
\(tg\, x=\dfrac{\sin x}{\cos x}.\)
Elle n'est pas définie lorsque \(\cos x=0\), c'est-à-dire lorsque \(x=\pm\pi/2, \pm 3\pi/2,\ldots\). Son ensemble image est \(\mathbb{R}\). Il est à noter que la fonction tangente est aussi périodique, mais de période \(\pi\) :
\(tg(x+\pi)=tg\, x.\)
Cliquez sur le lien pour des rappels concernant la trigonométrie.
Opérations sur les fonctions
(a) Opérations arithmétiques
Tout comme on associe deux nombres réels dans l'addition, la soustraction, la multiplication ou la division, on peut assembler deux fonctions \(f\) et \(g\) pour former de nouvelles fonctions, \(f+g\), \(f-g\), \(f\cdot g\) et \(f/g\).
Algèbre des fonctions - Soit \(f\) et \(g\) deux fonctions définies sur \(A\) et \(B\) respectivement. Alors, les fonctions \(f+g\), \(f-g\), \(fg\) et \(f/g\) sont définies comme suit :
\(\begin{array}{llll} (f+g)(x)&=&f(x)+g(x)\quad &\mbox{ domaine de définition} = A\cap B\\ (f-g)(x)&=&f(x)-g(x)\quad &\mbox{ domaine de définition} = A\cap B\\ (f\cdot g)(x)&=&f(x)\cdot g(x)\quad &\mbox{ domaine de définition} = A\cap B\\ \displaystyle \left(\frac fg\right)(x)&=&\displaystyle \frac{f(x)}{g(x)}\quad &\mbox{ domaine de définition} = \{x\in A\cap B | g(x)\ne 0\} \end{array}\)
Par exemple, la fonction somme \(f+g\) est définie par
\((f+g)(x)=f(x)+g(x).\)
Le membre de droite n'a du sens que si \(f(x)\) et \(g(x)\) sont définies, autrement dit, si \(x\) appartient à la fois au domaine de définition de \(f\) et de \(g\). Si le domaine de définition de \(f\) est \(A\) et celui de \(g\) est \(B\), alors le domaine de \(f+g\) est leur intersection \(A\cap B\). Le signe \(+\) du membre de gauche désigne une addition de fonctions tandis que le signe \(+\) du membre de droite désigne une simple addition entre les nombres réels \(f(x)\) et \(g(x)\).
Nous pouvons définir de la même manière la fonction différence \(f-g\) et la fonction produit \(f\cdot g\) et leur domaine de définition est aussi \(A\cap B\). Au moment de définir la fonction quotient \(f/g\), nous devons nous souvenir de ne pas diviser par 0.
On considère les fonctions \(f(x)=\sqrt x\) et \(g(x)=\sqrt{4-x^2}\). Le domaine de définition de \(f(x)=\sqrt x\) est \([0;+\infty[\). Le domaine de définition de \(g(x)=\sqrt{4-x^2}\) comprend toutes les valeurs de \(x\) telles que \(4-x^2\ge 0\), c'est-à-dire \(-2\le x\le 2\). Le domaine de définition de \(g\) est donc l'intervalle \([-2,2]\). L'intersection des domaines de définition de \(f\) et \(g\) est
\([0;+\infty[\,\cap\,[-2,+2]=[0,2].\)
De là, suivant les définitions, nous avons
\(\begin{array}{llll} (f+g)(x)&=&\sqrt x+\sqrt{4-x^2}\quad &\mbox{pour }0\le x\le 2\\ (f-g)(x)&=&\sqrt x-\sqrt{4-x^2}\quad &\mbox{pour }0\le x\le 2\\ (f\cdot g)(x)&=&\sqrt x\sqrt{4-x^2}=\sqrt{4x-x^3}\quad &\mbox{pour }0\le x\le 2\\ \displaystyle \left(\frac fg\right)(x)&=&\displaystyle \frac{\sqrt x}{\sqrt{4-x^2}}=\sqrt{\frac{x}{4-x^2}}\quad &\mbox{pour }0\le x<2 \end{array}\)
Vous aurez remarqué que le domaine de définition de \(f/g\) est l'intervalle \([0,2[\) car il a fallu exclure les valeurs de \(x\) en lesquelles \(g(x)=0\), à savoir \(x=\pm 2\).
Le graphique de la fonction \(f+g\) s'obtient par addition graphique. Cela signifie que, pour chaque valeur de \(x\), nous additionnons les ordonnées correspondantes.
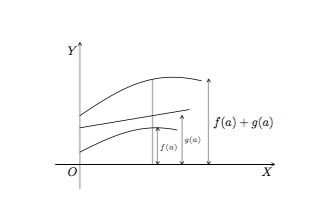
(b) Transformations de fonctions
En appliquant certaines transformations au graphique d'une fonction donnée, on obtient les graphiques de fonctions apparentées et on réduit ainsi fortement le travail nécessaire à la recherche de leur graphique.
Déplacements verticaux et horizontaux
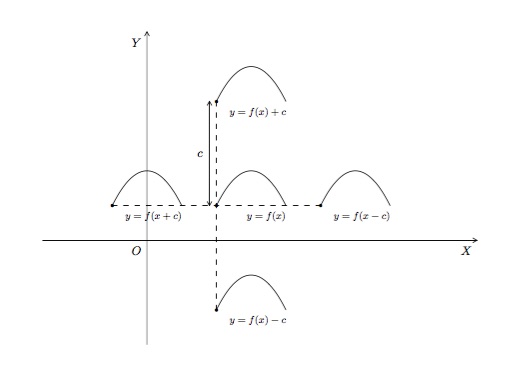
Considérons en premier lieu les translations. Si \(c\) est un nombre strictement positif, le graphique de \(y=f(x)+c\) est le même que celui de \(y=f(x)\) déplacé vers le haut de \(c\) unités (puisque chaque ordonnée \(y\) est augmentée de la même quantité \(c\)). De même, si \(g(x)=f(x-c)\) avec \(c>0\), la valeur de \(g\) en \(x\) est la même que la valeur de \(f\) en \(x-c\) (point situé \(c\) unités à gauche de \(x\)). De là, le graphique de \(g(x)=f(x-c)\) est le même que celui de \(y=f(x)\) déplacé de \(c\) unités vers la droite.
Déplacements verticaux et horizontaux - Supposons \(c>0\). Pour obtenir le graphique de
- \(y=f(x)+c\), déplacez le graphique de \(y=f(x)\) de \(c\) unités vers le haut
-
\(y=f(x)-c\), déplacez le graphique de \(y=f(x)\) de \(c\) unités vers le bas
-
\(y=f(x-c)\), déplacez le graphique de \(y=f(x)\) de \(c\) unités vers la droite
-
\(y=f(x+c)\), déplacez le graphique de \(y=f(x)\) de \(c\) unités vers la gauche
Etirements, compressions et réflexions
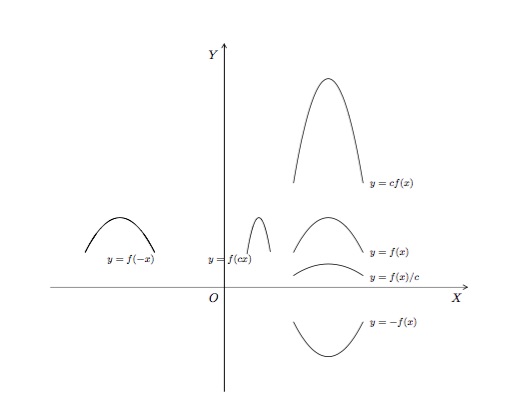
Si \(c>0\), alors le graphique de \(y=cf(x)\) est le graphique de \(y=f(x)\) étiré ou comprimé verticalement d'un facteur \(c\) (parce que chaque ordonnée \(y\) est multipliée par le même nombre \(c\)). Le graphique de \(y=-f(x)\) est le graphique de \(y=f(x)\) réfléchi par rapport à l'axe \(OX\) parce que le point \((x,y)\) est remplacé par le point \((x,-y)\).
Etirements et réflexions verticaux et horizontaux - Supposons \(c>1\). Pour obtenir le graphique de
-
\(y=cf(x)\), étirez verticalement le graphique de \(y=f(x)\) d'un facteur \(c\)
-
\(y=(1/c)f(x)\), comprimez verticalement le graphique de \(y=f(x)\) d'un facteur \(c\)
-
\(y=f(cx)\), comprimez horizontalement le graphique de \(y=f(x)\) d'un facteur \(c\)
-
\(y=f(x/c)\), étirez horizontalement le graphique de \(y=f(x)\) d'un facteur \(c\)
-
\(y=-f(x)\), prenez l'image symétrique du graphique de \(y=f(x)\) par rapport à l'axe \(OX\)
-
\(y=f(-x)\), prenez l'image symétrique du graphique de \(y=f(x)\) par rapport à l'axe \(OY\)
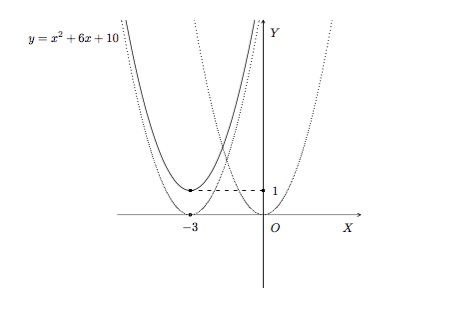
Dessinons la courbe représentative de la fonction \(f(x)=x^2+6x+10\). Le domaine de définition est \(\mathbb{R}\). En complétant le carré, nous écrivons l'équation de la courbe cherchée sous la forme
\(y=x^2+6x+10=(x+3)^2+1.\)
Dès lors, la courbe s'obtient en déplaçant la parabole \(y=x^2\) de 3 unités vers la gauche et de 1 unité vers le haut.
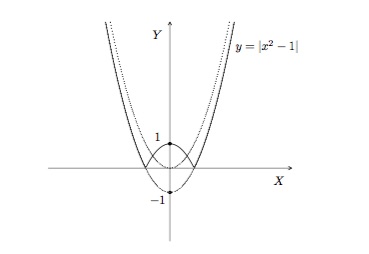
Dessinons la courbe représentative de \(y=|x^2-1|\). D'abord, nous traçons la parabole \(y=x^2-1\) en translatant d'une unité vers la bas la parabole \(y=x^2\). Nous pouvons voir qu'entre \(-1\) et \(1\) la courbe est sous l'axe \(OX\). Nous prenons l'image symétrique de cette partie par rapport à l'axe \(OX\) et laissons telle quelle le reste de la courbe. C'est le graphique de \(y=|x^2-1|\).
(c) Composition de fonctions
Une autre façon de créer de nouvelles fonctions est de les "composer'" entre elles. L'idée est d'appliquer des fonctions connues "en cascade", pour autant que les expressions ainsi obtenues aient toujours un sens.
Supposons, par exemple, que \(y=f(u)=\sqrt{u}\) et \(u=g(x)=x^2+1\). Comme \(y\) est une fonction de \(u\) et comme \(u\) est, à son tour, une fonction de \(x\), il s'ensuit que \(y\) est finalement une fonction de \(x\). Cette relation entre \(y\) et \(x\) se calcule par composition
\(y=f(u)=f(g(x))=f(x^2+1)=\sqrt{x^2+1}.\)
Cette opération s'appelle composition parce que la nouvelle fonction est composée des deux fonctions initiales \(f\) et \(g\).
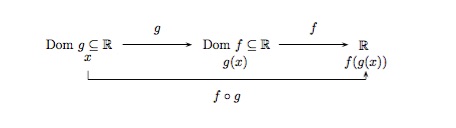
De façon générale, étant données deux fonctions \(f\) et \(g\), nous partons d'une valeur de \(x\) dans le domaine de définition de \(g\), nous calculons son image \(g(x)\). Si le nombre \(g(x)\) appartient au domaine de définition de \(f\), nous pouvons calculer la valeur \(f(g(x))\). Le résultat est une nouvelle fonction \(h(x)=f(g(x))\) obtenue en introduisant \(g\) dans \(f\). Elle s'appelle la "composée" de \(f\) et \(g\) et est notée \(f\circ g\) (\(f\) rond \(g\)).
\((f\circ g)(x)=f(g(x)).\)
Le domaine de définition de \(f\circ g\) est l'ensemble de toutes les valeurs de \(x\) du domaine de définition de \(g\) qui sont telles que \(g(x)\) appartient au domaine de définition de \(f\). Autrement dit, \(f\circ g\) est définie là où à la fois \(g(x)\) et \(f(g(x))\) sont définies. La meilleure image que l'on puisse donner de \(f\circ g\) est le diagramme suivant.
Si \(f(x)=x^2\) et \(g(x)=x-3\) alors on a
\((f\circ g)(x)=f(g(x))=f(x-3)=(x-3)^2,\)
\((g\circ f)(x)=g(f(x))=g(x^2)=x^2-3.\)
En général, \(f\circ g\ne g\circ f\). Souvenez-vous que la notation \(f\circ g\) signifie que la première fonction appliquée est \(g\) et la seconde \(f\). Ce qui, à l'exemple précédent, fait que pour appliquer \(f\circ g\), on soustrait d'abord 3, puis on élève au carré; alors que, pour appliquer \(g\circ f\), on devrait d'abord élever au carré, puis soustraire 3.
L'opération de composition s'applique aussi à trois fonctions ou davantage. Par exemple, la fonction composée \(f\circ g\circ h\) consiste à appliquer d'abord \(h\), ensuite \(g\) et finalement \(f\) :
\((f\circ g\circ h)(x)=f(g(h(x))).\)
Jusqu'à présent, par composition, nous avons construit des fonctions compliquées à partir de fonctions plus simples. Mais en analyse il est souvent utile ou nécessaire de décomposer une fonction compliquée en des fonctions plus simples.
Etant donnée la fonction \(F(x)=\cos^2(x+9)\), cherchons des fonctions \(f\), \(g\) et \(h\) telles que \(F=f\circ g\circ h\). La formule qui définit \(F\) dit : d'abord ajouter 9, puis prendre le cosinus du résultat, enfin, élever au carré. Ce qui fait que nous posons
\(h(x)=x+9,\quad g(x)=\cos x,\quad f(x)=x^2.\)
Effectivement
\(\begin{array} {lll}(f\circ g\circ h)(x)&=&f(g(h(x)))=f(g(x+9))=f(\cos(x+9))\\ &=&[\cos(x+9)]^2=F(x). \end{array}\)
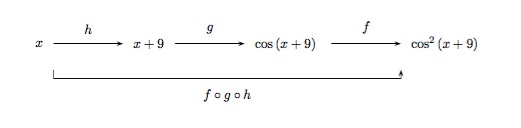
Exemples détaillés
- On considère la fonction \(f(x)=-2x+2\). Déterminer les racines et l'ordonnée à l'origine de cette fonction.
Solution détaillée : Les racines sont les solutions de l'équation \(f(x)=0\). On trouve \(-2x+2=0\) et donc \(x=1\). L'ordonnée à l'origine est la valeur \(f(0)\). On a \(f(0)=2\).
-
On considère la fonction \(f(x)=-2x+2\). Les couples \((0,0)\), \((1,0)\), \((3,1)\) et \((2,-2)\) appartiennent-ils au graphe de \(f\) ?
Solution détaillée : Les points \((1,0)\) et \((2,-2)\) appartiennent au graphe de \(f\). En effet, on a \(f(1)=-2+2=0\) et \(f(2)=-4+2=-2\). Les points \((0,0)\) et \((3,1)\) n'appartiennent pas au graphe de \(f\) car \(f(0)=2\neq 0\) et \(f(3)=-6+2=-4\neq 1\).
-
Pour la fonction \(f(x)=-2x+2\), calculer \(f(3)\), \(f(-1)\) et \(f(0)\).
Solution détaillée : En remplçant \(x\) par \(3\) dans la formule de la fonction, on obtient \(f(3)=-6+2=-4\). De même, on a \(f(-1)=2+2=4\) et \(f(0)=0+2=2\).
-
Déterminer les points d'abscisse \(2\) sur le graphe suivant.
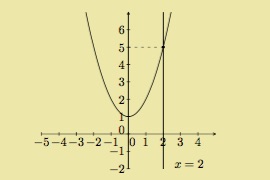
Solution détaillée : On trace la droite \(x=2\). Elle coupe le graphe en \(y=5\). Le point cherché est donc \((2,5)\).
-
Déterminer les points où \(f\) vaut \(2\).
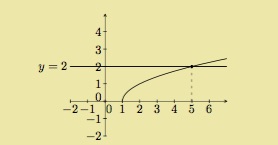
Solution détaillée : On trace la droite \(y=2\). Elle coupe le graphe en \(x=5\). Le point cherché est donc \((5,2)\).
-
Chercher le domaine de définition de la fonction \(g(x)=\frac{1}{x^2-x}\).
Solution détaillée : Etant donné que
\(g(x)=\frac{1}{x^2-x}=\frac{1}{x(x-1)},\)
et que la division par 0 n'est pas licite, nous constatons que \(g(x)\) n'est pas définie lorsque \(x=0\) ou \(x=1\). Dès lors, le domaine de définition de \(g\) est
\(\{x\, :\, x\ne 0, x\ne 1\}=\mathbb{R}\setminus\{0,1\}\)
qui, en termes d'intervalles, s'écrit aussi
\(]-\infty;0\,[\,\cup\,]\,0,1\,[\,\cup\,]\,1;+\infty[.\)
-
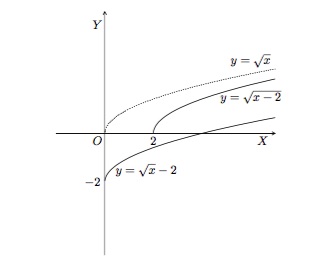
Etant donné la représentation graphique de \(y=\sqrt x\) (domaine \(\mathbb{R}^+\)), appliquer les transformations adéquates pour obtenir le graphique de \(y=\sqrt x-2\), \(y=\sqrt{x-2}\), \(y=-\sqrt x\), \(y=2\sqrt x\) et \(y=\sqrt{-x}\).
Solution détaillée : Nous traçons
- \(y=\sqrt x-2\) (domaine \(\mathbb{R}^+\)) en déplaçant la courbe \(y=\sqrt x\) de 2 unités vers le bas,
- \(y=\sqrt{x-2}\) (domaine \([2;+\infty[\)) en translatant la courbe \(y=\sqrt x\) de 2 unités vers la droite,
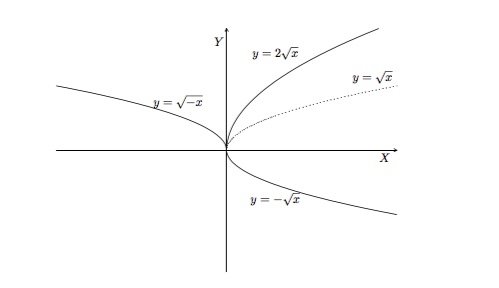
- \(y=-\sqrt x\) (domaine \(\mathbb{R}^+\)) en prenant l'image symétrique de la courbe \(y=\sqrt x\) par rapport à l'axe \(OX\),
- \(y=2\sqrt x\) (domaine \(\mathbb{R}^+\)) en étirant verticalement la courbe \(y=\sqrt x\) d'un facteur 2,
- \(y=\sqrt{-x}\) (domaine \(\mathbb{R}^-\)) en prenant l'image symétrique de la courbe \(y=\sqrt x\) par rapport à l'axe \(OY\).
-
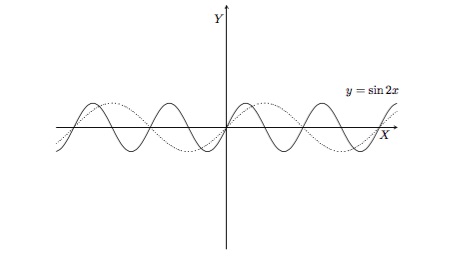
Faites le graphique de la fonction \(y=\sin 2x\).
Solution détaillée : Nous obtenons le graphique de \(y=\sin 2x\) en comprimant horizontalement d'un facteur 2 le graphique de \(y=\sin x\).
-
Faites le graphique de la fonction \(y=1-\sin x\).
Solution détaillée : Pour obtenir le graphique de \(y=1-\sin x\), nous prenons à nouveau celui de \(y=\sin x\) que nous réfléchissons autour de l'axe \(OX\) pour produire celui de \(y=-\sin x\) et ensuite nous le portons 1 unité plus haut.
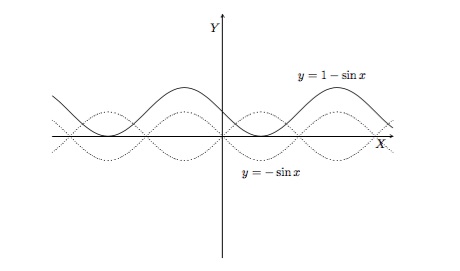
-
Si \(f(x)=\sqrt{2-x}\) et \(g(x)=\sqrt x\), définir \(f\circ g\) et son domaine de définition.
Solution détaillée : \((f\circ g)(x)=f(g(x))=f(\sqrt x)=\sqrt{2-\sqrt x}.\)
Pour que \(\sqrt x\) soit défini, il faut \(x\ge 0\). Pour que \(\sqrt{2-\sqrt x}\) soit défini, il faut \(2-\sqrt x\ge 0\), ce qui revient à \(\sqrt x\le 2\), ou encore à \(0\leq x\le 4\). Finalement, le domaine de définition de \(f\circ g\) est l'intervalle fermé \([0,4]\).
-
Un conteneur rectangulaire sans couvercle offre un volume de 10 m\(^3\). Un côté de sa base est deux fois plus long que l'autre. Le matériau pour la fabriquer revient à 10 euros le mètre carré tandis que celui des flancs revient à 6 euros le mètre carré. Exprimer le coût de fabrication en fonction du plus petit des côtés de la base.
Solution détaillée : Nous commençons par faire un croquis du conteneur en y indiquant les notations \(w\) et \(2w\) pour les côtés de la base et \(h\) pour la hauteur. Comme l'aire de la base mesure \((2w)w=2w^2\), son coût de fabrication est \(10(2w^2)\). Quant aux faces latérales, deux d'entre elles mesurent \(wh\) et les deux autres, \(2wh\). Leur coût, dans le matériau ad hoc, est donc \(6[2(wh)+2(2wh)]\). Le coût total s'élève à
\(C=10(2w^2)+6[2(wh)+2(2wh)]=20w^2+36wh.\)
Afin d'exprimer \(C\) comme fonction de la seule variable \(w\), nous devons éliminer \(h\) et pour cela nous utilisons le fait que le volume est de 10 m\(^3\). De
\(w(2w)h=10,\)
nous extrayons
\(h=\frac{10}{2w^2}=\frac{5}{w^2}.\)
Par substitution de cette expression de \(h\) dans celle de \(C\), nous obtenons
\(C=20w^2+36w\left(\frac{5}{w^2}\right)=20 w^2+\frac{180}{w}.\)
Finalement,
\(C(w)=20 w^2+\frac{180}{w},\qquad w>0\)
est l'expression de \(C\) en fonction de \(w\).
-
Trouver \(f\circ g\circ h\) pour \(f(x)=\frac{x}{x+1}\), \(g(x)=x^{10}\) et \(h(x)=x+3\).
Solution détaillée : Domaines de définition : les domaines de \(g\) et de \(h\) sont \(\mathbb{R}\); celui de \(f\) est \(\mathbb{R} \setminus \{-1\}\). Le domaine de définition de \(f\circ g\circ h\) est \(\{x \in \mbox{dom }h\) tels que \(h(x) \in \mbox{dom }g\) et tels que \(g(h(x)) \in \mbox{dom }f \}\), c'est-à-dire \(\{x \in \mathbb{R} \) tels que \((x+3)^{10}\not = -1 \}\). Comme \((x+3)^{10}\geq 0\) pour tout \(x\), le domaine de \(f\circ g\circ h\) est \(\mathbb{R}\) et
\(\begin{array} {ll}(f\circ g\circ h)(x)&=f(g(h(x)))=f(g(x+3))\\ &\displaystyle =f((x+3)^{10})= \frac{(x+3)^{10}}{(x+3)^{10}+1}. \end{array}\)
-
Décomposer la fonction \(F(x)=\sin^3{(x-4)}\) en trois fonctions \(f\), \(g\) et \(h\) telles que \(F=f\circ g\circ h\).
Solution détaillée : La formule qui définit \(F\) dit : d'abord retirer 4, puis prendre le sinus du résultat, enfin, élever au cube. Ce qui fait que nous posons
\(h(x)=x-4,\quad g(x)=\sin x,\quad f(x)=x^3.\)
Effectivement
\(\begin{array} {lll}(f\circ g\circ h)(x)&=&f(g(h(x)))=f(g(x-4))=f(\sin(x-4))\\ &=&[\sin(x-4)]^3=F(x). \end{array}\)