Théorie du module : Logarithmes et exponentielles

Le logarithme naturel

Les fonctions logarithmiques et exponentielles peuvent être définies de plusieurs manières. Ici, on part du logarithme naturel (également appelé logarithme népérien), que l'on définit à l'aide d'une primitive. On en déduit les propriétés de ce logarithme ainsi que les autres fonctions logarithmiques et les fonctions exponentielles.

(a) Définition

Nous cherchons une fonction \(f\) :

• dérivable,
• qui satisfait la condition \(f(xy)=f(x)+f(y)\).

Ces exigences imposent à la fonction que \(f(1)=0\) et qu'elle doit satisfaire à la propriété

\(f'(x)=\dfrac{c}{x},\)

pour \(x\neq 0\) et \(c=f'(1)\).  En effet,

\(f(1)=f(1\cdot 1)=f(1)+f(1)=2f(1)\)

Ceci n'est possible que si \(f(1)=0\).

Nous pouvons donc conclure que \(f(x)\) sera une primitive de \(\dfrac{c}{x}\). Nous choisissons \(c=1\) et tenons compte du fait que \(f(1)=0\). Cela nous mène à la définition suivante.

Le logarithme représente donc la surface sous la courbe de la fonction \(\dfrac{1}{t}\) de \(t=1\) à \(t=x\), comme on le voit sur la figure suivante

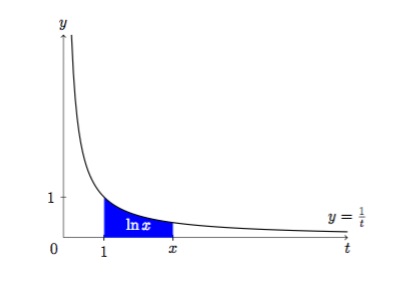
Figure 1 : La fonction \(\displaystyle\dfrac{1}{t}\) pour \(t>0\). La surface bleue donne la valeur de \(\ln x\).

 

Cette fonction est bien définie pour \(x>0\), car la fonction \(\displaystyle\dfrac{1}{t}\) est continue pour \(t>0\).

Le logarithme n'est par contre pas défini pour \(x<0\). En effet, l'intégrale \(\displaystyle\int_1^x\dfrac{1}{t}\, dt\) n'est pas bien définie pour \(x<0\) car l'intervalle \([x,1]\), sur lequel on intègre contient \(0\) et la fonction \(\displaystyle\dfrac{1}{t}\) n'est pas définie en \(0\), comme on peut le voir sur la Figure 2.

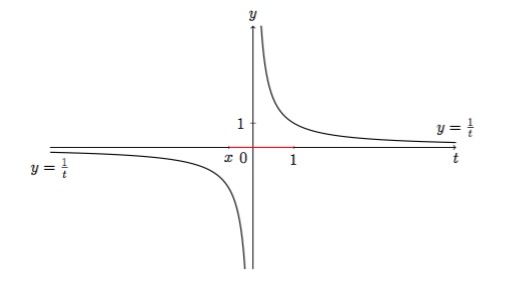
        Figure 2 : La fonction \(\displaystyle\dfrac{1}{t}\). L'intervalle en rouge est l'intervalle sur lequel on devrait intégrer cette fonction pour obtenir \(\ln x\) si \(x<0\).

 

(b) Propriétés

Voici des propriétés importantes du logarithme naturel.

Ces résultats sont une conséquence immédiate de la définition de \(\ln\). 

Les preuves de ces propriétés découlent de la définition : 

3. On a

\(\ln (xy)=\displaystyle\int_1^{xy}\dfrac{1}{t}\, dt=\underbrace{\displaystyle\int_1^x\dfrac{1}{t}\, dt}_{\ln x}+\displaystyle\int_x^{xy}\dfrac{1}{t}\, dt=\ln x+\displaystyle\int_x^{xy}\dfrac{\dfrac{1}{x}}{\dfrac{t}{x}}\, dt.\)

En effectuant la substitution \(s=\dfrac{t}{x}\), nous avons \(t\in[x,xy]\) d'où \(s=\dfrac{t}{x}\in[1,y]\) et donc
\(\ln(xy)=\ln x+\displaystyle\int_1^y\dfrac{1}{s}\, ds=\ln x+\ln y.\)

 

4. En utlisant la Propriété 3, on a pour \(p\in\mathbb{N}\) :

• Si \(p=0\), alors \(\ln x^0=\ln 1=0=0\cdot \ln x\).
• Si \(p\geq 1\), alors

\(\ln x^p=\ln(\underbrace{x\cdot x\cdots x}_{p\text{ facteurs}})=\underbrace{\ln x+\ln x+\cdots+\ln x}_{p\text{ termes}}=p\ln x.\)

Par exemple, on a

\(\ln 6=\ln(3\cdot 2)=\ln 3+\ln 2,\)

\(\ln 8=\ln 2^3=3\ln 2\)

\(\ln \sqrt{2}=\ln 2^{1/2}=\dfrac{1}{2}\ln 2 \)

 

5. La définition nous donne

\(\ln 1=\displaystyle\int_1^1\dfrac{1}{t}\, dt=0.\)

 

6. Ce résultat ainsi que la Propriété 3 nous permet de conclure que

\(\ln\dfrac{1}{x}+\ln x=\ln\left(\dfrac{1}{x}\cdot x\right)=\ln 1=0.\)

Nous avons donc que \(\displaystyle\ln\dfrac{1}{x}+\ln x=0\), ce qui est équivalent à \(\displaystyle\ln\dfrac{1}{x}=-\ln x\).

 

7. Pour \(x>1\), on a par la définition

\(\ln x=\displaystyle\int_1^x\dfrac{1}{t}\, dt.\)

Vu que nous intégrons une fonction positive et que la borne supérieure de l'intégrale (\(x\)) est plus grande que la borne inférieure (1), l'intégrale sera donc positive.

Si \(x<1\), on a que \(\dfrac{1}{x}>1\). La Propriété 6 nous permet de conclure que

\(\ln x=-\underbrace{\ln\dfrac{1}{x}}_{>0}<0.\)

Par exemple, on a

\(\ln 2 >0,\mbox{ mais }\displaystyle\ln\dfrac{1}{2}=-\ln 2<0.\)

 

 

(c) Représentation graphique de ln x

Nous allons maintenant analyser le comportement de la fonction \(\ln\). Nous savons déjà plusieurs choses utiles pour cette analyse :

• le domaine de \(\ln\) est \(\mathbb R^+_0\),
• la dérivée: \(\displaystyle(\ln x)'=\dfrac{1}{x}\),
• des valeurs particulières : \(\ln 1=0\) et \(\ln e=1\),
• le signe : \(\ln x<0\) si \(0<x<1\), et \(\ln x>0\) si \(x>1\).

Voici quelques propriétés supplémentaires.

Si vous êtes intéressé, vous pouvez regarder la preuve de ces propriétés.

La fonction \(\ln{x}\) étant strictement croissante et concave sur tout son domaine, elle n'a ni extremum, ni point d'inflexion.

Résumons ce que nous savons de cette fonction dans un tableau :

 

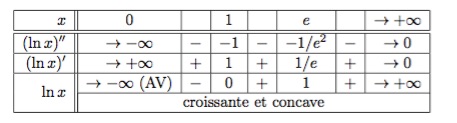
Ceci nous permet d'obtenir le graphique suivant :

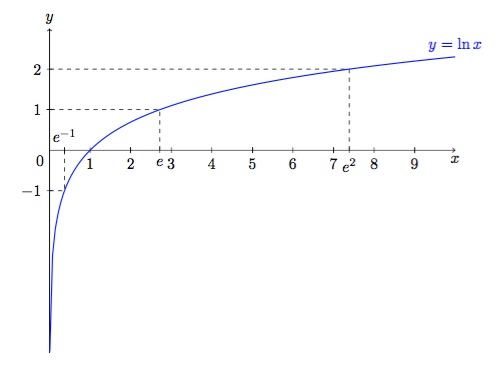
Figure 3 : Graphique de \(\ln x \).

 

Le logarithme en base a

(a) Définition

Nous voudrions étendre le logarithme naturel, vers des fonctions qui satisfont \(f(a)=1\) pour des valeurs de \(a\) différentes de \(e \). Ces fonctions doivent toujours être dérivables et doivent toujours satisfaire à la condition \(f(xy)=f(x)+f(y) \). Nous allons définir ces fonctions à l'aide du logarithme naturel.

Par exemple, on a

\(\log_ex=\dfrac{\ln x}{\ln e}=\ln x\)

et

\(\log_{10}x=\dfrac{\ln x}{\ln 10}.\)

On ne note généralement pas la base \(10 \), on écrit donc \( \log x \) pour \(\log_{10}x \).

Un autre logarithme qui revient régulièrement est le logarithme en base \(2 \) :

\(\log_2x=\dfrac{\ln x}{\ln 2}.\)

 

(b) Propriétés

Voici des propriétés importantes du logarithme en base \(a\).

Ces propriétés montrent que la fonction \(\log_a\) satisfait les conditions requises.  Les preuves de ces propriétés découlent de la définition :

1. La fonction \(\log_a x\) est dérivable, vu que \(\ln x\) est dérivable, et la dérivée est donnée par

   \((\log_a x)'=\left(\dfrac{\ln x}{\ln a}\right)'=\dfrac{1}{\ln a}(\ln x)'=\dfrac{1}{\ln a}\cdot\dfrac{1}{x}=\dfrac{1}{x\ln a}.\)

 

 

 

2. On a

   \(\log_a a=\dfrac{\ln a}{\ln a}=1.\)

3. Nous avons également que

   \(\log_a 1=\dfrac{\ln 1}{\ln a}=\dfrac{0}{\ln a}=0.\)

 

4. On déduit des propriétés de \(\ln\) que

   \(\log_a(xy)=\dfrac{\ln(xy)}{\ln a}=\dfrac{\ln x+\ln y}{\ln a}=\dfrac{\ln x}{\ln a}+\dfrac{\ln y}{\ln a}=\log_a x+\log_a y.\)

 

5. Ce résultat s'explique par le résultat obtenu pour la fonction \(\ln \). En effet,

   \(\log_a x^p=\dfrac{\ln x^p}{\ln a}=\dfrac{p\ln x}{\ln a}=p\dfrac{\ln x}{\ln a}=p\log_a x.\)

Par exemple, on a

\(\log_2 8=\log_2 2^3=3\log_2 2=3.\)

 

6. En utilisant les Propriétés 3 et 4, on a

   \(\log_a x+\log_a\dfrac{1}{x}=\log_a\left(x\cdot\dfrac{1}{x}\right)=\log_a 1=0.\)

 

7. De même, en utilisant la Propriété 6 de la fonction \(\ln{x} \), on a

   \(\log_{1/a} x=\dfrac{\ln x}{\ln\dfrac{1}{a}}=\dfrac{\ln x}{-\ln a}=-\dfrac{\ln x}{\ln a}=-\log_a x.\)

Par exemple,

\(\log_{1/2}8=-\log_28=-\log_22^3=-3.\)

 

8. Si \(a>1 \) alors pour tout \(x>0 \), on a

\(\log_a x=\dfrac{\ln x}{\ln a},\quad\text{avec } \ln a>0.\)

La fonction \(\log_a x\) a donc le même signe que \(\ln x \), c'est-à-dire \(\log_a x>0\) si \(x>1\) et \(\log_a x<0 \) si \(0<x<1 \).

 

9. Par contre, si \(0<a<1\) alors \(\dfrac{1}{a}>1\) et pour tout \(x>0 \), on a

   \(\log_a x=\dfrac{\ln x}{\ln a}=\dfrac{\ln x}{-\ln\dfrac{1}{a}}=-\dfrac{\ln x}{\ln\dfrac{1}{a}},\quad\text{avec } \ln\dfrac{1}{a}>0.\)

   Le signe de \(\log_a x\) est donc dans ce cas opposé à celui de \(\ln x \), c'est-à-dire \(\log_a x<0\) si \(x>1\) et \(\log_a x>0\) si \(0<x<1 \).

Nous avons \(\log_28=3>0\) (puisque \(a=2>1\) et \(x=8>1 \)) et \(\log_{1/2}8=-3<0\) (puisque \(0<a=1/2<1\) et \(x=8>1 \)). Nous avons également

\(\log_2\dfrac{1}{8}=\log_2 2^{-3}=-3\log_22=-3<0,\)

puisque \(a=2>1\) et \(0<x=\dfrac{1}{8}<1 \), alors que

\(\log_{1/2}\dfrac{1}{8}=\log_{1/2}\left(\dfrac{1}{2}\right)^3=3\log_{1/2}\dfrac{1}{2}=3>0,\)

puisque \(0<a=\dfrac{1}{2}<1\) et \(0<x=\dfrac{1}{8}<1 \).

 

(c) Représentation graphique de la fonction logarithme en base a

Nous allons maintenant analyser le comportement de la fonction \(\log_a \), où \(a>0\) et \(a\neq 1 \). Nous savons déjà plusieurs choses utiles pour cette analyse :

• le domaine de \(\log_a \) est \(\mathbb R^+_0 \),
• la dérivée : \(\displaystyle(\log_a x)'=\dfrac{1}{x\ln a} \),
• des valeurs particulières : \(\log_a 1=0\) et \(\log_a a=1 \),
• le signe de \(\log_ax \) dépend non seulement de \(a \), mais également de \(x \).

Le comportement de \(\log_a \) est dépendant de la valeur de \(a \). On a déjà vu qu'il y avait des différences de signe selon que \(a>1\) ou que \(0<a<1 \).

Nous allons étudier séparément les cas \(a>1\) et \(0<a<1 \) afin de voir si la fonction est croissante, décroissante, convexe ou concave.

Si vous êtes intéressé, vous pouvez regarder la preuve de ces propriétés.

La fonction \(\log_a x\) étant strictement croissante et concave sur tout son domaine pour \(a>1\), elle n'a ni extremum, ni point d'inflexion.

La fonction \(\log_a x\) étant strictement décroissante et convexe sur tout son domaine pour \(0<a<1 \), elle n'a ni extremum, ni point d'inflexion.

Résumons ce que nous savons de ces fonctions dans un tableau :

• \(a>1\)

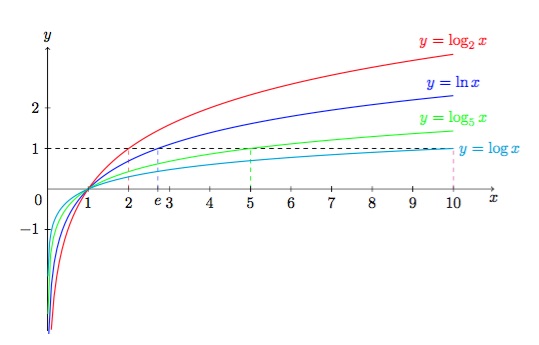
Figure 4 : Graphique de \(\log_2 x \), de \(\ln x \), de \(\log_5 x\) et de \(\log x=\log_{10} x \).

 

• \(0<a<1\)

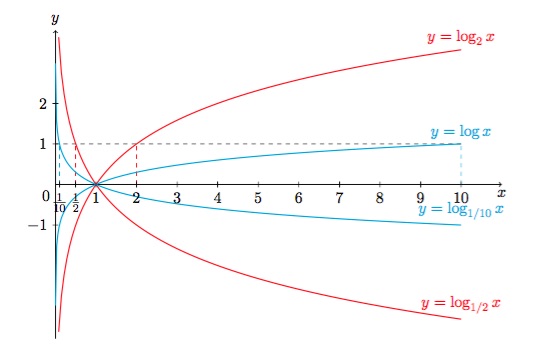
Figure 5 : Graphique de \(\log_{1/10} x \), de \(\log_{1/2} x \), de \(\log_2 x \) et de \(\log x \).

Fonctions exponentielles

(a) Définition

Nous avons vu que la fonction

\(\ln:\mathbb R^+_0\to\mathbb R:x\mapsto\ln x\)

est une bijection. Ceci implique que pour tout \(a>0\) et \(a\neq 1 \), la fonction

\(\log_a:\mathbb R^+_0\to\mathbb R:x\mapsto\log_ax=\dfrac{\ln x}{\ln a}\)

est également une bijection. La fonction \(\log_a\) a donc une fonction réciproque que nous appellerons fonction exponentielle en base a .

Nous avons donc

\(\forall y\in\mathbb R^+_0:\,\exp_a(\log_a y)=y\)

et

\(\forall x\in\mathbb R:\,\log_a(\exp_a x)=x.\)

Comme nous avons vu dans la Propriété 5 de la fonction \(\log_a{x}\) que pour tout \(x\in\mathbb Q \),

\(\log_a a^x=x\log_a a=x,\)

on peut en conclure que pour tout \(x\in\mathbb Q \),

\(\exp_a x=a^x.\)

Cela parait naturel de ne pas se restreindre aux nombres rationnels, mais d'étendre à tous les nombres réels. Ceci nous permet de définir des puissances à exposant réel.

 (b) Le cas particulier de l'exponentielle en base e

Nous avons vu que \(\ln x=\log_e x \), où \(e\) est un nombre irrationnel et \(e=2.71828\dots \).

La réciproque de \(\ln x\) est donc \(e^x \).

Puisque la fonction \(e^x \) est la réciproque de \(\ln x\) nous savons que

\(f(x)=e^x\iff x=\ln{(f(x))}.\)

1. Dérivons le membre de gauche et de droite de \(x=\ln{(f(x))}\) : la dérivée du membre de gauche est \((x)'=1 \)et la dérivée du membre de droite est \(\left(\ln{(f(x))}\right)'=f'(x)\ln'{(f(x))}=\dfrac{f'(x)}{f(x)} \).

   En rassemblant les deux, on peut conclure que \(1=\dfrac{f'(x)}{f(x)}\).

   On peut réécrire cette égalité comme

   \(f(x)=f'(x),\)

   et donc

   \((e^x)'=f'(x)=f(x)=e^x.\)

 

2. Le calcul la dérivée de \(e^x+C\) nous donne

   \(\left(e^x+C\right)'=e^x+0=e^x.\)

   Les fonctions de la forme \(e^x+C\) sont donc bien des primitives de \(e^x \). Il n'y en a pas d'autres, car les primitives ne diffèrent que d'une constante.

(c) Propriétés de la fonction exponentielle en base a

Voici des propriétés importantes des fonctions exponentielles en base \(a \).

En effet,

1. on a \(\log_a e^{x\ln a}=\dfrac{\ln e^{x\ln a}}{\ln a}=\dfrac{x\ln a}{\ln a}=x.\) Sachant que \(x=\log_a y\) si et seulement si \(y=a^x \), on en déduit \(e^{x\ln a}=a^x \).

 

2. nous savons que \(a^x=e^{x\ln a} \) et \(\left(e^x\right)'=e^x \). En utilisant la formule de dérivation des fonctions composées, on obtient

   \(\left(a^x\right)'=\left(e^{x\ln a}\right)'=(x\ln a)'e^{x\ln a}=\ln a\cdot e^{x\ln a}=\ln a\cdot a^x=a^x\ln a.\)

 

3. on a \(x=\log_a a^x \).  Sachant que \(\log_a\dfrac{1}{a}=-1 \), on obtient

\(\log_a\left(\dfrac{1}{a}\right)^x=x\log_a\dfrac{1}{a}=x\cdot (-1)=-x=\log_aa^{-x}.\)

 

Ceci permet de conclure que

\(\left(\dfrac{1}{a}\right)^x=a^{-x}.\)

 

4. nous savons aussi que \(x+y=\log_a a^{x+y} \) et donc

   \(\log_a a^{x+y}=x+y=\log_a a^x+\log_a a^y=\log_a\left(a^x\cdot a^y)\right.\)

   On peut donc conclure que

   \(a^{x+y}=a^x\cdot a^y.\)

 

5. Finalement l'utilisation de \(\log_ax^p=p\log_ax\) nous permet d'obtenir

   \(\log_a\left(a^x\right)^y=y\log_a a^x=yx=xy=\log_a a^{xy}.\)

   On en conclut que

   \(\left(a^x\right)^y=a^{xy}.\)

    

(d) Représentation graphique de la fonction exponentielle en base a

Nous allons maintenant analyser le comportement de la fonction \(a^x \), où \(a>0\) et \(a\neq 1 \). Nous savons déjà plusieurs choses utiles pour cette analyse :

• le domaine de la fonction \(a^x \) est \(\mathbb R \),

• la dérivée : \(\left(a^x\right)'=a^x\ln a \),

• des valeurs particulières : \(a^0=1\) et \(a^1=a \).

Comme pour la fonction \(\log_a \), nous allons traiter séparément les cas \(a>1\) et \(0<a<1 \). 

Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.

Résumons ce que nous savons de ces fonctions dans un tableau : 

• \(a>1\)

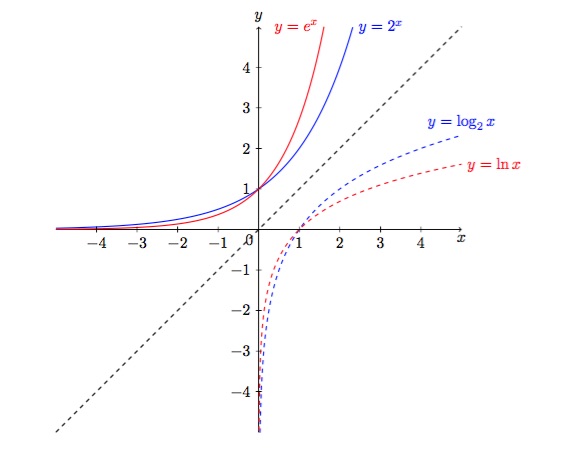
Figure 6 : Graphique de \(2^x \), \(e^x \), \( \log_2 x\) et de \(\ln x \).

 

Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.

Résumons ce que nous savons de ces fonctions dans un tableau : 

• \(0<a<1\)

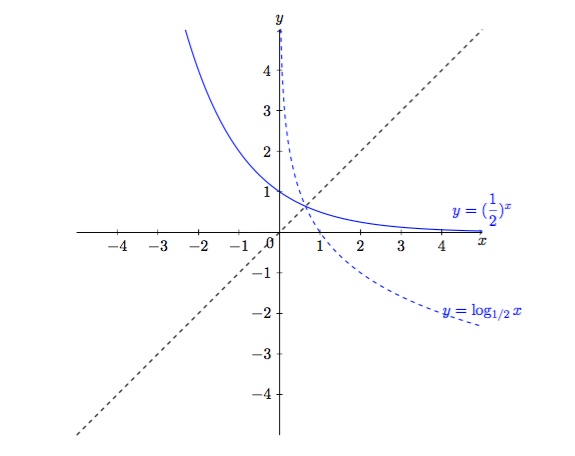
Figure 7 : Graphique de \(\displaystyle \left(\dfrac{1}{2}\right)^x\) et de \(\log_{1/2} x \).

 

Le graphique de \(a^x\) est l'image de celui de \(\log_ax\) par la symétrie orthogonale par rapport à la droite \(y=x\) (la première bissectrice).

Exemples détaillés

1. Sachant que \(\ln 2=0,693 \), \(\ln 3=1,099 \), \(\ln 5=1,609 \), calculer \(\ln 90 \).

Solution détaillée : On a

\(\begin{array}{rcl} \ln 90&=&\ln\left(3^2\cdot2\cdot 5\right)=\ln 3^2+\ln 2+\ln5\\ &=&2\ln 3+\ln 2+\ln 5\\ &=&2\cdot 1,099+0,693+1,609=4,5 \end{array}\)

 

2. Transformer de manière à ce qu'il ne reste plus de logarithme dans l'expression \(\log_8\sqrt{2} \).

Solution détaillée : En utilisant les propriétés des logarithmes, on a

\(\log_8\sqrt{2}=\log_82^{1/2}=\dfrac{1}{2}\log_82=\dfrac{1}{2}\log_8(8)^{1/3}=\dfrac{1}{2}\cdot\dfrac{1}{3}\log_88=\dfrac{1}{2}\cdot\dfrac{1}{3}\cdot 1=\dfrac{1}{6}.\)

 

3. Déterminer le domaine et la dérivée de la fonction \(f(x)=\ln{(\sin x)} \).

Solution détaillée : La fonction \(\ln x\) n'est définie que pour \(x>0 \). La fonction \(\ln(\sin x)\) n'est donc définie que pour\( \sin x>0 \). Or

\(\sin x=0\iff x=k\pi,\quad\forall k\in\mathbb Z.\)

Nous avons que

\(\sin x>0\text{ si } 0<x<\pi\quad\text{et}\quad \sin x<0\text{ si }\pi<x<2\pi.\)

La fonction \(\sin x\) étant \(2\pi \)-périodique : \(\sin x>0 \iff 2k\pi<x<(2k+1)\pi , \forall k\in\mathbb Z \). Le domaine est donc

\(\displaystyle\bigcup_{k\in\mathbb Z}]2k\pi;(2k+1)\pi[\, .\)

On calcule en utilisant la formule de dérivation des fonctions composées

\(\left(\ln(\sin x)\right)'=(\sin x)'\ln'(\sin x)=\cos x\cdot \dfrac{1}{\sin x}=\dfrac{\cos x}{\sin x}=cotg\, x.\)

 

4. Déterminer le domaine et la dérivée de la fonction \(f(x)=xe^{1/x} \).

Solution détaillée : Les fonctions \(e^x\) et \(x\) ont \(\mathbb R\) comme domaine, ce qui implique que \(xe^{1/x}\) a le même domaine que \(\displaystyle\dfrac{1}{x} \). Le domaine de \(\displaystyle\dfrac{1}{x} \) est \(\mathbb R_0 \), qui est donc également le domaine de \(xe^{1/x}\).

En utilisant la règle de dérivation d'un produit, on calcule

\(\begin{array}{rcl} (xe^{1/x})'&=&(x)'e^{1/x}+x(e^{1/x})'\\[2mm] &=&1\cdot e^{1/x}+x\left(\dfrac{1}{x}\right)'e^{1/x}\\[2mm] &=&e^{1/x}+x\cdot \dfrac{-1}{x^2}\cdot e^{1/x}\\[2mm] &=&e^{1/x}-\dfrac{1}{x}\cdot e^{1/x}=\left(1-\dfrac{1}{x}\right)e^{1/x} \end{array}\)

 

5. Calculer la limite \( \displaystyle\lim_{x\to 1} \left(\ln(1-x^4)-\ln(1-x^2)\right)\).

Solution détaillée : On a

\(\begin{array}{rcl} \displaystyle\lim_{x\to 1} \left(\ln(1-x^4)-\ln(1-x^2)\right)&=&\displaystyle\lim_{x\to 1}\ln\dfrac{1-x^4}{1-x^2}\\ &=&\displaystyle\lim_{x\to 1}\ln\dfrac{(1-x^2)(1+x^2)}{1-x^2}\\ &=&\lim_{x\to 1}\ln(1+x^2)=\ln 2. \end{array}\)

 

6. Calculer la limite \(\displaystyle\lim_{x\to +\infty} \ln\left(\ln\left(e+\dfrac{1}{x}\right)\right) \).

Solution détaillée : On calcule

\(\displaystyle\lim_{x\to+\infty}\ln\left(e+\dfrac{1}{x}\right)=1\)

et donc puisque la fonction \(\ln x\) est continue,

\(\displaystyle\lim_{x\to +\infty} \ln\left(\ln\left(e+\dfrac{1}{x}\right)\right)=\ln(1)=0.\)

 

7. Résoudre l'équation \(\ln (x-5)+\ln (x-2)=2\ln 2 \).

 Solution détaillée : Les solution de cette équation doivent être dans le domaine de \(\ln (x-5)\) et de \(\ln(x-2) \).  Il faut donc que \(x-5>0\) et \(x-2>0 \), ce qui implique \(x>5 \). On a

\(\ln(x-5)+\ln(x-2)=2\ln 2\)

\(\ln\left[(x-5)(x-2)\right]=2\ln 2\)

\(\ln\left[(x-5)(x-2)\right]=\ln 2^2\)

\(\ln\left(x^2-7x+10\right)=\ln 4\)

Si \(x\) satisfait à \(\ln\left(x^2-7x+10\right)=\ln 4 \), \(x\) satisfait également à \(x^2-7x+10=4.\)

Toutes les solutions de cette dernière équation ne sont pas nécessairement des solutions de notre problème de départ, il faut également que \(x>5 \).

Résolvons l'équation \(x^2-7x+10=4\). Cette équation est équivalente à l'équation \(x^2-7x+6=0\). On calcule

\(x=\dfrac{7+\sqrt{25}}{2}=\dfrac{7+5}{2}=6\quad\mbox{ ou }\quad x=\dfrac{7-5}{2}=1.\)

La seule solution valable est donc \(x=6 \), car l'autre solution ne satisfait pas à \(x>5 \).

 

8. Résoudre l'équation \(2^{6x}-3\cdot2^{3x}-4=0 \).

Solution détaillée : On a

\(2^{6x}-3\cdot2^{3x}-4=0\)

\(\left(2^{3x}\right)^2-3\cdot2^{3x}-4=0\)

Posons \(y=2^{3x}\) et nous obtenons l'équation quadratique \(y^2-3y-4=0.\)  Les solutions sont

\(y=\dfrac{3+5}{2}=4\quad\mbox{ ou }\quad y=\dfrac{3-5}{2}=-1.\)

Il faut que \(y=2^{3x}>0 \), il est donc impossible que \(y=-1 \). La seule solution valable est donc \(y=4 \). Ceci implique que

\(2^{3x}=4\)

\(\log_22^{3x}=\log_2 4\)

\(3x=\log_24\)

\(3x=\log_2(2)^2\)

\(3x=2\log_22\)

\(x=\dfrac{2}{3}\)

 

Preuves