Auto-Math

Université catholique de Louvain - UCL

Théorie du module : Logarithmes et exponentielles

Le logarithme en base a

(a) Définition

Nous voudrions étendre le logarithme naturel, vers des fonctions qui satisfont \(f(a)=1\) pour des valeurs de \(a\) différentes de \(e \). Ces fonctions doivent toujours être dérivables et doivent toujours satisfaire à la condition \(f(xy)=f(x)+f(y) \). Nous allons définir ces fonctions à l'aide du logarithme naturel.

Définition - Soit \(a>0\) et \(a\neq 1 \). Le logarithme en base a, noté \(\log_a \), est donné par

\(\log_a:\mathbb R^+_0\to\mathbb R:x\mapsto\log_ax=\dfrac{\ln x}{\ln a}.\)

Par exemple, on a

\(\log_ex=\dfrac{\ln x}{\ln e}=\ln x\)

et

\(\log_{10}x=\dfrac{\ln x}{\ln 10}.\)

On ne note généralement pas la base \(10 \), on écrit donc \( \log x \) pour \(\log_{10}x \).

Un autre logarithme qui revient régulièrement est le logarithme en base \(2 \) :

\(\log_2x=\dfrac{\ln x}{\ln 2}.\)

 

(b) Propriétés

Voici des propriétés importantes du logarithme en base \(a\).

Propriétés : Soit \(a>0\),  \(a\neq 1\), \(x,y>0 \) et \(p\in\mathbb Q\).  On a

  1. La fonction \(\log_a x \) est dérivable et sa dérivée est donnée par \((\log_a{x})'=\dfrac{1}{x\ln a}.\)
  2. \(\log_a a=1 \)
  3. \(\log_a 1=0 \)
  4. \( \log_a (xy)=\log_a x+\log_a y \)
  5. \(\log_a x^p=p\log_a x \)
  6. \(\log_a\dfrac{1}{x}=-\log_a x \)
  7. \(\log_{1/a}x=-\log_a x \)

  8. Si \(a>1 \), alors pour tout \(x>0 \), on a

  • si \(x>1\) alors \(\log_a x>0\)

  • si \(0<x<1\) alors \(\log_a x<0\)

  1.  Si \(0<a<1 \), alors pour tout \(x>0 \), on a
  • si \(x>1\) alors \(\log_a x<0\)
  • si \(0<x<1\) alors \(\log_a x>0\) 

Ces propriétés montrent que la fonction \(\log_a\) satisfait les conditions requises.  Les preuves de ces propriétés découlent de la définition :

  1. La fonction \(\log_a x\) est dérivable, vu que \(\ln x\) est dérivable, et la dérivée est donnée par

    \((\log_a x)'=\left(\dfrac{\ln x}{\ln a}\right)'=\dfrac{1}{\ln a}(\ln x)'=\dfrac{1}{\ln a}\cdot\dfrac{1}{x}=\dfrac{1}{x\ln a}.\)

 

 

 

  1. On a

    \(\log_a a=\dfrac{\ln a}{\ln a}=1.\)

  2. Nous avons également que

    \(\log_a 1=\dfrac{\ln 1}{\ln a}=\dfrac{0}{\ln a}=0.\)

 

  1. On déduit des propriétés de \(\ln\) que

    \(\log_a(xy)=\dfrac{\ln(xy)}{\ln a}=\dfrac{\ln x+\ln y}{\ln a}=\dfrac{\ln x}{\ln a}+\dfrac{\ln y}{\ln a}=\log_a x+\log_a y.\)

 

  1. Ce résultat s'explique par le résultat obtenu pour la fonction \(\ln \). En effet,

    \(\log_a x^p=\dfrac{\ln x^p}{\ln a}=\dfrac{p\ln x}{\ln a}=p\dfrac{\ln x}{\ln a}=p\log_a x.\)

Par exemple, on a

\(\log_2 8=\log_2 2^3=3\log_2 2=3.\)

 

  1. En utilisant les Propriétés 3 et 4, on a

    \(\log_a x+\log_a\dfrac{1}{x}=\log_a\left(x\cdot\dfrac{1}{x}\right)=\log_a 1=0.\)

 

  1. De même, en utilisant la Propriété 6 de la fonction \(\ln{x} \), on a

    \(\log_{1/a} x=\dfrac{\ln x}{\ln\dfrac{1}{a}}=\dfrac{\ln x}{-\ln a}=-\dfrac{\ln x}{\ln a}=-\log_a x.\)

Par exemple,

\(\log_{1/2}8=-\log_28=-\log_22^3=-3.\)

 

  1. Si \(a>1 \) alors pour tout \(x>0 \), on a

\(\log_a x=\dfrac{\ln x}{\ln a},\quad\text{avec } \ln a>0.\)

La fonction \(\log_a x\) a donc le même signe que \(\ln x \), c'est-à-dire \(\log_a x>0\) si \(x>1\) et \(\log_a x<0 \) si \(0<x<1 \).

 

  1. Par contre, si \(0<a<1\) alors \(\dfrac{1}{a}>1\) et pour tout \(x>0 \), on a

    \(\log_a x=\dfrac{\ln x}{\ln a}=\dfrac{\ln x}{-\ln\dfrac{1}{a}}=-\dfrac{\ln x}{\ln\dfrac{1}{a}},\quad\text{avec } \ln\dfrac{1}{a}>0.\)

    Le signe de \(\log_a x\) est donc dans ce cas opposé à celui de \(\ln x \), c'est-à-dire \(\log_a x<0\) si \(x>1\) et \(\log_a x>0\) si \(0<x<1 \).

Nous avons \(\log_28=3>0\) (puisque \(a=2>1\) et \(x=8>1 \)) et \(\log_{1/2}8=-3<0\) (puisque \(0<a=1/2<1\) et \(x=8>1 \)). Nous avons également

\(\log_2\dfrac{1}{8}=\log_2 2^{-3}=-3\log_22=-3<0,\)

puisque \(a=2>1\) et \(0<x=\dfrac{1}{8}<1 \), alors que

\(\log_{1/2}\dfrac{1}{8}=\log_{1/2}\left(\dfrac{1}{2}\right)^3=3\log_{1/2}\dfrac{1}{2}=3>0,\)

puisque \(0<a=\dfrac{1}{2}<1\) et \(0<x=\dfrac{1}{8}<1 \).

 

(c) Représentation graphique de la fonction logarithme en base a

Nous allons maintenant analyser le comportement de la fonction \(\log_a \), où \(a>0\) et \(a\neq 1 \). Nous savons déjà plusieurs choses utiles pour cette analyse :

  • le domaine de \(\log_a \) est \(\mathbb R^+_0 \),
  • la dérivée : \(\displaystyle(\log_a x)'=\dfrac{1}{x\ln a} \),
  • des valeurs particulières : \(\log_a 1=0\) et \(\log_a a=1 \),
  • le signe de \(\log_ax \) dépend non seulement de \(a \), mais également de \(x \).

Le comportement de \(\log_a \) est dépendant de la valeur de \(a \). On a déjà vu qu'il y avait des différences de signe selon que \(a>1\) ou que \(0<a<1 \).

Nous allons étudier séparément les cas \(a>1\) et \(0<a<1 \) afin de voir si la fonction est croissante, décroissante, convexe ou concave.

Propriétés : Soit \(a>0\) et \(a\neq 1 \).

  1. Si \(a>1\), la fonction \(\log_a x\) est strictement croissante sur tout son domaine.

  2. Si \(0<a<1 \), la fonction \(\log_a x\) est strictement décroissante sur tout son domaine.

  3. Si \(a>1\), la fonction \(\log_a x\) est concave sur tout son domaine.

  4. Si \(0<a<1 \), la fonction \(\log_a x\) est convexe sur tout son domaine.

  5. Le graphique de \(\log_a x\) a comme asymptote verticale \(x=0 \).

  6. Le graphique de \(\log_a x\) n'a pas d'asymptote horizontale.

  7. Le graphique de \(\log_a x\) n'a pas d'asymptote oblique.

Si vous êtes intéressé, vous pouvez regarder la preuve de ces propriétés.

La fonction \(\log_a x\) étant strictement croissante et concave sur tout son domaine pour \(a>1\), elle n'a ni extremum, ni point d'inflexion.

La fonction \(\log_a x\) étant strictement décroissante et convexe sur tout son domaine pour \(0<a<1 \), elle n'a ni extremum, ni point d'inflexion.

Résumons ce que nous savons de ces fonctions dans un tableau :

  • \(a>1\)

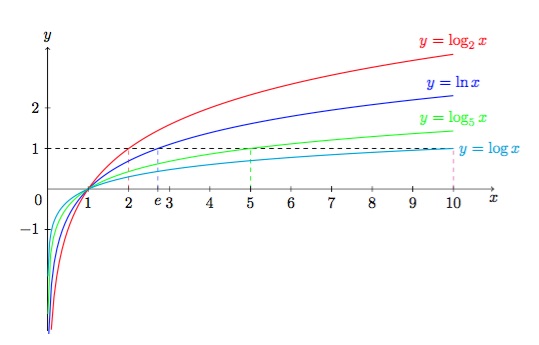
Figure 4 : Graphique de \(\log_2 x \), de \(\ln x \), de \(\log_5 x\) et de \(\log x=\log_{10} x \).

 

  • \(0<a<1\)

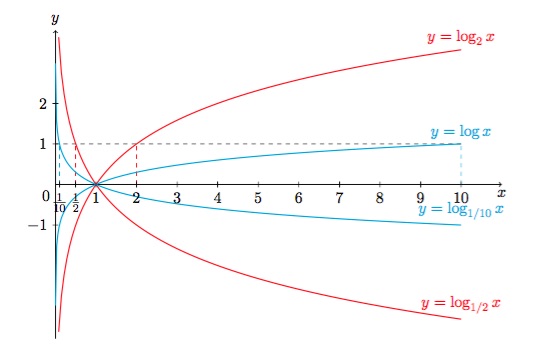
Figure 5 : Graphique de \(\log_{1/10} x \), de \(\log_{1/2} x \), de \(\log_2 x \) et de \(\log x \).

Théorie

Retour au module