Théorie du module : Fonctions

Représentation graphique

En général, les représentations graphiques de fonctions sont réalisées dans un repère cartésien orthonormé. On représente la variable indépendante sur l'axe horizontal (appelé axe \(OX\)) et la variable dépendante sur l'axe vertical (appelé axe \(OY\)).

Autrement dit, le graphique de \(f\) est constitué de l'ensemble des points \((x,y)\) du plan de coordonnées tels que \(y=f(x)\) et \(x\) appartient au domaine de définition de \(f\). La représentation graphique d'une fonction \(f\) nous donne une image intéres\-sante du comportement d'une fonction. Comme, en chaque point \((x,y)\) de la courbe, l'ordonnée \(y\) est égale à la valeur de \(f(x)\), elle peut être lue comme la hauteur de la courbe au point \(x\). Pour trouver les points d'ordonnée \(c\), il suffit donc de tracer la droite \(y=c\) et de regarder ses intersections avec le graphe de la fonction.

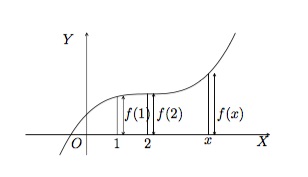
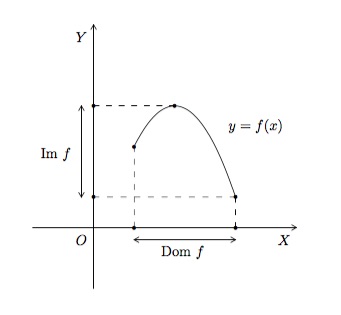
La représentation graphique de \(f\) nous permet aussi de visualiser le domaine de définition et l'ensemble image de f sur les axes \(OX\) et \(OY\) respectivement.

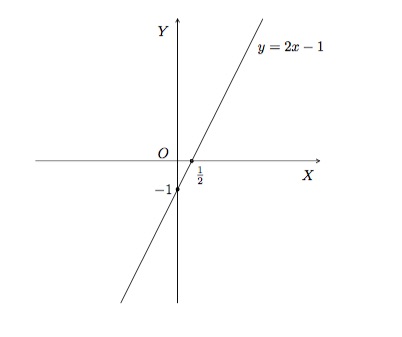
Dessinons la courbe représentative de la fonction \(f(x)=2x-1\). L'équation de la courbe est \(y=2x-1\) et nous y reconnaissons celle d'une droite de pente 2 et d'ordonnée à l'origine \(-1\). Comme l'expression \(2x-1\) est définie pour toutes les valeurs réelles de \(x\), le domaine de définition de \(f\) est tout l'ensemble des nombres réels, noté \(\mathbb{R}\). Le graphique montre que l'ensemble image est aussi \(\mathbb{R}\).

Cherchons le domaine de définition de la fonction \(f(x)=\sqrt{x+2}\). Comme la racine carrée d'un nombre négatif n'est pas définie (en tant que nombre réel), le domaine de définition de \(f\) ne comprend que les valeurs de \(x\) pour lesquelles \(x+2\ge0\). Ce qui est équivalent à \(x\ge -2\). Le domaine de définition est donc l'intervalle \([-2;+\infty[\).

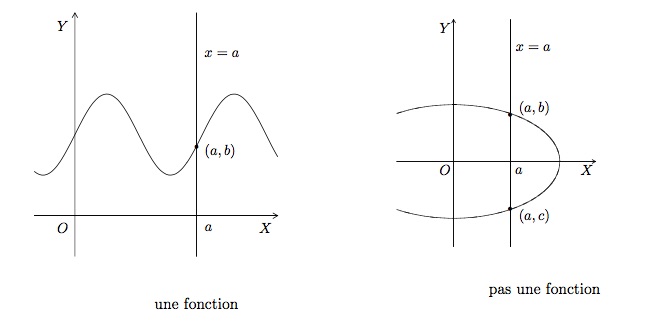
La représentation graphique d'une fonction est une courbe du plan \(OXY\). Pour déterminer les courbes du plan qui sont le graphe d'une fonction, nous pouvons utiliser le test suivant.

En effet, si une droite verticale quelconque \(x=a\) ne coupe une courbe qu'une fois, en \((a,b)\), alors une seule image \(b\) est associée à \(a\) par \(f\). Si au contraire, une droite \(x=a\) coupe une courbe deux fois, en \((a,b)\) et en \((a,c)\), alors cette courbe ne peut être la représentation d'une fonction car une fonction ne peut attribuer deux valeurs différentes à \(a\).

Dans un graphique, on remarque quelques points particuliers.

Une racine est l'abscisse du point d'intersection du graphe avec l'axe \(OX\). Pour trouver les racines, il faut donc résoudre l'équation \(f(x)=0\). 

L'ordonnée à l'origine est l'ordonnée du point d'intersection du graphe avec l'axe \(OY\). Pour la trouver, on remplace \(x\) par \(0\) dans la formule de \(f\), c'est-à-dire on calcule \(f(0)\). 

Pour déterminer le signe d'une fonction, il faut résoudre les inéquations \(f(x)<0\) et \(f(x)>0\).

Pour un rappel concernant les tableaux de signes, cliquez ici.

 Regardons la fonction \(f(x)=\sin{x}\) sur l'intervalle \([-2\pi,2\pi]\).

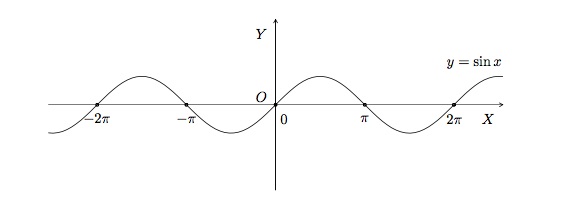
Cette fonction possède 5 racines : \(x=-2\pi\), \(x=-\pi\), \(x=0\), \(x=\pi\) et \(x=2\pi\). Son ordonnée à l'origine est \(y=0\). Elle est positive pour \(x\in\, ]-2\pi,2\pi[\, \) et \(x\in\, ]0,\pi[\, \) et elle est négative pour \(x\in\, ]-\pi,0[\, \) et \(x\in\, ]\pi,2\pi[\, \).

Graphiquement, le maximum correspont à la plus grande valeur d'une fonction et le minimum correspond à la plus petite valeur. 

La fonction \(f(x)=\sin{x}\) sur l'intervalle \([-2\pi,2\pi]\), représentée ci-dessus, a un maximum \(y=1\) et un minimum \(y=-1\). Les valeurs maximales sont atteintes pour \(x=-\frac{3\pi}{2}\) et \(x=\frac{\pi}{2}\) et les valeurs minimales sont atteintes pour \(x=-\frac{\pi}{2}\) et \(x=\frac{3\pi}{2}\).