Théorie du module : Logarithmes et exponentielles
Table des matières
Afficher toute la théorie du moduleFonctions exponentielles
(a) Définition
Nous avons vu que la fonction
\(\ln:\mathbb R^+_0\to\mathbb R:x\mapsto\ln x\)
est une bijection. Ceci implique que pour tout \(a>0\) et \(a\neq 1 \), la fonction
\(\log_a:\mathbb R^+_0\to\mathbb R:x\mapsto\log_ax=\dfrac{\ln x}{\ln a}\)
est également une bijection. La fonction \(\log_a\) a donc une fonction réciproque que nous appellerons fonction exponentielle en base a .
Définition - Soit \(a>0\) et \(a\neq 1 \). La fonction exponentielle en base \(a\), notée \(\exp_a \), est la réciproque de \(\log_a\), c'est-à-dire
\(\exp_a:\mathbb R\to\mathbb R^+_0:x\mapsto\exp_a x,\)
où
\(y=\exp_a x\quad\iff\quad x=\log_a y.\)
Nous avons donc
\(\forall y\in\mathbb R^+_0:\,\exp_a(\log_a y)=y\)
et
\(\forall x\in\mathbb R:\,\log_a(\exp_a x)=x.\)
Comme nous avons vu dans la Propriété 5 de la fonction \(\log_a{x}\) que pour tout \(x\in\mathbb Q \),
\(\log_a a^x=x\log_a a=x,\)
on peut en conclure que pour tout \(x\in\mathbb Q \),
\(\exp_a x=a^x.\)
Cela parait naturel de ne pas se restreindre aux nombres rationnels, mais d'étendre à tous les nombres réels. Ceci nous permet de définir des puissances à exposant réel.
Définition - Soit \(a>0\) et \(a\neq 1 \). On définit pour tout \(x\in\mathbb R\)
\(a^x=\exp_a x.\)
(b) Le cas particulier de l'exponentielle en base e
Nous avons vu que \(\ln x=\log_e x \), où \(e\) est un nombre irrationnel et \(e=2.71828\dots \).
La réciproque de \(\ln x\) est donc \(e^x \).
- La fonction \(e^x \) est dérivable pour tout \(x\in\mathbb R\) et sa dérivée est e^x .
- Toutes les primitives de \(e^x \) sont de la forme
\(e^x+C,\)
où \(C\in\mathbb R\) est une constante arbitraire.
Puisque la fonction \(e^x \) est la réciproque de \(\ln x\) nous savons que
\(f(x)=e^x\iff x=\ln{(f(x))}.\)
-
Dérivons le membre de gauche et de droite de \(x=\ln{(f(x))}\) : la dérivée du membre de gauche est \((x)'=1 \)et la dérivée du membre de droite est \(\left(\ln{(f(x))}\right)'=f'(x)\ln'{(f(x))}=\dfrac{f'(x)}{f(x)} \).
En rassemblant les deux, on peut conclure que \(1=\dfrac{f'(x)}{f(x)}\).
On peut réécrire cette égalité comme
\(f(x)=f'(x),\)et donc
\((e^x)'=f'(x)=f(x)=e^x.\)
-
Le calcul la dérivée de \(e^x+C\) nous donne
\(\left(e^x+C\right)'=e^x+0=e^x.\)Les fonctions de la forme \(e^x+C\) sont donc bien des primitives de \(e^x \). Il n'y en a pas d'autres, car les primitives ne diffèrent que d'une constante.
(c) Propriétés de la fonction exponentielle en base a
Voici des propriétés importantes des fonctions exponentielles en base \(a \).
Propriétés : Soit \(a>0\) et \(a\neq 1 \). Pour tout \(x , y\in\mathbb{R} \), on a
- \(a^x=e^{x\ln a}.\)
-
la fonction \(a^x\) est dérivable et \((a^x)'=a^x\ln a \).
-
\( \displaystyle\left(\dfrac{1}{a}\right)^x=a^{-x}\)
-
\(\displaystyle a^{x+y}=a^x\cdot a^y\)
-
\(\displaystyle\left(a^x\right)^y=a^{xy} \)
En effet,
- on a \(\log_a e^{x\ln a}=\dfrac{\ln e^{x\ln a}}{\ln a}=\dfrac{x\ln a}{\ln a}=x.\) Sachant que \(x=\log_a y\) si et seulement si \(y=a^x \), on en déduit \(e^{x\ln a}=a^x \).
-
nous savons que \(a^x=e^{x\ln a} \) et \(\left(e^x\right)'=e^x \). En utilisant la formule de dérivation des fonctions composées, on obtient
\(\left(a^x\right)'=\left(e^{x\ln a}\right)'=(x\ln a)'e^{x\ln a}=\ln a\cdot e^{x\ln a}=\ln a\cdot a^x=a^x\ln a.\)
-
on a \(x=\log_a a^x \). Sachant que \(\log_a\dfrac{1}{a}=-1 \), on obtient
\(\log_a\left(\dfrac{1}{a}\right)^x=x\log_a\dfrac{1}{a}=x\cdot (-1)=-x=\log_aa^{-x}.\)
Ceci permet de conclure que
\(\left(\dfrac{1}{a}\right)^x=a^{-x}.\)
-
nous savons aussi que \(x+y=\log_a a^{x+y} \) et donc
\(\log_a a^{x+y}=x+y=\log_a a^x+\log_a a^y=\log_a\left(a^x\cdot a^y)\right.\)On peut donc conclure que
\(a^{x+y}=a^x\cdot a^y.\)
-
Finalement l'utilisation de \(\log_ax^p=p\log_ax\) nous permet d'obtenir
\(\log_a\left(a^x\right)^y=y\log_a a^x=yx=xy=\log_a a^{xy}.\)On en conclut que
\(\left(a^x\right)^y=a^{xy}.\)
(d) Représentation graphique de la fonction exponentielle en base a
Nous allons maintenant analyser le comportement de la fonction \(a^x \), où \(a>0\) et \(a\neq 1 \). Nous savons déjà plusieurs choses utiles pour cette analyse :
-
le domaine de la fonction \(a^x \) est \(\mathbb R \),
-
la dérivée : \(\left(a^x\right)'=a^x\ln a \),
-
des valeurs particulières : \(a^0=1\) et \(a^1=a \).
Comme pour la fonction \(\log_a \), nous allons traiter séparément les cas \(a>1\) et \(0<a<1 \).
Propriétés :
- Si \(a>1\), la fonction \(a^x\) est strictement croissante sur tout son domaine.
- Si \(a>1\), la fonction \(a^x\) est convexe sur tout son domaine.
- Si \(a>1\), le graphique de \(a^x\) n'a pas d'asymptote verticale.
- Si \(a>1\), le graphique de \(a^x\) a une asymptote horizontale \(y=0\) en \(-\infty\) et n'a pas d'asymptote horizontale en \(+\infty \).
- Si \(a>1\), le graphique de \(a^x\) n'a pas d'asymptote oblique.
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
Résumons ce que nous savons de ces fonctions dans un tableau :
- \(a>1\)

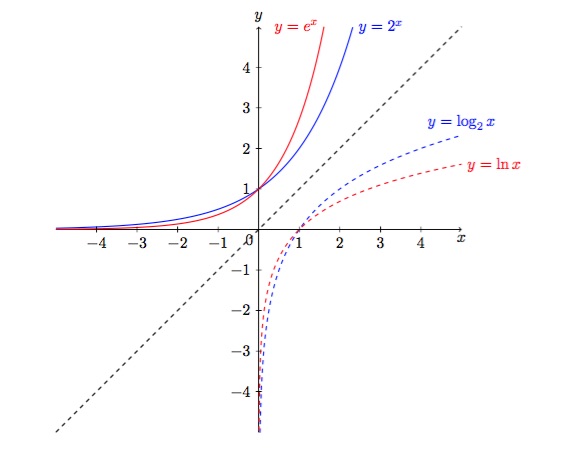
Figure 6 : Graphique de \(2^x \), \(e^x \), \( \log_2 x\) et de \(\ln x \).
Propriétés :
-
Si \(0<a<1 \), la fonction \(a^x\) est strictement décroissante sur tout son domaine.
-
Si \(0<a<1 \), la fonction \(a^x\) est convexe sur tout son domaine.
-
Si \(0<a<1 \), le graphique de \(a^x\) n'a pas d'asymptote verticale.
-
Si \(0<a<1 \), le graphique de \(a^x\) n'a pas d'asymptote horizontale en \(-\infty\) et a une asymptote horizontale \(y=0\) en \(+\infty \).
-
Si \(0<a<1 \), le graphique de \(a^x\) n'a pas d'asymptote oblique.
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
Résumons ce que nous savons de ces fonctions dans un tableau :
- \(0<a<1\)

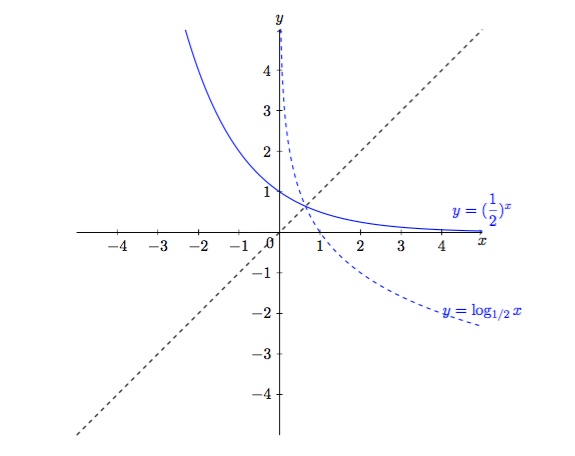
Figure 7 : Graphique de \(\displaystyle \left(\dfrac{1}{2}\right)^x\) et de \(\log_{1/2} x \).
Le graphique de \(a^x\) est l'image de celui de \(\log_ax\) par la symétrie orthogonale par rapport à la droite \(y=x\) (la première bissectrice).
