Théorie du module : Repères et vecteurs
Table des matières
- Le plan \(\mathbb{R}^2\)
- L'espace \(\mathbb{R}^3\)
- La notion de vecteur
- Opérations sur les vecteurs
- Vecteurs et points particuliers
- Exemples détaillés
Opérations sur les vecteurs
Dans les applications, on distingue les grandeurs scalaires par opposition aux grandeurs vectorielles, c'est-à-dire aux vecteurs. Une grandeur scalaire est caractérisée par un seul nombre réel, alors qu'une grandeur vectorielle est caractérisée par deux ou trois nombres réels suivant que l'on se trouve dans le plan ou l'espace. Les opérations que l'on peut effectuer sur des grandeurs scalaires ne sont rien d'autre que celles que l'on peut effectuer sur les nombres réels. Par contre, on définit des opérations spécifiques aux vecteurs.
(a) L'addition vectorielle
On définit l'addition ou somme de deux vecteurs \(\vec{u}\) et \(\vec{v}\), comme le vecteur dont les composantes sont obtenues par addition des composantes correspondantes des deux vecteurs \(\vec{u}\) et \(\vec{v}\). On note \(\overrightarrow{u+v}\) le vecteur somme.
\(\vec{u}+\vec{v}=(u_x+v_x,u_y+v_y).\)
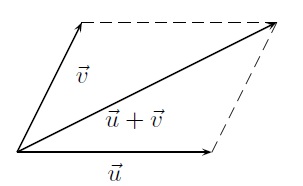
On peut donner une interprétation géométrique de cette opération. On considère le vecteur \(\vec{u}\) placé en n'importe quel point du plan. On place le vecteur \(\vec{v}\) à l'extrémité du vecteur \(\vec{u}\). Les deux vecteurs forment alors les côtés d'un parallélogramme dont la diagonale partant de l'origine de \(\vec{u}\) et arrivant à l'extrémité de \(\vec{v}\) est le vecteur somme \(\vec{u}+\vec{v}\).
\(\vec{u}+\vec{v}=(u_x+v_x,u_y+v_y,u_z+v_z).\)
Par exemple, la somme des deux vecteurs \(\vec{a}=(3,1,4)\) et \(\vec{b}=(1,-2,3)\) est le vecteur \(\vec{a}+\vec{b}=(3+1,1+(-2),4+3)=(4,-1,7)\).
Propriétés de l'addition vectorielle
- L'addition vectorielle est commutative : \(\vec{u} + \vec{v} = \vec{v} + \vec{u}\).
On constate que le vecteur \(\vec{v}+\vec{u}\) que l'on forme en additionnant \(\vec{v}\) et \(\vec{u}\) coïncide avec le vecteur \(\vec{u}+\vec{v}\).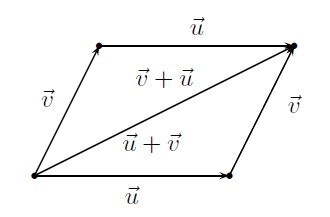
- L'addition vectorielle est associative : \(\vec{u}+(\vec{v}+\vec{w})=(\vec{u} + \vec{v}) + \vec{w}\). On constate que si l'on additionne \(\overrightarrow{OB}=\vec{u}+\vec{v}\) à \(\vec{w}\) on obtient le vecteur \(\overrightarrow{OC}=(\vec{u}+\vec{v})+\vec{w}\). On obtient ce même vecteur en additionnant au vecteur \(\vec{u}\), le vecteur \(\overrightarrow{AC}=\vec{v}+\vec{w}\). D'où \(\vec{u}+(\vec{v} + \vec{w})=(\vec{u} + \vec{v}) + \vec{w}\).
On remarquera que pour additionner \(n\) vecteurs, il suffit en partant d'une position arbitraire du premier vecteur, de placer successivement l'origine de chaque vecteur à l'extrémité du précédent.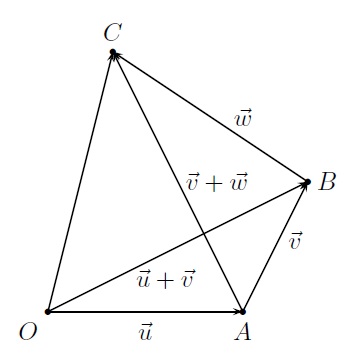
Le vecteur somme des \(n\)vecteurs est alors le vecteur dont l'origine est celle du premier et l'extrémité, celle du dernier. Dans cette opération, l'ordre des vecteurs dans la somme n'a pas d'importance. Cette opération peut se faire aussi bien dans l'espace que dans le plan.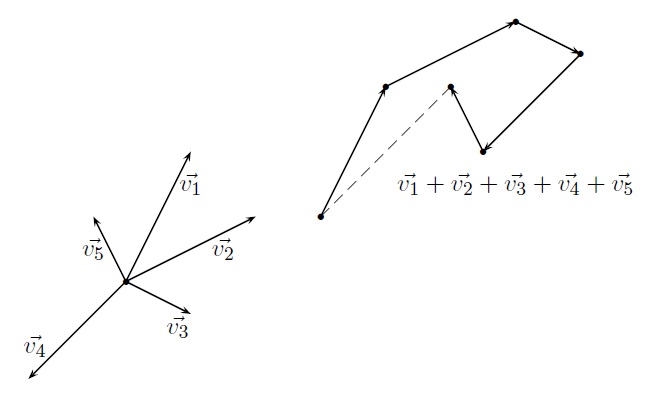
- L'addition vectorielle admet un élément neutre : \(\vec{v} + \vec{o} = \vec{v}\).
L'élément neutre est le vecteur nul ou zéro, noté \(\vec{o}\) et défini comme le vecteur dont toutes les composantes sont égales à zéro. Dans le plan, on a \(\vec{o}=(0,0)\) et dans l'espace \(\vec{o}=(0,0,0)\). Ces vecteurs ont une longueur nulle et par convention leur direction n'est pas définie. - L'addition vectorielle admet un opposé : \(\vec{v} + (-\vec{v})=\vec{o}\).
Le vecteur noté \(-\vec{v}\) et appelé vecteur opposé de \(\vec{v}\), dont les composantes sont les composantes du vecteur \(\vec{v}\), changées de signe. Dans le plan, si \(\vec{v}=(v_x,v_y)\) alors \(-\vec{v}=(-v_x,-v_y)\) et dans l'espace, si \(\vec{v}=(v_x,v_y,v_z)\) alors \(-\vec{v}=(-v_x,-v_y,-v_z)\). Le vecteur \(-\vec{v}\) a la même longueur que \(\vec{v}\), la même direction, mais est de sens opposé.
(b) La soustraction vectorielle
La soustraction vectorielle revient à une addition vectorielle : lorsqu'on veut soustraire le vecteur \(\vec{v}\) du vecteur \(\vec{u}\), on ajoute à \(\vec{u}\) l'opposé de \(\vec{v}\), c'est-à-dire
\(\vec{u}-\vec{v} = \vec{u} + (-\vec{v}).\)
\(\vec{u}-\vec{v}=(u_x-v_x,u_y-v_y).\)
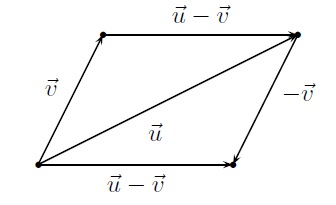
On constate que pour soustraire \(\vec{v}\) de \(\vec{u}\), il suffit de placer sur le même point les origines des deux vecteurs et de prendre comme origine et extrémité du vecteur \(\vec{u}-\vec{v}\) respectivement l'extrémité de \(\vec{v}\) et l'extrémité de \(\vec{u}\).
\(\vec{u}-\vec{v}=(u_x-v_x,u_y-v_y,u_z-v_z).\)
Par exemple, la différence des deux vecteurs \(\vec{a}=(3,1,4)\) et \(\vec{b}=(1,-2,3)\) est le vecteur \(\vec{a}-\vec{b}=(3-1,1-(-2),4-3)=(2,3,1)\).
(c) Multiplication d'un vecteur par un scalaire
La multiplication d'un vecteur \(\vec{v}\) par un scalaire \(\alpha\), notée \(\alpha\vec{v}\), est le vecteur dont les composantes sont celles de \(\vec{v}\) multipliées par \(\alpha\).
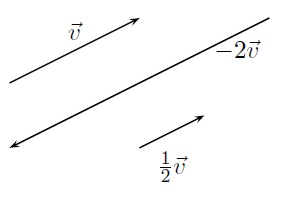
Géométriquement, cette opération revient à effectuer une contraction ou une dilatation du vecteur \(\vec{v}\), avec éventuellement un renversement de sens si le scalaire \(\alpha\) est négatif.
Par exemple, si \(\vec{v}=(1,2,3)\) et \(\alpha =4\) alors \(\alpha\vec{v}=(4,8,12)\).
Propriétés de la multiplication d'un vecteur par un scalaire
- Distributivité par rapport à l'addition dans \(\mathbb{R}\) : \((\alpha + \beta) \vec{v} = \alpha \vec{v} + \beta \vec{v}\).
- Distributivité par rapport à l'addition vectorielle : \(\alpha (\vec{u}+\vec{v}) = \alpha \vec{u} + \alpha \vec{v}\).
- Associativité mixte : \(\alpha (\beta \vec{v}) = (\alpha \beta) \vec{v}\).
- Elément neutre : \(1\cdot \vec{v} = \vec{v}$\).
On dira que deux vecteurs \(\vec{u}\) et \(\vec{v}\) du plan ou de l'espace :
- ont la même direction et sont de même sens si \(vec{u}=\alpha\vec{v}\), pour un certain \(\alpha>0\),
- ont la même direction et sont de sens contraire si \(\vec{u}=\alpha\vec{v}\), pour un certain \(\alpha<0\).
Par exemple, les vecteurs \(\vec{u}=(4,8,12)\) et \(\vec{v}=(1,2,3)\) sont parallèles car \(\vec{u}=4\, \vec{v}\).
(d) Le produit scalaire de deux vecteurs
Il s'agit d'une opération de multiplication entre deux vecteurs donnant comme résultat un scalaire, c'est-à-dire un nombre. Il est noté en général avec un point \(\vec{u}\cdot\vec{v}\). Pour le distinguer de la multiplication usuelle, nous le noterons \(\vec{u}\odot\vec{v}\). Dans un repère orthonormé, le produit scalaire de deux vecteurs est égal à la somme des produits de leurs composantes correspondantes.
\(\vec{u}\odot\vec{v}=u_x v_x + u_y v_y.\)
Dans l'espace, si \(\vec{u}=(u_x,u_y,u_z)\) et \(\vec{v}=(v_x,v_y,v_z)\) alors\(\vec{u}\odot\vec{v}=u_x v_x + u_y v_y + u_z v_z.\)
On appelle ce produit "scalaire" parce que son résultat est un nombre.
Par exemple, le produit scalaire des vecteurs \(\vec{u}=(2,3,4)\) et \(\vec{v}=(1,-2,2)\) est le nombre réel
\(\vec{u}\odot\vec{v}=2\cdot1 +3\cdot(-2)+4\cdot2=4.\)
Propriétés du produit scalaire
- Le produit scalaire d'un vecteur avec lui-même est égal au carré de sa longueur ou norme : \(\vec{v}\odot\vec{v}=\|\vec{v}\|^2.\)
- Le produit scalaire de deux vecteurs est commutatif : \(\vec{u}\odot\vec{v}=\vec{v}\odot\vec{u}.\)
- Il y a distributivité du produit scalaire par rapport à l'addition des vecteurs :
\(\vec{u}\odot(\vec{v}+\vec{w})=\vec{u}\odot\vec{v}+\vec{u}\odot\vec{w}.\) - Il y a associativité mixte : \((\alpha\vec{u})\odot\vec{v}=\alpha(\vec{u}\odot\vec{v})=\vec{u}\odot(\alpha\vec{v}).\)
- Le vecteur nul est absorbant pour le produit scalaire : \(\vec{o}\odot\vec{u}=0.\)
On peut définir le produit scalaire d'un point de vue géométrique.
\(\vec{u}\odot\vec{v}=\|\vec{u}\|\|\vec{v}\|\cos\theta.\)
En d'autres termes, le produit scalaire de deux vecteurs est égal au produit des normes des vecteurs par le cosinus de l'angle entre ceux-ci.
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
De la proposition, on peut déduire la formule suivante pour le cosinus de l'angle \(\theta\) que forment deux vecteurs \(\vec{u}\) et \(\vec{v}\).
Par exemple, l'angle entre les vecteurs \(\vec{a}=(4,-3)\) et \(\vec{b}=(1,2)\) est donné par
\(\cos\theta = \dfrac{\vec{a}\odot\vec{b}}{\|\vec{a}\|\|\vec{b}\|}= \dfrac{-2}{5\sqrt{5}},\)
et donc
\(\theta=\arccos\frac{-2}{5\sqrt{5}}\approx 100,3^\circ.\)
Dans ce cas, le cosinus de l'angle vaut \(0\) et on déduit de la proposition que le produit scalaire est nul.
Par exemple, les vecteurs \(\vec{a}=(\frac{1}{2},-3)\) et \(\vec{b}=(-2,12)\) sont parallèles. En effet, on a
\(\cos\theta = \dfrac{\vec{a}\odot\vec{b}}{\|\vec{a}\|\|\vec{b}\|}= \dfrac{-37}{37}=-1,\)
et donc
\(\theta=\arccos (-1)= \pi.\)
L'angle entre les deux vecteurs étant \(\pi\), ces deux vecteurs sont parallèles. De plus, on remarque que \(\vec{b}= -4 \vec{a}\).
Par contre, les vecteurs \(\vec{a}=(2,3)\) et \(\vec{b}=(6,-4)\) sont orthogonaux car \(\vec{a}\odot\vec{b}=2.6+ 3.(-4)=0\).
On peut démontrer les deux résultats suivants, relatifs à la longueur des vecteurs :
\((1)\) Inégalité de Cauchy-Schwartz : \(|\vec{u}\odot\vec{v}|\le \|\vec{u}\|\|\vec{v}\|\).
\((2)\) Inégalité triangulaire : \(\|\vec{u}+\vec{v}\|\le\|\vec{u}\|+\|\vec{v}\|\).
Cette inégalité spécifie que dans un triangle, la longueur d'un côté ne peut dépasser la somme des longueurs des deux autres côtés.
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
(e) Le produit vectoriel de deux vecteurs
A la différence du produit scalaire, qui est un nombre réel, le produit vectoriel de deux vecteurs est un vecteur, noté \(\vec{u}\times\vec{v}\) (ou encore \(\vec{u}\wedge\vec{v}\)). Pour le définir, on a besoin de la notion d'orientation d'un repère.
- \(\vec{u}\times\vec{v}\) est perpendiculaire à \(\vec{u}\) et à \(\vec{v}\);
- \(\|\vec{u}\times\vec{v}\|=\|\vec{u}\|\|\vec{v}\|\, |\sin{\theta}| \)
- les vecteurs \(\vec{u}\), \(\vec{v}\) et \(\vec{u}\times\vec{v}\)pris dans cet ordre forment un repère d'orientation directe.
Remarque : La longueur \(\|\vec{u}\times\vec{v}\|\) est l'aire du parallélogramme construit sur les vecteurs \(\vec{u}\) et \(\vec{v}\).
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
Propriétés du produit vectoriel
- Le produit vectoriel de deux vecteurs est anti-commutatif : \(\vec{u}\times\vec{v}=-(\vec{v}\times\vec{u}).\)
- Le produit vectoriel est linéaire à gauche : \(\vec{u}\times(\alpha\vec{v}+\beta\vec{w})=\alpha(\vec{u}\times\vec{v})+\beta(\vec{u}\times\vec{w}).\)
- Le produit vectoriel est linéaire à droite : \((\alpha\vec{u}+\beta\vec{v})\times\vec{w}=\alpha(\vec{u}\times\vec{w})+\beta(\vec{v}\times\vec{w}).\)
\(\vec{u}\times\vec{v}=(u_yv_z-u_zv_y,u_zv_x-u_xv_z, u_xv_y-u_yv_x).\)
Par exemple, si \(\vec{a}=(1,2,3)\) et \(\vec{b}=(6,5,4)\) alors le vecteur \(\vec{v}=\vec{a}\times \vec{b}=(2\cdot 4-3\cdot 5,3\cdot 6-1\cdot 4, 1\cdot 5-2\cdot 6)=(-7,14,-7)\) est perpendiculaire aux vecteurs \(\vec{a}\) et \(\vec{b}\). L'aire du parallélogramme construit sur \(\vec{a}\) et \(\vec{b}\). est
\(\|\vec{a}\times \vec{b}\|=\|\vec{v}\|=\sqrt{49+196+49}=\sqrt{294}=7\sqrt{6}.\)
Dans le cas où les deux vecteurs sont parallèles, le sinus de l'angle vaut \(0\) et on en déduit que le produit vectoriel est nul.
Par exemple, les vecteurs \(\vec{u}=(1,-2,3)\) et \(\vec{v}=(-2,4,-6)\)sont parallèles car
\(\vec{u}\times\vec{v}=(-2\cdot (-6)-3\cdot 4,3\cdot (-2)-(-6)\cdot 1, 1\cdot 4-(-2)\cdot (-2))=(0,0,0)=\vec{o}.\)
On a \(\vec{v}=-2\vec{u}\).
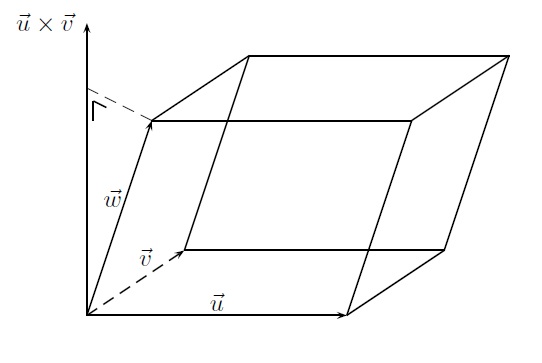
(f) Produit mixte
Si on dispose de 3 vecteurs donnés \(\vec u, \vec v \) et \(\vec w \), on peut considérer l'expression
\((\vec u \times \vec v) \odot \vec w \)
qui désigne un nombre réel, appelé produit mixte des 3 vecteurs .
Dans un repère cartésien orthonormé, on peut donner une signification géométrique intéressante à \(| (\vec u \times \vec v) \odot \vec w |\). En effet, ce nombre revient à \(\| \vec u \times \vec v \| \| \vec w \| | \cos (\vec u \times \vec v, \vec w ) | \). Si nous regardons le parallélipipède construit sur les 3 vecteurs, nous observons que \(\| \vec u \times \vec v \|\) donne l'aire de la base (construite sur \(\vec u\) et \(\vec v\)) et que \(\| \vec w \| |\cos (\vec u \times \vec v, \vec w)|\) donne la longueur de la projection orthogonale de \(\vec w \) sur la droite qui porte \(\vec u \times \vec v\), c'est-à-dire la hauteur du parallélipipède. Donc \(|(\vec u \times \vec v) \odot \vec w|\) donne le volume du parallélipipède.