Théorie du module : Repères et vecteurs
Table des matières
- Le plan \(\mathbb{R}^2\)
- L'espace \(\mathbb{R}^3\)
- La notion de vecteur
- Opérations sur les vecteurs
- Vecteurs et points particuliers
- Exemples détaillés
L'espace \(\mathbb{R}^3\)
(a) Repère
Dans les sections précédentes, nous avons travaillé dans le plan. Si l'on veut travailler dans l'espace à trois dimensions, il faut considérer 3 axes. Un repère dans l'espace est constitué de trois droites sécantes, chacune munie d'une unité de longueur, et qui se coupent en leur point origine. Ces trois doites sont l'axe des \(x\), l'axe des \(y\) et l'axe des \(z\). Lorsque les trois droites dont perpendiculaires deux à deux et munies de la même unité de longueur, on parle de repère cartésien orthonormé. En général, les axes des \(y\) et des \(z\) se trouvent dans le plan de la feuille et celui des \(x\) se projette vers l'avant.
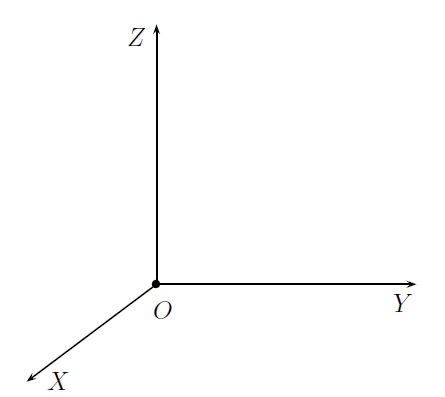
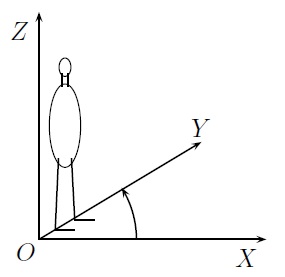
Ainsi placés, ces 3 axes déterminent un système de coordonnées droit ou d'orientation directe. On dit que le repère formé par les axes \(OX\), \(OY\) et \(OZ\) est d'orientation directe si un spectateur "debout" sur le plan \(OXY\), les pieds en \(O\) et la tête en \(Z\), observe que pour amener la droite \(OX\) sur la droite \(OY\), il doit faire une rotation dans le sens antihorlogique (on regarde le plus petit angle possible). Dans le cas contraire, le repère est dit d'orientation rétrograde.
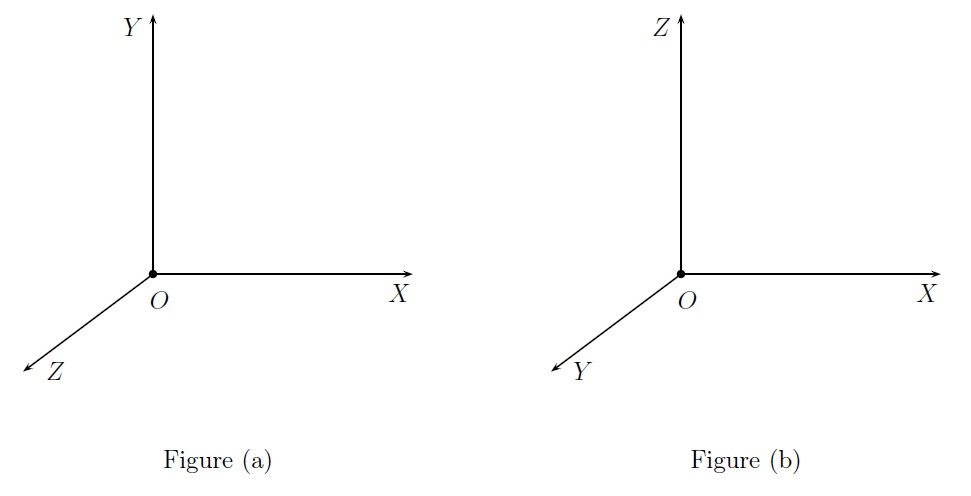
Remarque : Notons que pour savoir si un repère est direct ou rétrograde, l'ordre dans lequel on place les axes est important. Si on permute 2 axes, on change l'orientation du repère. On la change aussi quand on change la direction des axes. Par exemple le repère de la Figure (a) est d'orientation directe tandis que le repère de la Figure (b) est d'orientation rétrograde.
(b) Coordonnées cartésiennes
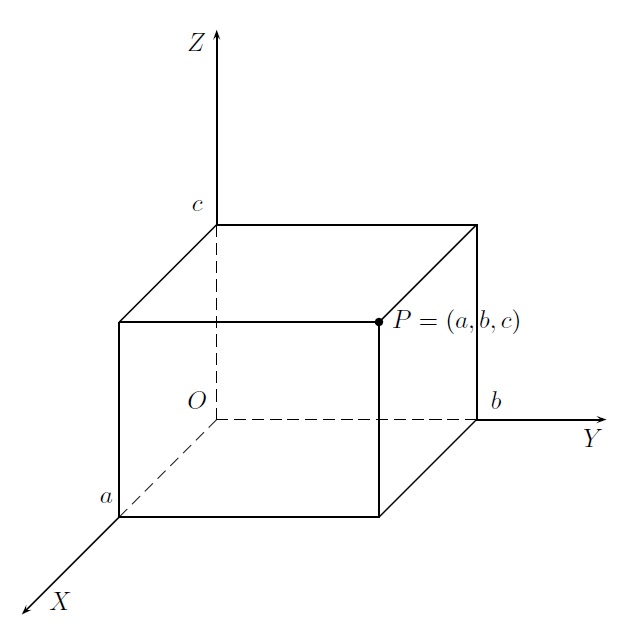
D'un point \(P\) quelconque de l'espace, on mène des parallèles aux axes qui coupent ceux-ci en \(a\) pour l'axe des \(x\), en \(b\) pour l'axe des \(y\) et en \(c\) pour l'axe des \(z\). Le point \(P\) est ainsi associé au triple de nombres réels \((a,b,c)\) qui sont les coordonnées cartésiennes du point \(P\).
(c) Notion de distance
\(d(P,Q)= \sqrt{(x_q -x_p)^2 + (y_q-y_p)^2+(z_q-z_p)^2}.\)
Cette formule provient d'une double application du Théorème de Pythagore. Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
En particulier, la distance d'un point \(P=(x_p,y_p,z_p)\) à l'origine est donnée par \(\sqrt {x_p^2 +y_p^2+z_p^2}\).
Application : Equation de la sphère
Dans l'espace, on se donne un point \(C\) et un nombre \(r>0\).
\(d(P,C)=r.\)
Pour établir l'équation cartésienne de la sphère, on se place dans un repère. Les coordonnées du point \(C\) dans ce repère sont \((x_c,y_c,z_c)\). Soit \(P=(x,y,z)\), un point de la sphère. Puisque \(d(P,C)=r\), on a
\(\sqrt{(x-x_c)^2+(y-y_c)^2+(z-z_c)^2}=r.\)
\((x-x_c)^2+(y-y_c)^2+(z-z_c)^2=r^2.\)
En particulier, l'équation de la sphère centré en \((0,0,0)\) et de rayon \(r\) est\(x^2+y^2+z^2=r^2.\)
(d) Coordonnées cylindriques
Pour obtenir les coordonnées cylindriques, on garde une des coordonnées cartésiennes, par exemple \(z\), et, dans le plan de coordonnées correspondant aux 2 autres on passe aux coordonnées polaires. Un point \(P\) se trouvera ainsi repéré par
- la cote \(z\),
- les coordonnées polaires \(r\) et \(\theta\) de sa projection orthogonale dans le plan \(OXY\).
Ce type de coordonnées est indiqué pour une surface dont les coupes horizontales sont des cercles centrés sur l'axe \(OZ\). Voici quelques exemples :
Un cylindre circulaire droit d'axe \(OZ\) et de rayon \(R\) sera décrit par l'équation \(r = R\).
Une surface de révolution engendrée par la rotation autour de \(OZ\) du graphe d'une fonction \(f : I \rightarrow \mathbb{R}^+ \); \(z \rightarrow f(z)\) sera décrite par \(r = f(z)\) simplement. Par exemple, le paraboloïde \(z = \frac{x^2 }{a^2 } + \frac{y^2}{a^2}\) sera décrit par \(r = a \sqrt{z}\).
Ces coordonnées sont souvent utilisées en physique pour l'étude de mouvements de rotation par exemple.
(e) Coordonnées sphériques
Pour préciser la position d'un point sur la surface terrestre, on donne la longitude et la latitude. Les coordonnées sphériques vont dans ce sens.
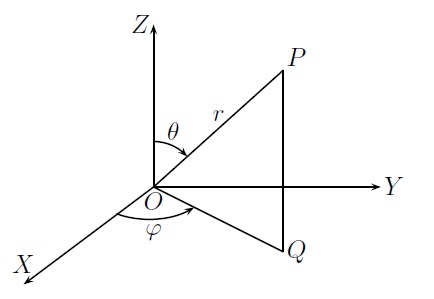
Pour préciser la position d'un point \(P\) dans l'espace, on peut donner les trois quantités suivantes :
- la distance du point \(P\) à l'origine, notée \(r\) (\(r>0\)),
- l'angle que fait le demi-plan comprenant \(OZ\) et \(P\) avec le demi-plan \(OXZ\), appelé longitude et noté \(\varphi\),
- l'angle que fait \(OP\) avec \(OZ\), appelé co-latitude et noté \(\theta\) (la latitude se compte à partir de l'équateur).
Le lien avec les coordonnées cartésiennes est donné par les équations
\(\left\{ \begin{array}{l} x = r \sin \theta \cos \varphi\\ y = r \sin \theta \sin \varphi\\ z = r \cos \theta \end{array} \right.\)
Voici quelques exemples :
La sphère de centre \(O\) et de rayon \(R\) est décrite par l'équation \(r = R\).
Un demi-plan issu de \(OZ\) sera décrit par \(\varphi = \alpha\) (\(\alpha\) donné).
Un cône de révolution d'axe \(OZ\) sera décrit par \(\theta = \alpha\) (\(\alpha\) donné).
