Travaillons dans l'espace. Soit \(\vec{u}=(u_x,u_y,u_z)\) et \(\vec{v}=(v_x,v_y,v_z)\).

Cas 1 : Les vecteurs \(\vec{u}\) et \(\vec{v}\) ne sont pas colinéaires.

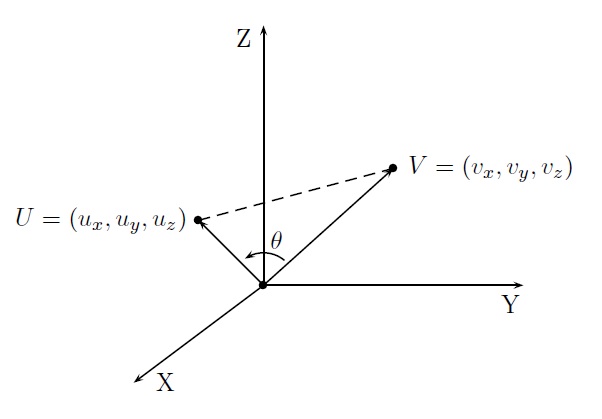
La Règle des cosinus permet d'écrire

\(\|\overrightarrow{UV}\|^2=\|\vec{u}\|^2+\|\vec{v}\|^2-2\|\vec{u}\|\|\vec{v}\|\cos\theta.\)

D'où

\((v_x-u_x)^2 + (v_y-u_y)^2 + (v_z-u_z)^2= (u_x^2+u_y^2+u_z^2)+(v_x^2+v_y^2+v_z^2)-2\|\vec{u}\|\|\vec{v}\|\cos\theta.\)

On peut simplifier cette dernière expression en

\(-2u_xv_x-2u_yv_y-2u_zv_z=-2\|\vec{u}\|\|\vec{v}\|\cos\theta,\)

ce qui par division des deux membres par \(-2\) donne le résultat recherché.

Cas 2 : Les vecteurs \(\vec{u}\) et \(\vec{v}\) sont colinéaires, c'est-à-dire il existe \(\alpha\in \mathbb{R}\) tel que \(\vec{v} = \alpha\vec{u}\). On a en vertu des propriétés du produit scalaire,

\(\vec{u}\odot\vec{v}=\vec{u}\odot(\alpha\vec{u})= \alpha(\vec{u}\odot\vec{u})=\alpha\|\vec{u}\|^2.\)

De même, on a

\(\|\vec{u}\|\|\vec{v}\|\cos\theta=\|\vec{u}\|\|\alpha\vec{u}\|\cos\theta =|\alpha|\|\vec{u}\|^2\cos\theta.\)

Si \(\alpha>0\), alors \(|\alpha|=\alpha\), \(\theta=0\) et \(|\alpha|\|\vec{u}\|^2\cos\theta=\alpha\|\vec{u}\|^2=\vec{u}\odot\vec{v}\).

Si \(\alpha<0\), alors \(|\alpha|=-\alpha\), \(\theta=\pi\) et \(|\alpha|\|\vec{u}\|^2\cos\theta=-\alpha\|\vec{u}\|^2\cdot(-1)=\alpha\|\vec{u}\|^2=\vec{u}\odot\vec{v}\).

\((1)\) En utilisant la Proposition, on obtient

\(\begin{array}{rcl} |\vec{u}\odot \vec{v}|&=&|\, \|\vec{u}\|\|\vec{v}\|\cos{\theta}|\\ &=&\|\vec{u}\|\|\vec{v}\||\cos{\theta}|\\ &\leq&\|\vec{u}\|\|\vec{v}\|. \end{array}\)

\((2)\) En utilisant l'inégalité ci-dessus et les propriétés du produit scalaire, on obtient

\(\begin{array}{rcl} \|\vec{u}+\vec{v}\|^2&=&(\vec{u}+\vec{v})\odot (\vec{u}+\vec{v})\\ &=&\vec{u}\odot \vec{u}+\vec{u}\odot \vec{v}+\vec{v}\odot \vec{u}+\vec{v}\odot \vec{v}\\ &=&\|\vec{u}\|^2+2\, \vec{u}\odot \vec{v}+\|\vec{v}\|^2\\ &\leq&\|\vec{u}\|^2+2\, \|\vec{u}\|\, \|\vec{v}\|+\|\vec{v}\|^2\\ &=&(\|\vec{u}\|+\|\vec{v}\|)^2. \end{array}\)

En prenant la racine carrée des deux membres (qui sont positifs), on trouve

\(\|\vec{u}+\vec{v}\|\le\|\vec{u}\|+\|\vec{v}\|. \)

Construisons la figure suivante :

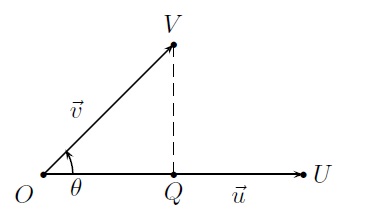
Soit \(Q\) la projection orthogonale de \(V\) sur \(\vec{u}\).
La longueur \(\|\overrightarrow{QV}\|\) représente la hauteur du parallélogramme construit sur \(\vec{u}\) et \(\vec{v}\). L'aire de ce parallélogramme est donc donnée par \(\|\vec{u}\|\cdot\|\overrightarrow{QV}\|\) et comme

\(|\sin{\theta}|=\frac{\|\overrightarrow{QV}\|}{\|\overrightarrow{OV}\|}=\frac{\|\overrightarrow{QV}\|}{\|\vec{v}\|},\)

on obtient

\(\mbox{Aire}=\|\vec{u}\|\, \|\vec{v}\|\, |\sin{\theta}|=\|\vec{u}\times\vec{v}\|.\)

Construisons la figure suivante :

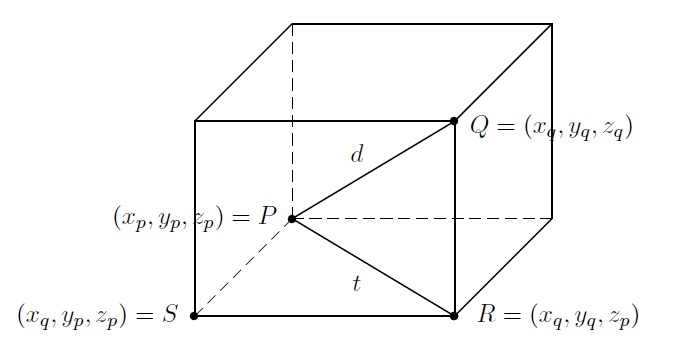
Si \(P=(x_p,y_p,z_p)\) et \(Q=(x_q,y_q,z_q)\) alors on a \(R=(x_q,y_q,z_p)\) et \(S=(x_q,y_p,z_p)\).
Dans le plan \(PSR\), le triangle \(PSR\) est rectangle en \(S\) et par le Théorème de Pythagore, on obtient

\(t^2=(x_q-x_p)^2+(y_q-y_p)^2.\)

Dans le plan \(PQR\), le triangle \(PQR\) est rectangle en \(R\) et par le Théorème de Pythagore, on obtient

\(d^2=t^2+(z_q-z_p)^2.\)

Finalement, on a

\(d^2=(x_q-x_p)^2+(y_q-y_p)^2+(z_q-z_p)^2.\)