Théorie du module : Statistiques descriptives

Définitions et exemples

La statistique est une branche des sciences mathématiques dont l'objet est la collection, l'analyse, l'interprétation et la présentation de données.  Les outils statistiques peuvent s'appliquer dans toutes les disciplines :

1. Les autorités administratives d'une université désirent étudier les taux d'échec (et de succès) des étudiants s'inscrivant en première année de médecine.

2. Un grand recensement est organisé dans la ville d'Ath (Belgique) afin d'étudier la population (âge, sexe, emploi, ...).

3. Le département des resources humaines d'une grande entreprise souhaite évaluer l'opinion générale de ses employés face à un ajustement des horaires de la cafétaria.

4. L'équipe de campagne d'un parti politique cherche à connaître les intentions de vote des habitants de la ville de Comblain pour la prochaine élection communale.

5. Un constructeur automobile souhaite évaluer la distance de freinage sur route sèche de son nouveau modèle de berline 5 places équipée d'un certain type de pneus.

6. La haute autorité de surveillance des jeux de hasard estime que les montants pariés sur la rencontre de football opposant les clubs de Tamines et de Bièvre (clubs de Promotion D) sont anormalement élevés; elle souhaite donc évaluer la probabilité de fraude.

7. Dans un essai clinique, les autorités sanitaires souhaitent déterminer laquelle de deux procédures thérapeutiques est la plus efficace.

De multiples autres exemples sont imaginables.  La statistique descriptive est la branche des statistiques qui regroupe les nombreuses techniques utilisées pour synthétiser, décrire, présenter et interpréter un ensemble conséquent de données.

Au départ de toute étude statistique il y a une étape fondamentale qui concerne la collecte des données. Dans ce chapitre nous supposerons que les données sont toujours disponibles et représentatives du phénomène que nous cherchons à étudier.  Il faut distinguer deux cas : lorsqu'on travaille sur des données qui contiennent toute l'information sur tous les individus de la population concernée par l'étude (comme dans les exemples 1. et 2. ci-dessus), on parlera de statistique déductive. Lorsque les données ne concernent qu'une partie de la population (exemples 3. à 7.) et qu'on souhaite utiliser les statistiques descriptives sur cet échantillon pour déterminer les propriétés du phénomène observé, on parle de statistique inférentielle.  Dans ce chapitre nous n'aborderons que les statistiques déductives.

Le terme de "population", en statistique, désigne bien plus qu'une collection d'êtres humains (ou même d'êtres vivants) : il peut également s'agir d'objets, d'immeubles, d'opinions, de logements, etc.

Par exemple, au 1er septembre 2012 la Belgique comptait 11.116.243 habitants (Source : Statistiques du gouvernement Belge, statbel.fgov.be, 1 septembre 2012). Une étude sur "les Belges" porterait donc sur une population contenant 11.116.243 individus.

 En général la population entière n'est pas disponible. Dans ce cas on étudie plutôt un sous-ensemble de la population, appelé échantillon.

Par exemple, au 1er janvier 2012 la ville d'Arlon comptait 28.289 habitants (Source : http://en.wi\-ki\-pe\-dia.org/wiki/Arlon); ils forment un échantillon de la population belge. De même, les habitants de la rue de Viville forment un échantillon de la population des habitants d'Arlon.

Lorsqu'on étudie une population on s'intéresse à certaines caractéristiques bien précises, appelées variables (ou caractères) statistiques.

Par exemple, le personnel d'une entreprise peut être décrit selon : l' âge, le sexe, la qualification, l'ancienneté dans l'entreprise, la commune de résidence; un lot de pièces mécaniques peut être décrit suivant le poids des pièces, leur diamètre, leur provenance géographique, etc.

Les différentes formes que peut prendre la variable sont appelées ses modalités. Ces modalités doivent être incompatibles (une variable ne peut pas prendre deux modalités en même temps) et exhaustives (toutes les options possibles doivent être disponibles).

Par exemple, les modalités de la variable "âge (en année)" sont \(0, 1, 2, \ldots\). Les modalités de la variable "sexe" sont "M, F". Les modalités de la variable "nombre d'enfants" sont \(0, 1, 2, 3, \ldots\) . Les modalités de la variable "état civil" sont "célibataire, marié, veuf, divorcé, autre".

Au vu de l'exemple précédent il est clair qu'il faut distinguer deux types de variables : les variables qualitatives, c'est-à-dire qui ne sont pas décrites par un nombre mais plutôt par une catégorie (comme le sexe, l'état civil, ...) et les variables quantitatives, c'est-à-dire qui sont décrites par des nombres (comme l' âge, le nombre d'enfants, ...).

Il y a deux types de variables qualitatives : celles dont les modalités peuvent être assignées à un ordre naturel et celles pour lesquelles il n'existe pas d'ordre naturel et qui seront donc classées de façon arbitraire.

Par exemple, le tableau ci-dessous contient les différentes modalités de la variable "Profession" telles que définies par l'INSEE (Institut National de Statistiques et d'Etudes Economiques, France) -- Source Insee, PCS-2003 (E.~Bressoud and J.-C. Kahané. Statistique descriptive (2008)).

 

Code	Catégorie
1.	Agriculteurs exploitants
2.	Artisans, commerçants et chefs d'entreprise
3.	Cadres et professions intellectuelles supérieures
4.	Professions intérimaires
5.	Employés
6.	Ouvriers
7.	Retraités
8.	Autres personnes sans activité professionnelle

 

A chaque catégorie est associé un numéro (entre 1 et 8). Cette association est arbitraire car il n'y pas de notion d'ordre naturel qui s'impose dans ce cas. On parle donc de variable nominale.

Autre exemple, lors d'une prise d'avis pédagogique les choix de réponse sont généralement : "sans objet (SO)", "très défavorable (TD)", "défavorable (D)", "satisfaisant (S)", "favorable (F)", "très favorable (TF)". On attribue généralement à chaque choix de réponse une valeur numérique. On pourrait par exemple décider de les classer de 0 (SO) à 5 (TF). Ce choix est naturel et interprétable (on peut par exemple prendre le score moyen) : la variable "réponse" est donc une variable qualitative ordinale.

Par exemple, les variables suivantes sont quantitatives.

1. Nombre de mariages en Belgique par année.
2. Nombre de faillites en Belgique par semestre.
3. Périmètre crânien d'un nouveau-né.
4. Pluviométrie à un point donné de l'espace.

Si une variable n'est pas qualitative elle est nécessairement quantitative. Il y a deux types de variables quantitatives : celles dont les modalités sont dénombrables (exemples 1. et 2. ci-dessus), et celles dont les modalités sont indénombrables (exemples 3. et 4. ci-dessus).

Considérons une variable continue prenant ses valeurs dans un intervalle \(I \). On appelle discrétisation de la variable le fait de ranger les valeurs en différentes classes

\(C_1, C_2, \ldots, C_M\)

avec les \(C_i \) disjoints (\(C_i \cap C_j = \emptyset\) pour \(i\neq j\) ) et \(C_1 \cup C_2 \cup \ldots \cup C_M = I\)  (de sorte que les différentes classes contiennent toutes les modalités possibles de la variable).

Par exemple, on s'intéresse à la structure par âges de la population féminine en France métropolitaine à une date donnée -- Source INSEE, bilan démographique 2006 (E.~Bressoud and J.-C. Kahané. Statistique descriptive (2008)).

Age	Fréquence
Moins de 15 ans	17,5 %
15 - 24 ans	12,3 %
25 - 34 ans	12,7 %
35 - 44 ans	14,0 %
45 - 54 ans	13,6 %
55 - 64 ans	11,1 %
65 - 74 ans	8,6 %
75 ans ou +	9,1 %

 

Les modalités de la variable âge sont tous les nombres réels plus grand que 0. Ces âges sont rangés (sans grande perte d'information) par classes. Notez que les classes ne sont pas de même amplitude.

Préparation des données -- observations et modalités

La première étape dans l'analyse statistique d'un jeu de données consiste en la transformation du jeu de données brutes en un tableau exploitable du point de vue de l'interprétation statistique. Toute étude statistique démarre avec un jeu de données

\(x_1, x_2, \ldots, x_n,\)

ces données étant mesurées sur la population d'intérêt. Le jeu de données est généralement appelé échantillon ou échantillon observé; ses éléments sont appelés les observations. Le nombre \(n\) d'observations est appelé la taille de l'échantillon.

Par exemple, on s'intéresse au prix (en dollars) de la location d'un studio à Greenwich Village, New York USA. Pour ce faire on note les prix de location de 200 studios, cf Table ci-dessous (Source -- Schaum's Easy Outlines Business Statistics, page 13). On a donc un échantillon de taille 200; les observations sont les différents prix de location.

 

350 370 375 380 390 385 405 400 390 390 400 410 420 435 415 410 410 420 435 415 410 440 450 465 445 435 460 455 440 460 455 435 460 455 470 480 485 475 495 480 490 470 470 470 470 470 470 485 475 495 480 490 470 470 470 485 475 495 480 495 480 490 485 470 470 470 470 500 510 500 515 500 500 505 500 520 500 500 505 520 525 520 500 505 520 525 520 500 500 500 525 500 505 520 525 520 500 500 505 520 525 520 500 505 520 525 520 535 530 540 550 555 545 555 530 535 535 535 535 555 545 555 530 535 535 535 535 535 535 535 535 555 545 555 530 535 535 555 545 555 530 535 560 570 580 585 565 575 565 560 560 560 560 585 560 580 585 565 575 565 560 560 565 575 560 560 580 585 565 575 565 560 595 600 605 610 615 610 595 600 615 605 590 600 590 605 590 615 620 625 635 646 620 640 625 620 645 640 635 630

Table 1 : Liste brute des prix de location de 200 studios à Greenwich village, New York, USA (en dollars).

 

La première étape du tri d'un jeu de données brutes consiste à déterminer les différentes modalités de la variable mesurée; généralement on classe ces modalités par ordre croissant.  On passe donc d'un jeu \(n\) données appelé échantillon ou population à un ensemble de \(M\) modalités

\(y_1, y_2, \ldots, y_M\)

différentes.

Reprenons la Table 1 ci-dessus . La variable prix prend 50 modalités différentes qui sont données dans la Table suivante.

 

350 370 380 390 400 405 410 415 420 435 440 445 450 455 460 470 475 480 485 490 495 500 505 510 520 525 530 535 545 550 555 560 565 570 575 580 585 590 595 600 605 610 615 620 625 630 635 640 645 646

Table 2 : Les 50 modalités différentes de la variable prix de l'échantillon donné dans la Table 1.

 

Dans le cas de variables quantitatives continues ou discrètes avec un nombre élevé de modalités différentes, il est d'abord nécessaire de ranger les modalités par classes.

Par exemple, la Table 2 est peu lisible : il reste trop de modalités différentes. On préférera donc ranger les valeurs par classes, en prenant par exemple

\(\begin{array}{lllll} C_1 = [350,380[, C_2=[380,410[, C_3=[410,440[, C_4=[440,470[, C_5=[470,500[, \\ C_6=[500,530[, C_7=[530,560[, C_8=[560,590[, C_9=[590,620[, C_{10}=[620,650[. \end{array}\)

Le choix du nombre de classes est arbitraire et on pourrait très bien prendre

\(\begin{array}{ll} C_1 = [350, 470[, C_2= [470, 500[, \\ C_3=[500, 530[, C_4=[530, 560[,\\ C_5=[560, 590[, C_6 \mbox{ contenant toutes les valeurs plus grandes que 590}. \end{array}\)

Le choix du nombre de classes est arbitraire. On veille en général à choisir le nombre de classes de façon à ne pas perdre trop d'informations.

Par exemple, considérons à nouveau la Table 1. Si nous ne prenons qu'une seule classe alors nous tentons de résumer le tableau en disant qu'il y a 200 prix entre 350 et 650 dollars; ceci est peu informatif. On préférera donc prendre un nombre de classes plus élevé.

Remarque : Il existe des règles empiriques aidant à choisir le nombre de classes le plus approprié, comme par exemple la règle de Sturges qui suggère de prendre \(M=\log_2n \).

Distribution des données -- fréquences et effectifs

Une fois le jeu de données rangé et les modalités (ou classes de modalités) connues, la première activité de la statistique consiste à recenser le nombre d'individus présentant une modalité déterminée d'une variable.

 

\(\begin{array}{|c|c||c|c|} \hline \textbf{Modalité} & \textbf{Effectif} & \textbf{Modalité} & \textbf{Effectif}\\ \hline 350 & 1 & 370& 2\\ 380& 1 & 390& 4\\ 400& 2 & 405& 1\\ 410& 4 & 415& 2\\ 420& 3 & 435& 3\\ 440& 2 & 445& 1\\ 450& 2 & 455& 2\\ 460& 4 & 470& 14\\ 475& 2 & 480& 6\\ 485& 4 & 490& 3\\ 495& 4 & 500& 14\\ 505& 8 & 510& 2\\ 520& 10 & 525& 6\\ 530& 6 & 535& 17\\ 545& 5 & 550& 1\\ 555& 6 & 560& 9\\ 565& 7 & 570& 2\\ 575& 5 & 580& 2\\ 585& 5 & 590& 2\\ 595& 2 & 600& 5\\ 605& 2 & 610& 2\\ 615& 3 & 620& 3\\ 625& 3 & 630& 1\\ 635& 2 & 640& 2\\ 645& 2 & 646& 1\\ \hline \end{array}\)

Table 3 : Les 50 modalités du prix de location (1ère et 3ème colonne) de 200 studios à Greenwich village (en dollars) de la Table 2 avec leurs effectifs respectifs (2ème et 4ème colonne).

 

Si l'effectif total de la population (de l'échantillon) est \(n\) et si le nombre de modalités (ou le nombre de classes) différentes est \(M\) on a alors nécessairement

\(n =n_1+n_2+ \ldots + n_M=\displaystyle \sum_{i=1}^M n_i.\,\, (1)\)

Remarque : On exprime généralement les fréquences comme des nombres décimaux; en les multipliant par 100 on obtient de manière équivalente leur expression sous forme de pourcentage.

 

Si \(f_i \) désigne la fréquence de la modalité \(x_i\) alors on calcule

\(\displaystyle\sum_{i=1}^Mf_i = \sum_{i=1}^M (n_i/n )= (\sum_{i=1}^M n_i)/n = n / n = 1\)

où nous utilisons l'égalité \((1)\) à l'avant-dernière étape. On déduit

\(\displaystyle\sum_{i=1}^Mf_i = 1\)

ce qui revient à dire que l'hypothèse d'exhaustivité des modalités est respectée. Remarquez qu'on a nécessairement \( 0\le f_i \le 1\) pour tout \(1\le i \le M \).

Des exemples de calcul d'effectifs et de fréquences sont donnés dans les Tables 4, 5, 6 et  7.

 

\(\begin{array}{|c|c| } \hline \textbf{Classe} & \textbf{Effectif} \\ \hline [350,380[ &3 \\ [380,410[ &8 \\ [410,440[ &10\\ [440,470[ &13 \\ [470,500[ &33 \\ [500,530[ &40\\ [530,560[ &35 \\ [560,590[ &30 \\ [590,620[ &16 \\ [620,650[ &12 \\ \hline \textbf{Total} & 200 \\ \hline \end{array}\)

Table 4 : Prix de location (colonne de gauche) de 200 studios à Greenwich village (en dollars) rangés par classes de prix; la colonne de droite contient le nombre de prix de location appartenant à chaque intervalle.

 

\(\begin{array}{|c|ccc| } \hline \textbf{Classe} & \textbf{Amplitude} & \textbf{Centre} & \textbf{Effectif} \\ \hline [350,380[ & 30 & 365 &3 \\ [380,410[ &30 & 395 &8 \\ [410,440[ & 30 & 425 &10\\ [440,470[ & 30 & 455 &13 \\ [470,500[ & 30 & 485 &33 \\ [500,530[ & 30 & 515 &40\\ [530,560[ & 30 & 545 &35 \\ [560,590[ & 30 & 575 &30 \\ [590,620[ & 30 & 605 &16 \\ [620,650[ & 30 & 635 &12 \\ \hline \textbf{Total} & & & 200\\ \hline \end{array}\)

Table 5 : Idem Table 4 avec de plus amplitude des classes (seconde colonne), centre de classe (troisième colonne) et effectif.

 

\(\begin{array}{|c|ccc| } \hline \textbf{Classe} & \textbf{Amplitude} & \textbf{Centre} & \textbf{Effectif} \\ \hline [350,470[ & 90 & 410 &34 \\ [470,500[ & 30 & 485 &33 \\ [500,530[ & 30 & 515 &40\\ [530,560[ & 30 & 545 &35 \\ [560,590[ & 30 & 575 &30 \\ \mbox{plus que }590 & // & // &28 \\ \hline \textbf{Total} & & & 200\\ \hline \end{array}\)

Table 6 : Idem Table 5 mais avec choix de classes différent.

 

\(\begin{array}{|c|cc|c| } \hline \textbf{Classe} & \textbf{Centre} & \textbf{Effectif} & \textbf{Fréquence} \\ \hline [350,470[ & 410 &34 & 17\% \\ [470,500[ & 485 &33 & 16,5\% \\ [500,530[ & 515 &40 & 20 \% \\ [530,560[ & 545 &35 & 17,5\% \\ [560,590[ & 575 &30 & 15\% \\ \mbox{plus que }590 & // &28 & 14\% \\ \hline \textbf{Total}& & 200 & 100\% \\ \hline \end{array}\)

Table 7 : Table des loyers avec effectifs et fréquences (exprimées en pourcentage).

 

Pour autant que cela ait un sens (donc pour des variables quantitatives ou des variables qualitatives ordinales mais pas pour des variables qualitatives nominales) il peut s'avérer utile de considérer les fréquences cumulées.

On a que \(n_icc\) est le nombre d'individus pour lesquels \(X\) est inférieur ou égal à \(y_i \) (ou bien \(X\) appartient aux classes \(C_1, C_2, \ldots, C_i \)):

\(n_1cc = n_1 \mbox{ et } n_icc = n_1+ n_2 + \ldots + n_i = \displaystyle \displaystyle\sum_{j=1}^in_j \mbox{ pour } 2 \le i \le M.\)

Evidemment, si la variable a \(M\) modalités alors on a \(n_Mcc = n\) .

La Définition précédente s'adapte aisément pour définir la fréquence cumulée croissante

\(f_1cc = f_1 \mbox{ et } f_icc = f_1+f_2+ \ldots + f_i = \displaystyle \displaystyle\sum_{j=1}^if_j \mbox{ pour } 2 \le i \le M,\)

ou encore

\(f_icc = \dfrac{n_icc}{n}. \)

Bien entendu \( f_Mcc = 1\).

Un exemple de calcul des effectifs et fréquences cumulés est donné aux Tables 8 et 9.

 

\(\begin{array}{|c|c|c|c|c|c| } \hline \textbf{Classe} & m_i & n_i & n_icc & f_i & f_icc \\ \hline [350,470[ & 410 &34 & 34 & 17\% & 17\% \\ [470,500[ & 485 &33 & 67 & 16,5\% & 33,5\% \\ [500,530[ & 515 &40 & 107 & 20 \% & 53,5\%\\ [530,560[ & 545 &35 & 142 & 17,5\% & 71\%\\ [560,590[ & 575 &30 & 172 & 15\% & 86\%\\ \mbox{plus que }590 & // &28 & 200 & 14\% & 100\% \\ \hline \textbf{Total}& // & 200 & // & 100\% & //\\ \hline \end{array}\)

Table 8 : Table des loyers avec effectifs et fréquences (exprimées en pourcentage) ainsi que effectifs et fréquences cumulés correspondants.

 

\(\begin{array}{|c|c|c|c|c|} \hline \mbox{Cote }y_i & n_i & n_icc & f_i & f_icc \\ \hline 0 & 88& 88& 14,3\%& 14,3\%\\ 1& 13& 101& 2,1\%& 16,4\%\\ 2& 55& 156& 8,9\%& 25,3\%\\ 3& 71& 227& 11,5\%& 36,8\%\\ 4& 72& 299& 11,7\%& 48,5\%\\ 5& 56& 355& 9,1\%& 57,5\%\\ 6& 44& 399& 7,1\%& 64,7\%\\ 7& 41& 440& 6,6\%& 71,3\%\\ 8& 34& 474& 5,5\%& 76,8\%\\ 9& 26& 500& 4,2\%& 81,0\%\\ 10& 43& 543& 7,0\%& 88,0\%\\ 11& 14& 557& 2,3\%& 90,3\%\\ 12& 18& 575& 2,9\%& 93,2\%\\ 13& 15& 590& 2,4\%& 95,6\%\\ 14& 5& 595& 0,8\%& 96,4\%\\ 15& 5& 600& 0,8\%& 97,2\%\\ 16& 7& 607& 1,1\%& 98,4\%\\ 17& 2& 609& 0,3\%& 98,7\%\\ 18& 4& 613& 0,6\%& 99,4\%\\ 19& 4& 617& 0,6\%& 100,0\%\\ 20& 0& 617& 0,0\%& 100,0\%\\ \hline \end{array}\)

Table 9 : Résultats (entre 0/20 et 20/20) en BA1 à un examen, avec effectifs, fréquences, effectifs cumulés et fréquences cumulées.

 

Remarque : On peut également adapter cette définition pour définir des effectifs et fréquences cumulées décroissants.

Représentations graphiques

Dans cette section nous présentons trois types majeurs de représentation graphique, à savoir : diagramme circulaire, diagramme en barres et diagramme en bâtons. Il existe de nombreuses autres formes de représentations graphiques : histogramme, diagramme des fréquences cumulées, etc. que nous n'aborderons pas ici.

(a) Diagramme circulaire

Le diagramme circulaire (aussi appelé diagramme en secteurs, en camembert ou pie-chart (de l'anglais, littéralement graphe de tarte)) consiste en la représentation de la distribution d'une variable dans un disque de façon à avoir une proportionnalité directe entre la surface relative occupée par une modalité et la fréquence de cette modalité dans la population.

Plus précisément, un diagramme circulaire est un graphique constitué d'un disque divisé en secteurs dont les angles au centre sont proportionnels aux effectifs selon la règle

\(\alpha_i = \dfrac{n_i}{n} \times 360^{\circ} = f_i \times 360^{\circ}\)

avec \(\alpha_i\) l'angle au centre de la \(i \)ème modalité. Remarquez que

\( \displaystyle \displaystyle\sum_{i=1}^M\alpha_i=360^{\circ}.\)

Un exemple est présenté à la Figure 1. Notez que ce type de représentation graphique est valable pour tout type de variable (qualitatives, quantitatives) mais ne sera interprétable qu'à condition que le nombre de modalités (ou de classes de modalités) soit petit.

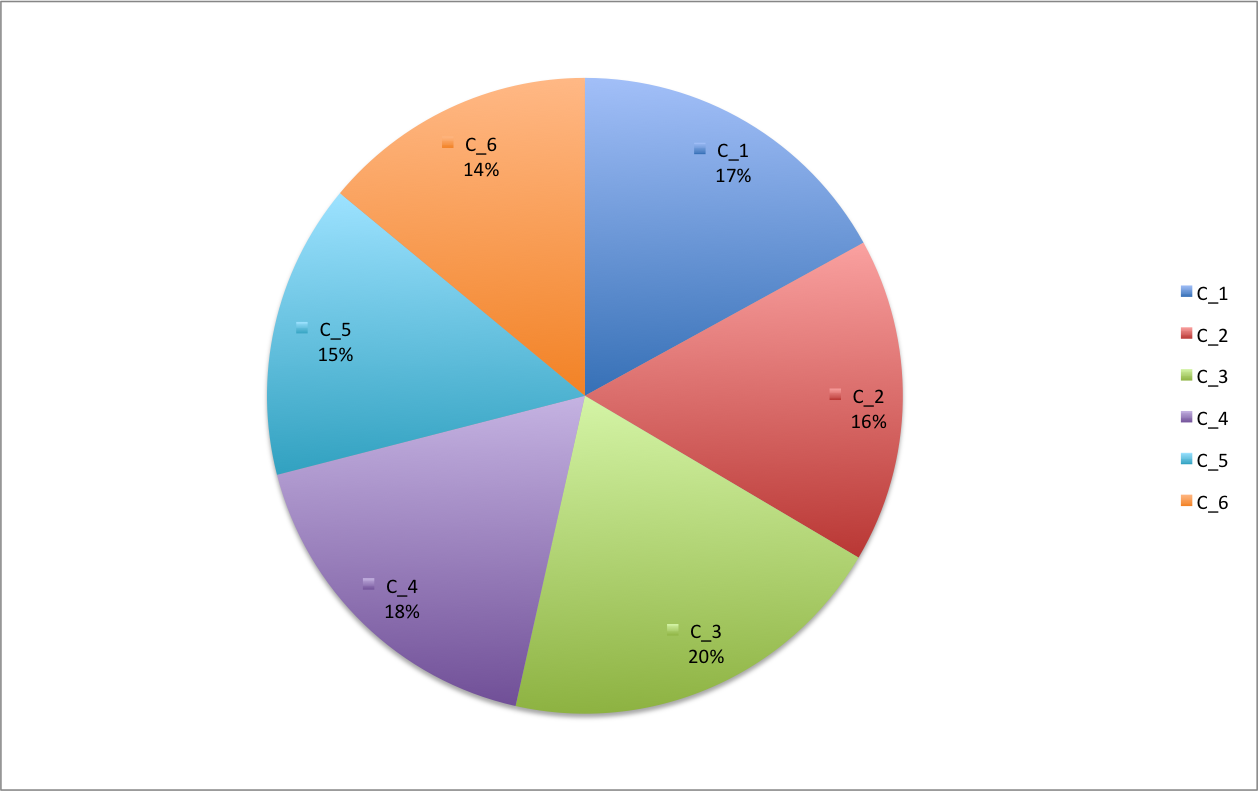
Figure 1 : Diagramme circulaire représentant la distribution des loyers étudiée dans la Table 8.

(b) Diagramme en barres

Dans le même ordre d'idées qu'à la section précédente, on peut préférer représenter la distribution des données à l'aide de rectangles horizontaux (ou verticaux) ayant tous une même base (de largeur arbitraire) et dont la hauteur est directement proportionnelle aux effectifs (ou, de façon équivalente, aux fréquences). On appelle ce type de graphique un diagramme en barres ou diagramme en tuyaux d'orgue.

Un exemple est présenté à la figure ci-dessous. Notez à nouveau que ce type de représentation graphique est valable pour tout type de variable (qualitatives, quantitatives) mais ne sera interprétable qu'à condition que le nombre de modalités (ou de classes de modalités) soit petit.

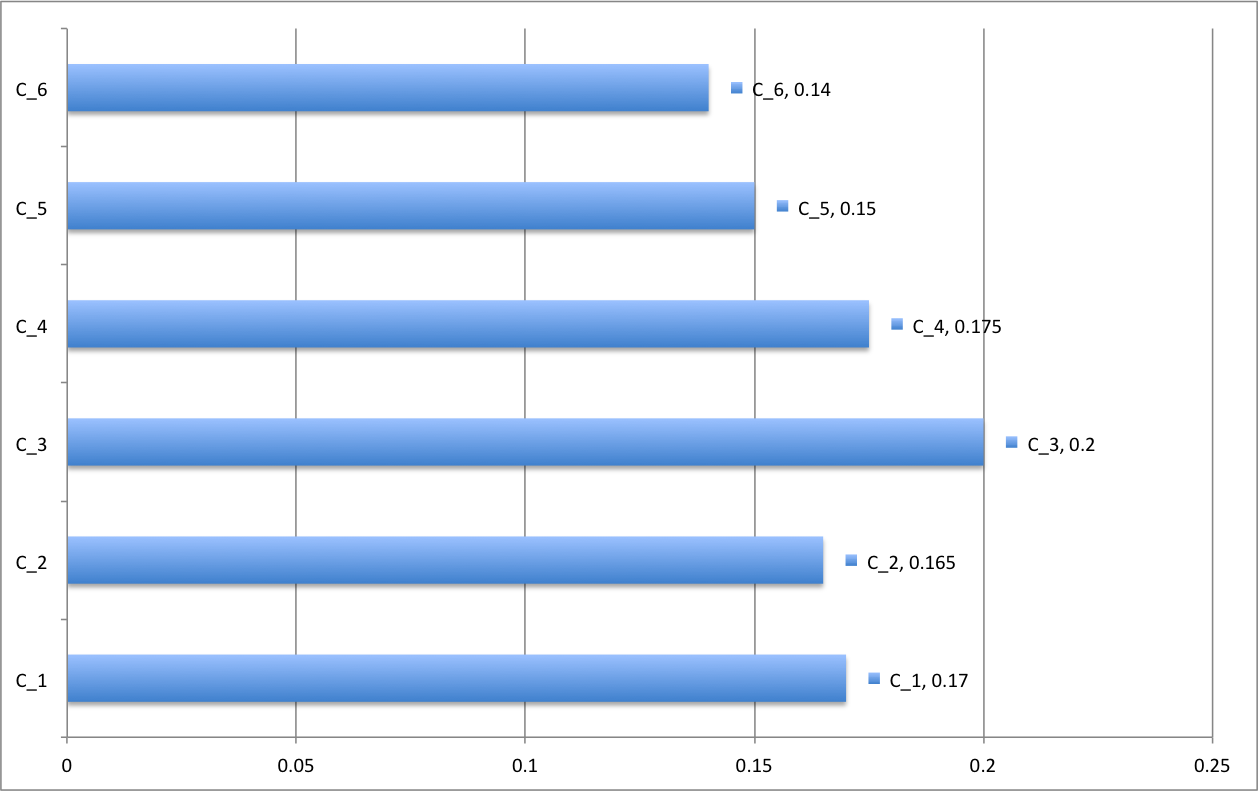
Figure 2 : Diagramme en barres de la distribution des loyers de la Table 8.

 

Remarque : Lorsque l'on traite une variable quantitative on appelera également ce type de graphique diagramme en bâtons, cf. Figure 3. Dans ce cas il est d'usage de représenter les bâtons verticalement, et de mettre en abscisse les valeurs de la variable en respectant l'ordre.

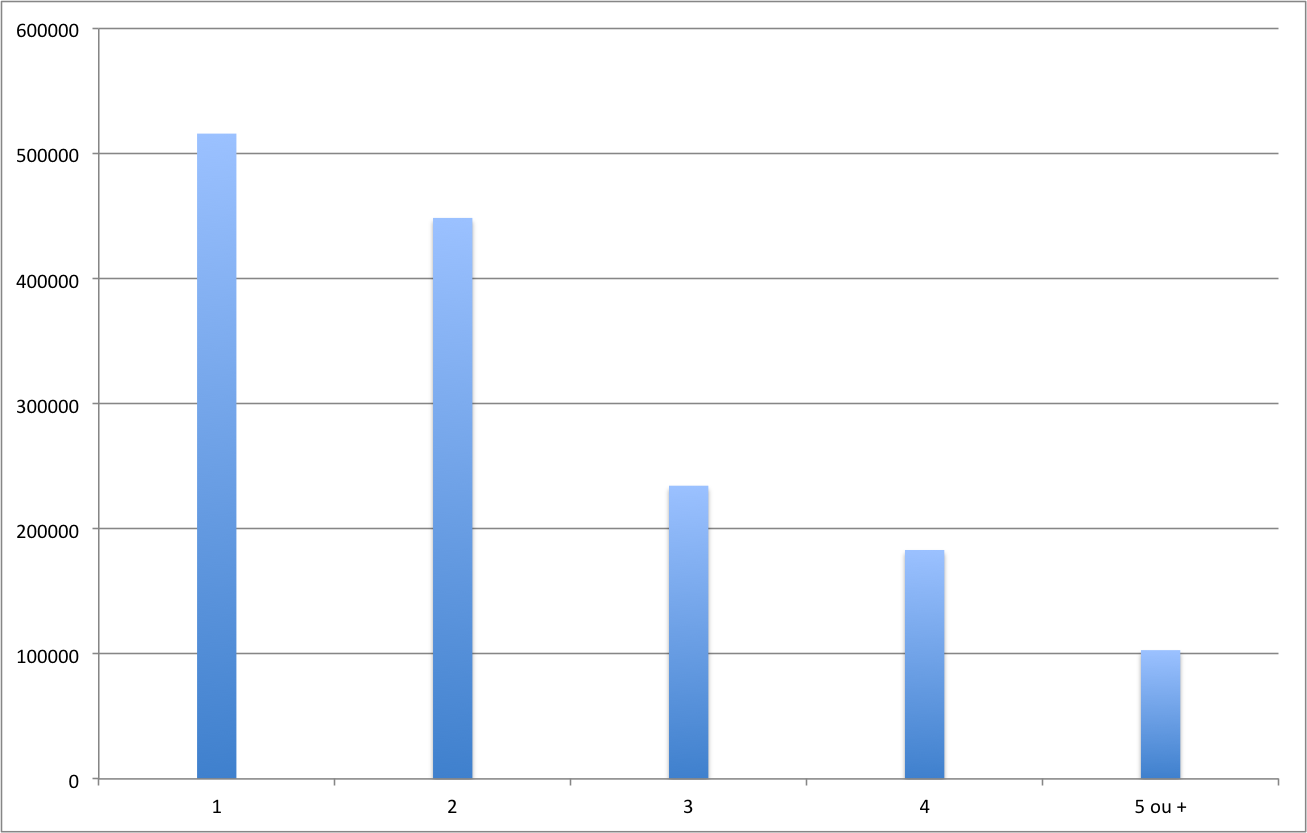
Figure 3 : Diagramme en bâtons de la distribution du nombre de personnes pas ménage en Wallonie au 1er janvier 2009 (source Direction générale Statistique et Information économique -- http://www.iweps.be/menages-prives-par-taille-en-wallonie-et-en-belgique).

Indicateurs numériques

L'ultime étape de toute description d'un jeu de données consiste en le calcul d'indicateurs numériques de "tendance"; ces indicateurs sont appelés statistiques.

(a) Indicateurs de position - moyenne, médiane et mode

Ces paramètres permettent de caractériser l'ordre de grandeur des observations. Ils servent comme indication de premier ordre sur la "tendance générale" du phénomène auquel on s'intéresse.

 

Par exemple, les données de la Table 10 représentent les résultats obtenus par 617 étudiants ayant passé un examen de BA1 dans une université belge en 2012.

 

Table 10 : Résultats obtenus par 617 étudiants à un examen; données brutes.

 

Ces données sont présentées après rangement dans la Table 11; la distribution (diagramme en bâtons) est représentée à la Figure 4.

 

\( \begin{array}{|c|c|c|c|c|} \hline \mbox{Cote } y_i & n_i & n_icc & f_i & f_icc \\ \hline 0 & 88& 88& 14,3\%& 14,3\%\\ 1& 13& 101& 2,1\%& 16,4\%\\ 2& 55& 156& 8,9\%& 25,3\%\\ 3& 71& 227& 11,5\%& 36,8\%\\ 4& 72& 299& 11,7\%& 48,5\%\\ 5& 56& 355& 9,1\%& 57,5\%\\ 6& 44& 399& 7,1\%& 64,7\%\\ 7& 41& 440& 6,6\%& 71,3\%\\ 8& 34& 474& 5,5\%& 76,8\%\\ 9& 26& 500& 4,2\%& 81,0\%\\ 10& 43& 543& 7,0\%& 88,0\%\\ 11& 14& 557& 2,3\%& 90,3\%\\ 12& 18& 575& 2,9\%& 93,2\%\\ 13& 15& 590& 2,4\%& 95,6\%\\ 14& 5& 595& 0,8\%& 96,4\%\\ 15& 5& 600& 0,8\%& 97,2\%\\ 16& 7& 607& 1,1\%& 98,4\%\\ 17& 2& 609& 0,3\%& 98,7\%\\ 18& 4& 613& 0,6\%& 99,4\%\\ 19& 4& 617& 0,6\%& 100,0\%\\ 20& 0& 617& 0,0\%& 100,0\%\\ \hline \end{array}\)

Table 11 : Résultats (entre 0/20 et 20/20) en BA1 à un examen, avec effectifs, fréquences,                    effectifs cumulés et fréquences cumulées.

 

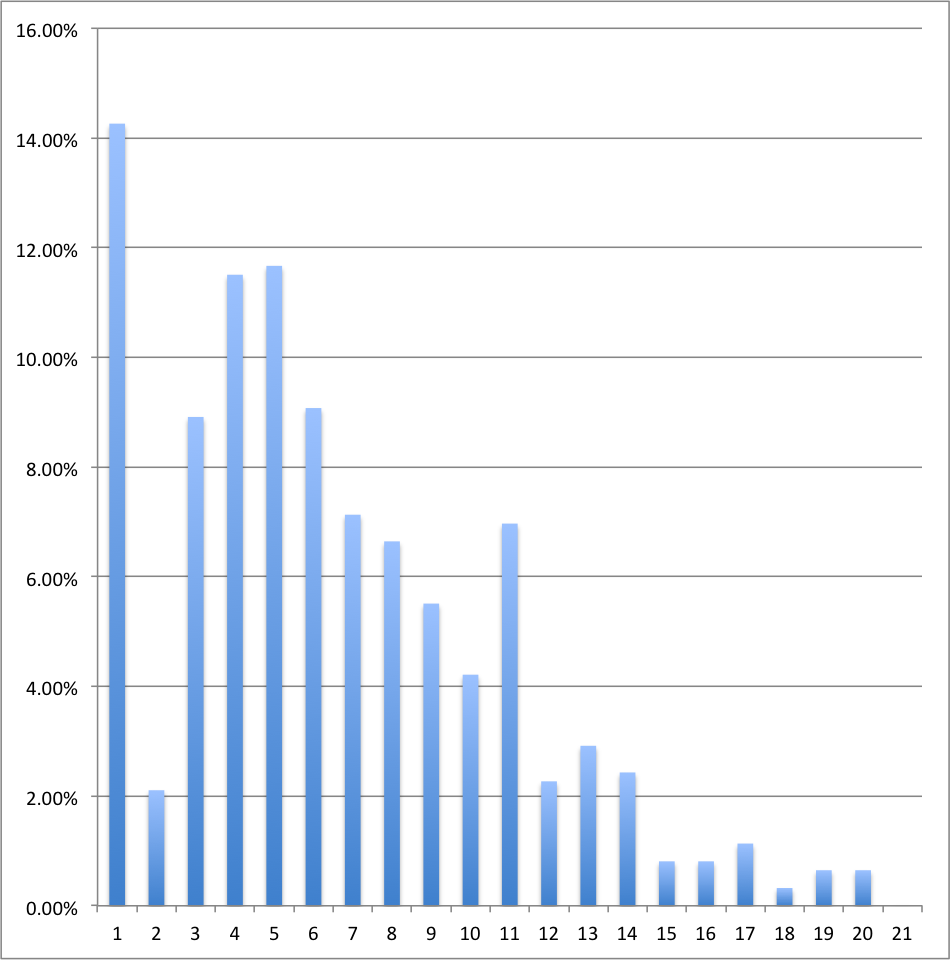
Figure 4 : Diagramme en bâtons des données de la Table 11.

 

On calcule la cote moyenne

\(\begin{array}{rcl} \bar{x} & =& \dfrac{1}{617} \left( 5+1+9+\ldots + 5+4+2 \right)\\ & =& \dfrac{1}{617} \left( 88\times0 + 13 \times 1 + \ldots + 4 \times 19 + 0 \times 20 \right) \\ & =& \displaystyle\sum_{i=1}^{20}y_if_i \\ & =& 5,5. \end{array}\)

 

Considérons les données de la Table 1. On calcule le prix moyen de location

\(\bar{x} = \dfrac{1}{200} \left( 350+370+375 + \ldots + 635+630\right) = 518,48\$ .\)

Si l'on ne dispose pas des données brutes mais seulement des données groupées en classe de la Table 4 alors on calcule la moyenne en utilisant les centres de classe

\(\bar{x} = \dfrac{1}{200}\left( 365\times 3 + \ldots + 635 \times 12\right) = 523,25\$.\)

La différence entre les deux valeurs est due à la perte d'informations entre le passage de la Table 1 à la Table 4.

La médiane est donc le "centre" de la population classée par ordre croissant. 

Par exemple, considérons l'échantillon classé \(\left\{ 1, 3, 5, 7, 9\right\} \). La médiane est la valeur centrale, soit \(x_{med} = 5 \).

Il n'y a parfois pas de valeur pour laquelle les fréquences cumulées atteignent exactement \(50\%\). Dans ce cas on a deux possibilités pour calculer la médiane.

1. Lorsqu'on dispose du jeu de \(n\) données brutes, on les range par ordre croissant \( x_1 \le x_2 \le \ldots \le x_n\) et  

• si \(n\) est impair alors \(x_{med}=x_{(n-1)/2+1}\) est la médiane de la population;
• si \(n\) est pair alors \(x_{med} = \frac{x_{n/2}+x_{n/2+1}}{2}\) est une médiane de la population.

2. Lorsque la distribution de l'échantillon est connue on appelle médiane la modalité (ou le centre de la classe) pour laquelle la fréquence cumulée dépasse \(50\%\) pour la première fois.

Par exemple, pour l'échantillon classé \(\left\{ 1, 3, 5, 7, 9, 20\right\} \), la médiane est la valeur centrale, soit \(x_{med} = (5+7)/2 = 6 \).  Pour l'échantillon classé \(\left\{ 1, 3, 5, 7, 93, 1250\right\} \), la médiane est la valeur centrale, soit \(x_{med} = (5+7)/2 = 6 \).

Si on reprend les données de la Table 11, la cote médiane se situe entre 4/20 et 5/20.

Pour les données de la Table 8, le loyer médian se situe quelque part dans la classe \([500, 530[ \). En reprenant les données brutes de la Table 1 on obtient que le loyer médian est de \(520\$\).

Par exemple, dans l'échantillon classé \(\left\{ 1, 3, 5, 7, 9, 20\right\}\) toutes les données apparaissant le même nombre de fois (une seule), elles sont toutes des modes.

Dans l'échantillon classé \(\left\{ 1, 1, 3, 5,5, 5, 7, 9, 20, 20\right\}\) la valeur \(5\) apparait trois fois et est donc la plus fréquente. Le mode de cet échantillon est donc \(x_{mod} = 5 \).

Dans l'échantillon classé \(\left\{ 1, 1,1, 3, 5,5, 5, 7, 9, 20, 20\right\}\) les valeurs \(1\) et \(5\) apparaissent trois fois toutes les deux. Elles sont toutes deux des modes pour cet échantillon : \(x_{mod} = \left\{ 1, 5 \right\} \).

Si on reprend les données de la Table 11, la cote la plus fréquente est 0/20. Le mode est donc \(x_{mod} = 0 \).

(b) Indicateurs de dispersion -- amplitude, variance et écart-type

Les indicateurs de position ne sont qu'une première approximation et ne résument (bien entendu) pas le jeu de données. 

Considérons un étudiant qui a une cote moyenne, sur 5 examens, de 8/20. Il pourrait avoir obtenu par exemple les résultats 0, 20, 12, 8, 0 ou bien les résultats 8, 8, 8, 8, 8.  Bien que possédant la même moyenne et la même médiane, les deux séries de cotes s'interprètent de façon totalement différente !

Une façon de capter (et par suite d'interpréter) le type de différence illustré à l'exemple ci-dessus consiste à étudier la dispersion de la population observée.

Si la variable a \(M\) modalités \(y_1, y_2, \ldots, y_M\) d'effectifs respectifs \(n_1, n_2, \ldots, n_M\) et de fréquences respectives \(f_1, f_2, \ldots, f_M\) alors on a les formules équivalentes

\(s^2 = \displaystyle\sum_{i=1}^M (y_i-\bar{x})^2 \frac{n_i}{n} = \sum_{i=1}^M(y_i-\bar{x})^2 f_i.\)

 Le théorème suivant permet de faciliter le calcul de la variance.

Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.

La variance étant obtenue en prenant le carré des observations, elle ne s'exprime pas dans les mêmes unités que la population. Pour l'interprétation, on utilisera donc l'écart-type.

Par exemple, dans l'échantillon \(\left\{ 1, 1, 1, 1, 1\right\}\) toutes les données sont égales : il n'y a pas de variabilité et \(s^2 = s = 0 \).

Dans l'échantillon \(\left\{ 1, 3, 5, 7, 9, 20\right\} \), la moyenne est \(7,5\). La variance est donc

\(\begin{array}{rcl} s^2 &=& \dfrac{ (1-7,5)^2+ (3-7,5)^2+(5-7,5)^2+(7-7,5)^2+(9-7,5)^2+(20-7,5)^2 }{6}\\ & =& \dfrac{1^2+3^2+5^2+7^2+9^2+20^2}{6}-(7,5)^2\\ & = &37,91. \end{array}\)

Prenant la racine carrée de ce nombre on obtient l'écart-type \(s=6,15 \).

Reprenons le jeu de données de la Table 11. Rappelons-nous que la cote moyenne sur cet échantillon est de 5,5. Par facilité de calcul on rajoute dans la table une colonne contenant le carré des différences entre les modalités et la moyenne (cf. Table 12). Prenant la moyenne de cette dernière colonne, on obtient une variance de 17,75 et un écart-type de 4,21.

\(\begin{array}{|c|c|c|c|c|c|} \hline \mbox{Cote }y_i & n_i & n_icc & f_i & f_icc & (y_i-\bar{x})^2 \\ \hline 0 & 88& 88& 14,3\%& 14,3\% & 30,27\\ 1& 13& 101& 2,1\%& 16,4\% & 20,27 \\ 2& 55& 156& 8,9\%& 25,3\% & 12,26 \\ 3& 71& 227& 11,5\%& 36,8\% & 6,26 \\ 4& 72& 299& 11,7\%& 48,5\% & 2,25 \\ 5& 56& 355& 9,1\%& 57,5\% & 0,25\\ 6& 44& 399& 7,1\%& 64,7\% & 0,24\\ 7& 41& 440& 6,6\%& 71,3\% & 2,242\\ 8& 34& 474& 5,5\%& 76,8\% & 6,23\\ 9& 26& 500& 4,2\%& 81,0\% & 12,23\\ 10& 43& 543& 7,0\%& 88,0\% & 20,22\\ 11& 14& 557& 2,3\%& 90,3\% & 30,22\\ 12& 18& 575& 2,9\%& 93,2\% & 42,21\\ 13& 15& 590& 2,4\%& 95,6\% & 56,21\\ 14& 5& 595& 0,8\%& 96,4\% & 72,20\\ 15& 5& 600& 0,8\%& 97,2\% & 90,20\\ 16& 7& 607& 1,1\%& 98,4\% & 110,19\\ 17& 2& 609& 0,3\%& 98,7\% & 132,19\\ 18& 4& 613& 0,6\%& 99,4\% & 156,18\\ 19& 4& 617& 0,6\%& 100,0\% & 182,18\\ 20& 0& 617& 0,0\%& 100,0\% & 210,17\\ \hline \end{array}\)

Table 12 : Résultats (entre 0/20 et 20/20) en BA1 à un examen, avec effectifs, fréquences, effectifs cumulés et fréquences cumulées et une colonne contenant les carrés de différences entre valeurs et moyenne.

 

Exemples détaillés

1. Donner un exemple d'une variable quantitative ayant 12 modalités.

Solution détaillée : La variable mois de naissance, dont les modalités varient entre 1 (janvier) et 12 (décembre).

 

2. Donner un exemple d'une variable qualitative nominale.

 Solution détaillée : La variable "diplôme".

 

3. Quelle est la moyenne arithmétique de l'échantillon \(\left\{ 1, 3, 2, 1, 4 \right\}\)?

Solution détaillée : On calcule

\(\dfrac{1+3+2+1+4}{5} = \dfrac{11}{5} = 2,2.\)

 

4. Quelle est la moyenne arithmétique de l'échantillon \(\left\{ 5, 12, -2, 5, 3, 8 \right\}\) ?

Solution détaillée : On calcule

\(\dfrac{5+12-2+5+3+8}{6} = \dfrac{31}{6} = 5,166...\)

 

5. On prend 50 mesures d'une certaine quantité, et on obtient le tableau suivant :

   \(\begin{array}{|c|c|} \hline \mbox{Modalité} & \mbox{Effectif}\\ \hline 4 & 5\\ 7 & 12\\ 8 & 9 \\ 10 & 13 \\ 14 & 11 \\ \hline \end{array}\)

   Quelle est la moyenne arithmétique de cet échantillon?

Solution détaillée : On calcule

\( \dfrac{4\times 5+7\times 12+8\times 9+10\times 13+14\times 11}{50}= 9,2.\)

 

6. On prend 80 mesures d'une certaine quantité, et on obtient le tableau suivant :

   \(\begin{array}{|c|c|} \hline \mbox{Modalité} & \mbox{Effectif}\\ \hline [300, 320[ & 14\\ [320, 370[ & 23\\ [370, 410[ & 31 \\ [410, 500[ & 12 \\ \hline \end{array}\)

   Calculer le centre de chacune des classes et utiliser ces centres de classes pour donner une approximation de la moyenne arithmétique de cet échantillon.

 Solution détaillée : On complète le tableau avec les centres de classes

\(\begin{array}{|c|c|c|} \hline \mbox{Modalité} & \mbox{Centre} & \mbox{Effectif}\\ \hline [300, 320[ & 310 & 14\\ [320, 370[ & 345 & 23\\ [370, 410[ & 390 & 31 \\ [410, 500[ & 455 & 12 \\ \hline \end{array}\)

et on calcule

\(\dfrac{310\times 14+ \ldots + 455\times 12}{80} = 372,81.\)

 

7. Quelle est la médiane de l'échantillon \(\left\{ 5, 12, -2, 5, 3 \right\}\) ?

Solution détaillée : On range les données par ordre croissant

-2, 3, 5, 5, 12

et on déduit que la médiane est 5.

 

8. Quelle est la médiane de l'échantillon \(\left\{ 1, 4, 2, 9, 3, 6, 12, 1, 4, 2 \right\}\) ?

Solution détaillée : On range les données par ordre croissant

1,1, 2, 2, 3, 4, 4, 6, 9, 12

et on déduit que la médiane est (3+4)/2= 3,5 .

 

9.  Quels sont la variance et l'écart-type de l'échantillon \(\left\{ 1, 4, 2, 9, 3\right\} \)?

Solution détaillée : On calcule la moyenne

\(\dfrac{1+4+2+9+3}{5} = \dfrac{19}{5} = 3,8\)

et donc la variance est

\(s^2 = \dfrac{1^2+4^2+2^2+9^2+3^2}{5} - (3,8)^2 = 7,76.\)

On prend la racine carrée pour déduire l'écart-type \(s = \sqrt{7,76}=2,78\).

 

10. Quel est l'amplitude de l'échantillon \(\left\{ 1, 4, 2, 9, 3\right\} \)?

 Solution détaillée : On range les données par ordre croissant

1,2, 3, 4, 9

et on déduit que l'amplitude est 9-1 = 8 .

 

11. Quel est le mode de l'échantillon \(\left\{ -2, 3, 1, 4, -3, 5, 1 \right\}\) ?

 Solution détaillée : On établit une table d'effectifs

\(\begin{array}{|c|c|} \hline \mbox{Modalité} & \mbox{effectif}\\ \hline -3 & 1\\ -2 & 1\\ 1 & 2\\ 3 & 1\\ 4 & 1\\ 5 & 1\\ \hline \end{array}\)

Toutes les modalités ont la même fréquence excepté "\(1\)" qui apparaît deux fois. Donc le mode est \(1\).

 

12. Donner un exemple d'échantillon de taille 5 ayant une moyenne égale à 4.

 Solution détaillée : Il nous faut 5 valeurs \(x_1, x_2, x_3, x_4, x_5\) satisfaisant

\(\dfrac{1}{5} \displaystyle \displaystyle\sum_{i=1}^5x_i = 4.\)

Ceci revient à trouver 5 nombres tels que

\(\displaystyle \displaystyle\sum_{i=1}^5x_i = 20.\)

En réfléchissant un peu on déduit que l'échantillon \(\left\{4, 4, 4, 4, 4\right\}\) est un exemple trivial. D'autres exemples moins triviaux sont simples à construire :

• un échantillon symétrique autour de \(4\) : \(\left\{2, 3, 4, 5, 6\right\}\)
• un échantillon symétrique autour de \(4\) : \(\left\{0, 2, 4, 6, 8\right\}\)
• l'échantillon \(\left\{0, 0, 0, 0, 20\right\}\)

De manière générale on prend n'importe quelles valeurs pour \(x_1, x_2,x_3, x_4\) et \(x_5 = 20 - \displaystyle \displaystyle \displaystyle\sum_{i=1}^4x_i \).

 

13. Donner un échantillon de taille 5 contenant l'élément \(0\) et ayant une moyenne égale à 4.

 Solution détaillée : Il nous faut 5 valeurs \(x_1, x_2, x_3, x_4, x_5\) satisfaisant

\(\dfrac{1}{5} \displaystyle \displaystyle\sum_{i=1}^5x_i = 4\)

avec \(x_1=0\) (cela ne change rien de décider que c'est \(x_1\) et pas un des autres qui vaut \(0\)). Ceci revient à trouver 4 nombres tels que

\(\displaystyle \displaystyle\sum_{i=2}^5x_i = 20.\)

En réfléchissant un peu on déduit que l'échantillon \(\left\{0, 5, 5, 5, 5\right\} \)est un exemple trivial. D'autres exemples moins triviaux sont simples à construire.

L'échantillon \(\left\{0, 3, 4, 5, 8\right\}\) satisfait les contraintes imposées.

De manière générale on prend n'importe quelles valeurs pour \(x_2, x_3, x_4\) et \(x_5 = 20 - \displaystyle \displaystyle \displaystyle\sum_{i=2}^4x_i \).

 

14. Donner deux exemples d'échantillons différents ayant la même moyenne et le même écart-type.

Solution détaillée : Il est aisé de construire deux échantillons de même moyenne. Pour que les écart-types soient les mêmes, il faut s'arranger pour que les deux échantillons aient la même dispersion. Par exemple on peut prendre

\(\left\{18, 18\right\} \mbox{et } \left\{18, 18, 18, 18\right\}\)

mais il s'agit d'un exemple trivial. Les échantillons

\(\left\{1, 3, 5\right\} \mbox{et } \left\{1, 3, 3, 5\right\}\)

sont un exemple un peu moins idiot. Beaucoup d'autres exemples sont possibles.

 

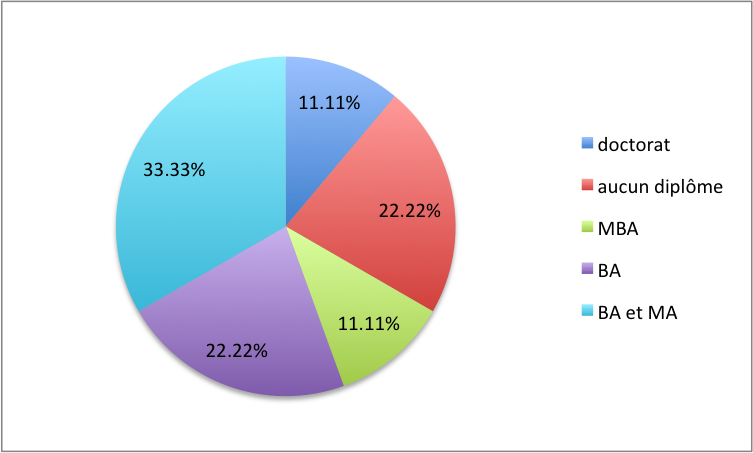
15. Sur les 108 chefs d'entreprise interrogés, 12 avaient obtenu un doctorat, 24 n'avaient aucun diplôme, 12 avaient un MBA, 24 avaient un BA et 36 avaient à la fois un BA et un MA. Représenter le diagramme circulaire de ce jeu de données.

 Solution détaillée : On établit d'abord une table d'effectifs et de fréquences.

\(\begin{array}{|c|c|c|} \hline \mbox{Modalité} & \mbox{effectif} & \mbox{fréquence}\\ \hline \mbox{doctorat} & 12 & 12/108 = 11,11 \% \\ \mbox{aucun} & 24 & 24 /108 = 22,22 \% \\ \mbox{MBA} & 12 & 12/108 = 11,11 \% \\ \mbox{BA} & 24 & 24/108 = 22, 22 \% \\ \mbox{BA + MA} &36 & 36/108 = 33,33 \% \\ \hline \end{array}\)

En appliquant la règle de proportionnalité, on déduit le diagramme suivant.

 

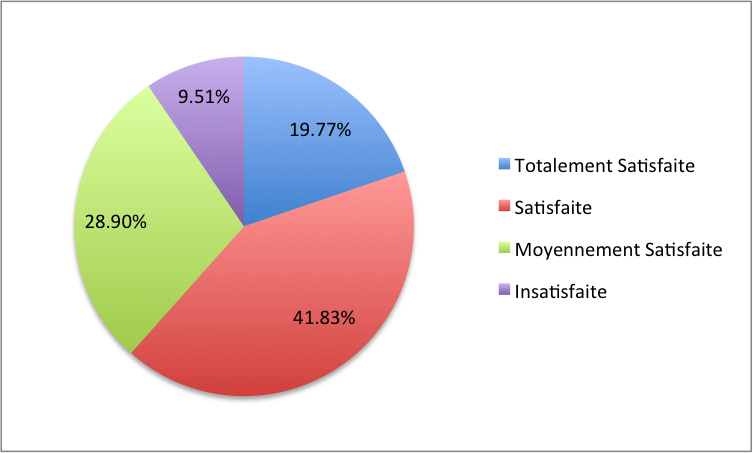
16. Sur les 263 personnes interrogées après avoir séjourné à l'hôtel B, 52 se disaient totalement satisfaites de leur expérience, 110 se disaient satisfaites, 76 se disaient moyennement satisfaites et le reste se disait insatisfait.

    Calculer la distribution et représenter le diagramme circulaire de ce jeu de données. Sur une échelle de 1 à 4 (1 représentant la satisfaction totale, 4 représentant l'insatisfaction), donner une évaluation de la satisfaction moyenne des 263 personnes.

Solution détaillée : On établit d'abord une table d'effectifs et de fréquences.

\(\begin{array}{|c|c|c|} \hline \mbox{Modalité} & \mbox{effectif} & \mbox{fréquence}\\ \hline 1 & 52 & 52/263 = 19,77 \% \\ 2 & 110 & 110/263 = 41,83 \% \\ 3 & 76 & 76/263 = 28,90 \% \\ 4 & 25 & 25/263 = 9,51 \% \\ \hline \end{array}\)

En appliquant la règle de proportionnalité, on déduit le diagramme suivant.

On calcule le score moyen

\(9,51\% \times 1 + 41,83\%\times 2+28,9\%\times 3+19,77\%\times 4 = 2,28.\)

 

17. Voici les résultats obtenus par des étudiants à un examen :

    6, 7, 0, 1, 11, 9, 12, 6, 7, 9, 19, 8, 7, 0, 9, 14, 3, 8, 0, 16, 16, 2, 0, 7, 0, 10, 9, 13, 4, 0, 0, 8, 8, 6, 13, 7, 0, 10, 2, 0, 6, 0, 9, 5, 15, 1, 4, 14, 6, 20

    1. Ranger ce jeu de données en déterminant les effectifs et les fréquences des différentes modalités de la variable "cote" (entre 0 et 20/20).
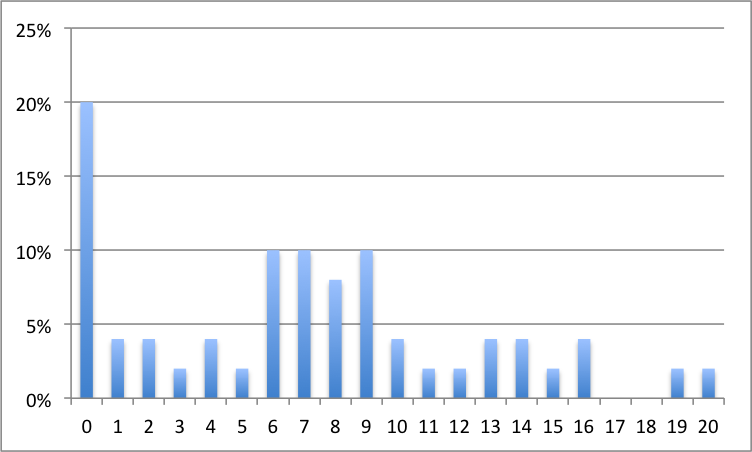
    2. Donner le diagramme de fréquence (diagramme en bâtons) des résultats.
    3. Calculer la cote moyenne à cet examen (exprimer votre réponse jusqu'à la deuxième décimale, sans arrondir).
    4. Calculer la variance et l'écart-type des résultats (exprimer votre réponse jusqu'à la deuxième décimale, sans arrondir).
    5. Calculer la note moyenne si on ne tient pas compte des cotes nulles.
    6. Parmi les étudiants qui ont réussi l'examen avec une cote supérieure ou égale à 12 quel pourcentage a obtenu une note strictement supérieure à 15 ?

 Solution détaillée : Il y a \(50\) cotes, donc \(n=50\).

1. On obtient le tableau suivant

\(\begin{array}{|c|c|c|c|} \hline \mbox{Cote} & n_i & f_i & f_icc \\ \hline 0 & 10& 20\%& 20\%\\ 1& 2& 4\%& 24\%\\ 2& 2& 4\%& 28\%\\ 3& 1& 2\%& 30\%\\ 4& 2& 4\%& 34\%\\ 5& 1& 2\%& 36\%\\ 6& 5& 10\%& 46\%\\ 7& 5& 10\%& 56\%\\ 8& 4& 8\%& 64\%\\ 9& 5& 10\%& 74\%\\ 10& 2& 4\%& 78\%\\ 11& 1& 2\%& 80\%\\ 12& 1& 2\%& 82\%\\ 13& 2& 4\%& 86\%\\ 14& 2& 4\%& 90\%\\ 15& 1& 2\%& 92\%\\ 16& 2& 4\%& 96\%\\ 17& 0& 0\%& 96\%\\ 18& 0& 0\%& 96\%\\ 19& 1& 2\%& 98\%\\ 20& 1& 2\%& 100\%\\ \hline \end{array} \)

Les effectifs sont donnés dans la deuxième colonne et les fréquences dans la troisième colonne.

2. On construit le diagramme suivant.

3. On calcule la moyenne des 50 cotes

\(\bar{x} = \dfrac{0\times 10+1\times 2+2\times 2+\ldots+19\times 1+20\times 1}{50}= 6,94.\)

 

4. La variance est donnée par

\(\begin{array}{rcl} s^2 & =& \left( \dfrac{0^2\times 10+1^2\times 2+2^2\times 2+ \ldots+19^2\times 1+ 20^2\times 1}{50}\right) - ( 6,94)^2 \\ & = &28,53 \end{array}\)

et l'écart-type est \(s=5,37 \).

5. En excluant les notes égales à 0 on travaille sur un échantillon de taille 40; on a donc le tableau suivant.

\(\begin{array}{|c|c|c|c|} \hline \mbox{Cote} & n_i & f_i \\ \hline 1& 2& 5\%\\ 2& 2& 5\%\\ 3& 1& 2,5\%\\ 4& 2& 5\%\\ 5& 1& 2,5\%\\ 6& 5& 12,5\%\\ 7& 5& 12,5\%\\ 8& 4& 10\%\\ 9& 5& 12,5\%\\ 10& 2& 5\%\\ 11& 1& 2,5\%\\ 12& 1& 2,5\%\\ 13& 2& 5\%\\ 14& 2& 5\%\\ 15& 1& 2,5\%\\ 16& 2& 5\%\\ 17& 0& 0\%\\ 18& 0& 0\%\\ 19& 1& 2,5\%\\ 20& 1& 2,5\%\\ \hline \end{array}\)

dont on déduit la moyenne

\(\bar{x} = \dfrac{1\times 2+2\times 2+ \ldots + 19\times 1+20\times 1}{40} = 8,675.\)

 

6. 10 étudiants ont obtenu une note supérieure ou égale à 12, parmi lesquels 4 ont une note strictement supérieure à 15; donc la proportion demandée est

\(\dfrac{4}{10} = 40 \%.\)

 

18. Pour quelle valeur de \(x\) l'échantillon \(\left\{ 1, 3, 2, 1, x\right\}\) a-t-il une moyenne égale à 4 ?

 Solution détaillée : Il faut résoudre

\(\dfrac{1+ 3+ 2+ 1+ x}{5} = 4\)

dont on déduit \(x = 13 \).

 

19. La moyenne obtenue par l'étudiant L. sur les trois premiers examens passés est de 12/20. Quelle cote doit-il obtenir à son examen suivant afin d'avoir une moyenne (sur les 4 examens) égale à 13/20 ?

 Solution détaillée : Il faut résoudre

\(\dfrac{3\times 12+ x}{4} = 13\)

dont on déduit \(x = 16 \).

 

20. Si la moyenne arithmétique des nombres \(28, x , 42, 78\) et \(104\) est \(62\), quelle est la moyenne arithmétique des nombres \(112, 28, 42\) et \(x\) ?

Solution détaillée : On sait

\(\dfrac{28+ x+ 42+ 78+ 104}{5} = 62\)

dont on déduit \(x = 58\) et donc

\(\dfrac{ 112 + 28 +42 + x}{4} = \dfrac{ 112 + 28 +42 + 58}{4} = 60.\)

Preuves