Auto-Math

Université catholique de Louvain - UCL

Théorie du module : Statistiques descriptives

Exemples détaillés

  1. Donner un exemple d'une variable quantitative ayant 12 modalités.

Solution détaillée : La variable mois de naissance, dont les modalités varient entre 1 (janvier) et 12 (décembre).

 

  1. Donner un exemple d'une variable qualitative nominale.

 Solution détaillée : La variable "diplôme".

 

  1. Quelle est la moyenne arithmétique de l'échantillon \(\left\{ 1, 3, 2, 1, 4 \right\}\)?

Solution détaillée : On calcule

\(\dfrac{1+3+2+1+4}{5} = \dfrac{11}{5} = 2,2.\)

 

  1. Quelle est la moyenne arithmétique de l'échantillon \(\left\{ 5, 12, -2, 5, 3, 8 \right\}\) ?

Solution détaillée : On calcule

\(\dfrac{5+12-2+5+3+8}{6} = \dfrac{31}{6} = 5,166...\)

 

  1. On prend 50 mesures d'une certaine quantité, et on obtient le tableau suivant :

    \(\begin{array}{|c|c|} \hline \mbox{Modalité} & \mbox{Effectif}\\ \hline 4 & 5\\ 7 & 12\\ 8 & 9 \\ 10 & 13 \\ 14 & 11 \\ \hline \end{array}\)

    Quelle est la moyenne arithmétique de cet échantillon?

Solution détaillée : On calcule

\( \dfrac{4\times 5+7\times 12+8\times 9+10\times 13+14\times 11}{50}= 9,2.\)

 

  1. On prend 80 mesures d'une certaine quantité, et on obtient le tableau suivant :

    \(\begin{array}{|c|c|} \hline \mbox{Modalité} & \mbox{Effectif}\\ \hline [300, 320[ & 14\\ [320, 370[ & 23\\ [370, 410[ & 31 \\ [410, 500[ & 12 \\ \hline \end{array}\)

    Calculer le centre de chacune des classes et utiliser ces centres de classes pour donner une approximation de la moyenne arithmétique de cet échantillon.

 Solution détaillée : On complète le tableau avec les centres de classes

\(\begin{array}{|c|c|c|} \hline \mbox{Modalité} & \mbox{Centre} & \mbox{Effectif}\\ \hline [300, 320[ & 310 & 14\\ [320, 370[ & 345 & 23\\ [370, 410[ & 390 & 31 \\ [410, 500[ & 455 & 12 \\ \hline \end{array}\)

et on calcule

\(\dfrac{310\times 14+ \ldots + 455\times 12}{80} = 372,81.\)

 

  1. Quelle est la médiane de l'échantillon \(\left\{ 5, 12, -2, 5, 3 \right\}\) ?

Solution détaillée : On range les données par ordre croissant

-2, 3, 5, 5, 12

et on déduit que la médiane est 5.

 

  1. Quelle est la médiane de l'échantillon \(\left\{ 1, 4, 2, 9, 3, 6, 12, 1, 4, 2 \right\}\) ?

Solution détaillée : On range les données par ordre croissant

1,1, 2, 2, 3, 4, 4, 6, 9, 12

et on déduit que la médiane est (3+4)/2= 3,5 .

 

  1.  Quels sont la variance et l'écart-type de l'échantillon \(\left\{ 1, 4, 2, 9, 3\right\} \)?

Solution détaillée : On calcule la moyenne

\(\dfrac{1+4+2+9+3}{5} = \dfrac{19}{5} = 3,8\)

et donc la variance est

\(s^2 = \dfrac{1^2+4^2+2^2+9^2+3^2}{5} - (3,8)^2 = 7,76.\)

On prend la racine carrée pour déduire l'écart-type \(s = \sqrt{7,76}=2,78\).

 

  1. Quel est l'amplitude de l'échantillon \(\left\{ 1, 4, 2, 9, 3\right\} \)?

 Solution détaillée : On range les données par ordre croissant

1,2, 3, 4, 9

et on déduit que l'amplitude est 9-1 = 8 .

 

  1. Quel est le mode de l'échantillon \(\left\{ -2, 3, 1, 4, -3, 5, 1 \right\}\) ?

 Solution détaillée : On établit une table d'effectifs

\(\begin{array}{|c|c|} \hline \mbox{Modalité} & \mbox{effectif}\\ \hline -3 & 1\\ -2 & 1\\ 1 & 2\\ 3 & 1\\ 4 & 1\\ 5 & 1\\ \hline \end{array}\)

Toutes les modalités ont la même fréquence excepté "\(1\)" qui apparaît deux fois. Donc le mode est \(1\).

 

  1. Donner un exemple d'échantillon de taille 5 ayant une moyenne égale à 4.

 Solution détaillée : Il nous faut 5 valeurs \(x_1, x_2, x_3, x_4, x_5\) satisfaisant

\(\dfrac{1}{5} \displaystyle \displaystyle\sum_{i=1}^5x_i = 4.\)

Ceci revient à trouver 5 nombres tels que

\(\displaystyle \displaystyle\sum_{i=1}^5x_i = 20.\)

En réfléchissant un peu on déduit que l'échantillon \(\left\{4, 4, 4, 4, 4\right\}\) est un exemple trivial. D'autres exemples moins triviaux sont simples à construire :

  • un échantillon symétrique autour de \(4\) : \(\left\{2, 3, 4, 5, 6\right\}\)
  • un échantillon symétrique autour de \(4\) : \(\left\{0, 2, 4, 6, 8\right\}\)
  • l'échantillon \(\left\{0, 0, 0, 0, 20\right\}\)

De manière générale on prend n'importe quelles valeurs pour \(x_1, x_2,x_3, x_4\) et \(x_5 = 20 - \displaystyle \displaystyle \displaystyle\sum_{i=1}^4x_i \).

 

  1. Donner un échantillon de taille 5 contenant l'élément \(0\) et ayant une moyenne égale à 4.

 Solution détaillée : Il nous faut 5 valeurs \(x_1, x_2, x_3, x_4, x_5\) satisfaisant

\(\dfrac{1}{5} \displaystyle \displaystyle\sum_{i=1}^5x_i = 4\)

avec \(x_1=0\) (cela ne change rien de décider que c'est \(x_1\) et pas un des autres qui vaut \(0\)). Ceci revient à trouver 4 nombres tels que

\(\displaystyle \displaystyle\sum_{i=2}^5x_i = 20.\)

En réfléchissant un peu on déduit que l'échantillon \(\left\{0, 5, 5, 5, 5\right\} \)est un exemple trivial. D'autres exemples moins triviaux sont simples à construire.

L'échantillon \(\left\{0, 3, 4, 5, 8\right\}\) satisfait les contraintes imposées.

De manière générale on prend n'importe quelles valeurs pour \(x_2, x_3, x_4\) et \(x_5 = 20 - \displaystyle \displaystyle \displaystyle\sum_{i=2}^4x_i \).

 

  1. Donner deux exemples d'échantillons différents ayant la même moyenne et le même écart-type.

Solution détaillée : Il est aisé de construire deux échantillons de même moyenne. Pour que les écart-types soient les mêmes, il faut s'arranger pour que les deux échantillons aient la même dispersion. Par exemple on peut prendre

\(\left\{18, 18\right\} \mbox{et } \left\{18, 18, 18, 18\right\}\)

mais il s'agit d'un exemple trivial. Les échantillons

\(\left\{1, 3, 5\right\} \mbox{et } \left\{1, 3, 3, 5\right\}\)

sont un exemple un peu moins idiot. Beaucoup d'autres exemples sont possibles.

 

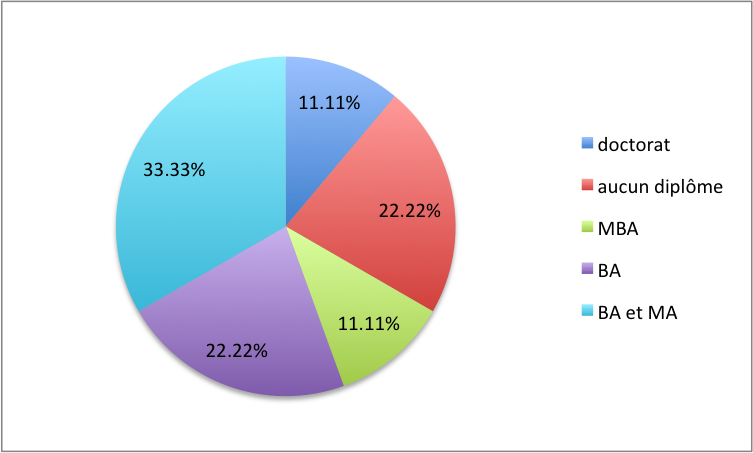
  1. Sur les 108 chefs d'entreprise interrogés, 12 avaient obtenu un doctorat, 24 n'avaient aucun diplôme, 12 avaient un MBA, 24 avaient un BA et 36 avaient à la fois un BA et un MA. Représenter le diagramme circulaire de ce jeu de données.

 Solution détaillée : On établit d'abord une table d'effectifs et de fréquences.

\(\begin{array}{|c|c|c|} \hline \mbox{Modalité} & \mbox{effectif} & \mbox{fréquence}\\ \hline \mbox{doctorat} & 12 & 12/108 = 11,11 \% \\ \mbox{aucun} & 24 & 24 /108 = 22,22 \% \\ \mbox{MBA} & 12 & 12/108 = 11,11 \% \\ \mbox{BA} & 24 & 24/108 = 22, 22 \% \\ \mbox{BA + MA} &36 & 36/108 = 33,33 \% \\ \hline \end{array}\)

En appliquant la règle de proportionnalité, on déduit le diagramme suivant.

 

  1. Sur les 263 personnes interrogées après avoir séjourné à l'hôtel B, 52 se disaient totalement satisfaites de leur expérience, 110 se disaient satisfaites, 76 se disaient moyennement satisfaites et le reste se disait insatisfait.

    Calculer la distribution et représenter le diagramme circulaire de ce jeu de données. Sur une échelle de 1 à 4 (1 représentant la satisfaction totale, 4 représentant l'insatisfaction), donner une évaluation de la satisfaction moyenne des 263 personnes.

Solution détaillée : On établit d'abord une table d'effectifs et de fréquences.

\(\begin{array}{|c|c|c|} \hline \mbox{Modalité} & \mbox{effectif} & \mbox{fréquence}\\ \hline 1 & 52 & 52/263 = 19,77 \% \\ 2 & 110 & 110/263 = 41,83 \% \\ 3 & 76 & 76/263 = 28,90 \% \\ 4 & 25 & 25/263 = 9,51 \% \\ \hline \end{array}\)

En appliquant la règle de proportionnalité, on déduit le diagramme suivant.

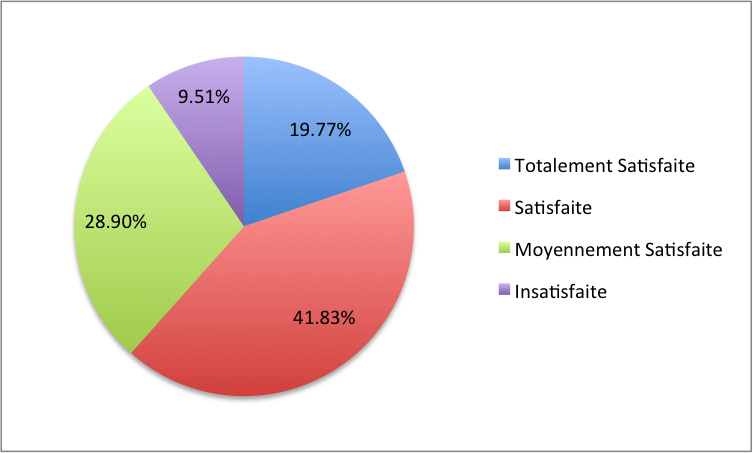
On calcule le score moyen

\(9,51\% \times 1 + 41,83\%\times 2+28,9\%\times 3+19,77\%\times 4 = 2,28.\)

 

  1. Voici les résultats obtenus par des étudiants à un examen :

    6, 7, 0, 1, 11, 9, 12, 6, 7, 9, 19, 8, 7, 0, 9, 14, 3, 8, 0, 16, 16, 2, 0, 7, 0, 10, 9, 13, 4, 0, 0, 8, 8, 6, 13, 7, 0, 10, 2, 0, 6, 0, 9, 5, 15, 1, 4, 14, 6, 20

    1. Ranger ce jeu de données en déterminant les effectifs et les fréquences des différentes modalités de la variable "cote" (entre 0 et 20/20).
    2. Donner le diagramme de fréquence (diagramme en bâtons) des résultats.
    3. Calculer la cote moyenne à cet examen (exprimer votre réponse jusqu'à la deuxième décimale, sans arrondir).
    4. Calculer la variance et l'écart-type des résultats (exprimer votre réponse jusqu'à la deuxième décimale, sans arrondir).
    5. Calculer la note moyenne si on ne tient pas compte des cotes nulles.
    6. Parmi les étudiants qui ont réussi l'examen avec une cote supérieure ou égale à 12 quel pourcentage a obtenu une note strictement supérieure à 15 ?

 Solution détaillée : Il y a \(50\) cotes, donc \(n=50\).

  1. On obtient le tableau suivant

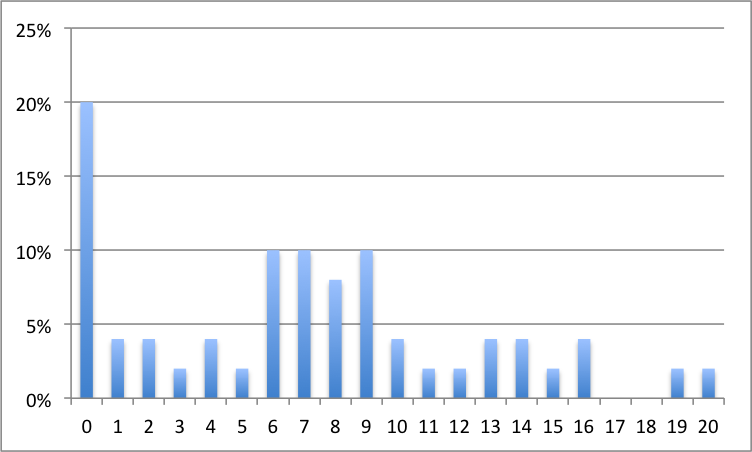
\(\begin{array}{|c|c|c|c|} \hline \mbox{Cote} & n_i & f_i & f_icc \\ \hline 0 & 10& 20\%& 20\%\\ 1& 2& 4\%& 24\%\\ 2& 2& 4\%& 28\%\\ 3& 1& 2\%& 30\%\\ 4& 2& 4\%& 34\%\\ 5& 1& 2\%& 36\%\\ 6& 5& 10\%& 46\%\\ 7& 5& 10\%& 56\%\\ 8& 4& 8\%& 64\%\\ 9& 5& 10\%& 74\%\\ 10& 2& 4\%& 78\%\\ 11& 1& 2\%& 80\%\\ 12& 1& 2\%& 82\%\\ 13& 2& 4\%& 86\%\\ 14& 2& 4\%& 90\%\\ 15& 1& 2\%& 92\%\\ 16& 2& 4\%& 96\%\\ 17& 0& 0\%& 96\%\\ 18& 0& 0\%& 96\%\\ 19& 1& 2\%& 98\%\\ 20& 1& 2\%& 100\%\\ \hline \end{array} \)

Les effectifs sont donnés dans la deuxième colonne et les fréquences dans la troisième colonne.

  1. On construit le diagramme suivant.

  1. On calcule la moyenne des 50 cotes

\(\bar{x} = \dfrac{0\times 10+1\times 2+2\times 2+\ldots+19\times 1+20\times 1}{50}= 6,94.\)

 

  1. La variance est donnée par

\(\begin{array}{rcl} s^2 & =& \left( \dfrac{0^2\times 10+1^2\times 2+2^2\times 2+ \ldots+19^2\times 1+ 20^2\times 1}{50}\right) - ( 6,94)^2 \\ & = &28,53 \end{array}\)

et l'écart-type est \(s=5,37 \).

  1. En excluant les notes égales à 0 on travaille sur un échantillon de taille 40; on a donc le tableau suivant.

\(\begin{array}{|c|c|c|c|} \hline \mbox{Cote} & n_i & f_i \\ \hline 1& 2& 5\%\\ 2& 2& 5\%\\ 3& 1& 2,5\%\\ 4& 2& 5\%\\ 5& 1& 2,5\%\\ 6& 5& 12,5\%\\ 7& 5& 12,5\%\\ 8& 4& 10\%\\ 9& 5& 12,5\%\\ 10& 2& 5\%\\ 11& 1& 2,5\%\\ 12& 1& 2,5\%\\ 13& 2& 5\%\\ 14& 2& 5\%\\ 15& 1& 2,5\%\\ 16& 2& 5\%\\ 17& 0& 0\%\\ 18& 0& 0\%\\ 19& 1& 2,5\%\\ 20& 1& 2,5\%\\ \hline \end{array}\)

dont on déduit la moyenne

\(\bar{x} = \dfrac{1\times 2+2\times 2+ \ldots + 19\times 1+20\times 1}{40} = 8,675.\)

 

  1. 10 étudiants ont obtenu une note supérieure ou égale à 12, parmi lesquels 4 ont une note strictement supérieure à 15; donc la proportion demandée est

\(\dfrac{4}{10} = 40 \%.\)

 

  1. Pour quelle valeur de \(x\) l'échantillon \(\left\{ 1, 3, 2, 1, x\right\}\) a-t-il une moyenne égale à 4 ?

 Solution détaillée : Il faut résoudre

\(\dfrac{1+ 3+ 2+ 1+ x}{5} = 4\)

dont on déduit \(x = 13 \).

 

  1. La moyenne obtenue par l'étudiant L. sur les trois premiers examens passés est de 12/20. Quelle cote doit-il obtenir à son examen suivant afin d'avoir une moyenne (sur les 4 examens) égale à 13/20 ?

 Solution détaillée : Il faut résoudre

\(\dfrac{3\times 12+ x}{4} = 13\)

dont on déduit \(x = 16 \).

 

  1. Si la moyenne arithmétique des nombres \(28, x , 42, 78\) et \(104\) est \(62\), quelle est la moyenne arithmétique des nombres \(112, 28, 42\) et \(x\) ?

Solution détaillée : On sait

\(\dfrac{28+ x+ 42+ 78+ 104}{5} = 62\)

dont on déduit \(x = 58\) et donc

\(\dfrac{ 112 + 28 +42 + x}{4} = \dfrac{ 112 + 28 +42 + 58}{4} = 60.\)

Théorie

Retour au module