Théorie du module : Repères et vecteurs
Table des matières
- Le plan \(\mathbb{R}^2\)
- L'espace \(\mathbb{R}^3\)
- La notion de vecteur
- Opérations sur les vecteurs
- Vecteurs et points particuliers
- Exemples détaillés
Le plan \(\mathbb{R}^2\)
(a) Repère
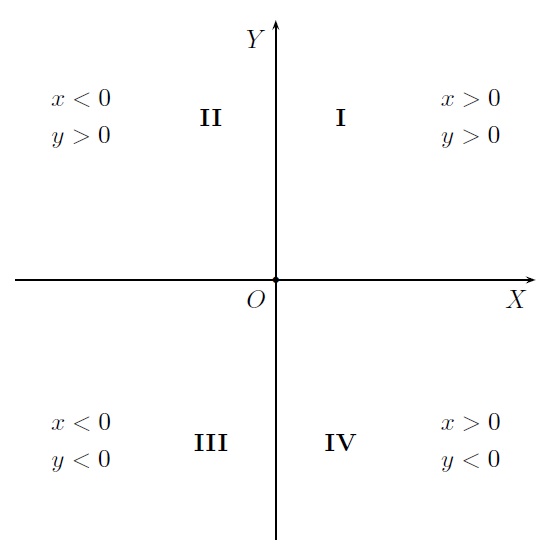
De même que l'on a identifié les points de la droite réelle (munie d'un repère : une origine et une longueur unité) aux nombres réels, on peut identifier les points du plan aux couples de nombres réels. Pour cela, il convient de se donner dans le plan un repère, constitué de deux droites sécantes, chacune munie d'une unité de longueur et qui se coupent en leur point origine. L'une des droites est appelée l'axe des \(x\)ou axe des abscisses, noté \(OX\), et l'autre est l'axe des \(y\)ou axe des ordonnées, noté \(OY\). En général, on utilise deux droites perpendiculaires, munies de la même unité de longueur. On parle alors de repère cartésien orthonormé. Le plan est ainsi divisé en quatre quadrants, le premier d'entre eux étant délimité par la partie positive des deux axes.
(b) Coordonnées cartésiennes
D'un point \(P\) quelconque du plan, on mène des parallèles aux axes qui coupent ceux-ci en \(a\) pour l'axe des \(x\) et en \(b\) pour l'axe des \(y\). Le point \(P\) est ainsi associé au couple de nombres réels \((a,b)\). Inversément, à tout couple de nombres réels \((a,b)\), en menant des parallèles aux axes passant par \(a\) porté sur l'axe des \(x\) et par \(b\) porté sur l'axe des \(y\), on fait correspondre l'unique point d'intersection de ces deux droites. Le couple \((a,b)\) est appelé coordonnées cartésiennes du point \(P\). Le nombre \(a\) est l'abscisse de \(P\) et le nombre \(b\) est son ordonnée.
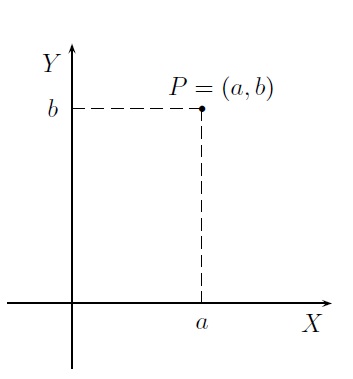
(c) Notion de distance
\(d(P,Q)= \sqrt{(x_q -x_p)^2 + (y_q-y_p)^2}.\)
Cette formule est une application immédiate du Théorème de Pythagore au triangle rectangle \(PQR\).
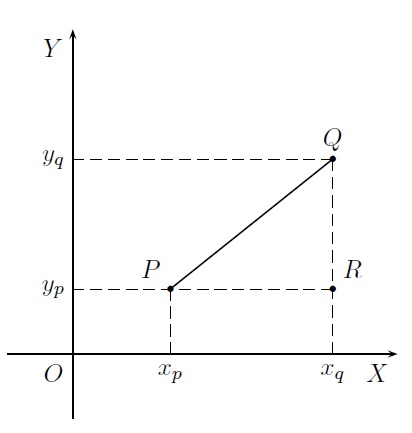
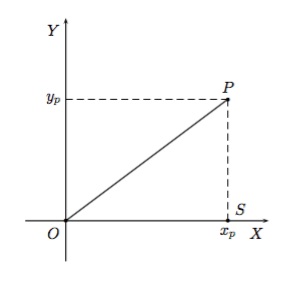
En particulier, la distance d'un point \(P=(x_p,y_p)\) à l'origine est donnée par \(\sqrt {x_p^2 +y_p^2}\) qui est la longueur de l'hypoténuse du triangle rectangle \(OPS\).
Application : Equation du cercle
Dans un plan fixé, on se donne un point \(C\) et un nombre \(r>0\).
\(d(P,C)=r.\)
Pour établir l'équation cartésienne du cercle, on se place dans un repère. Les coordonnées du point \(C\) dans ce repère sont \((x_c,y_c)\). Soit \(P=(x,y)\), un point du cercle. Puisque \(d(P,C)=r\), on a
\(\sqrt{(x-x_c)^2+(y-y_c)^2}=r.\)
\((x-x_c)^2+(y-y_c)^2=r^2.\)
En particulier, l'équation du cercle centré en \((0,0)\) et de rayon \(r\)} est\(x^2+y^2=r^2.\)
(d) Coordonnées polaires
Pour préciser la position d'un point \(P\), au lieu de ses coordonnées cartésiennes \((x,y)\), on peut donner les informations suivantes :
- la distance de \(P\) à l'origine, notée \(r\) (\(r>0\)),
- l'angle entre l'axe \(OX\) et \(OP\), noté \(\theta \). Par convention, \(\theta\in [0,2\pi[\, \).
Ce sont les coordonnées polaires du point \(P\).
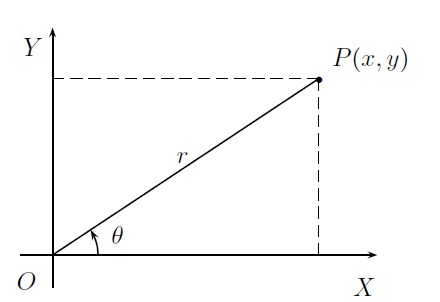
On observe immédiatement que
\(\left\{ \begin{array}{l} x = r \cos \theta\\ y = r \sin \theta \end{array}\right.\)
Le lien dans l'autre sens demande un peu plus d'attention. Vu que \(r\) est la distance de \(P\) à l'origine, on a
\(r =\sqrt{x^2 + y^2 }.\)
Pour \(\theta\), on note que si \(x = 0\) alors \(\theta = \frac{\pi}{2}\) ou \(\frac{3\pi}{2}\), selon que \(y > 0\) ou \(y < 0\). Si \(x \neq 0\), on a
\(\tan\theta=\frac{y}{x},\)
ce qui nous permet de trouver \(\theta\), en y ajoutant au besoin \(\pi\) selon les signes de \(x\) et \(y\).
Par exemple, pour \(P = (- \frac{\sqrt{3}}{2}, -\frac{1}{2})\) on trouve
\(r=\sqrt{\frac{3}{4}+\frac{1}{4}}=1\)
et
\(\arctan \frac{y}{x} = \arctan \frac{\sqrt{3}}{3} = \frac{\pi}{6}\)
et on doit prendre \(\theta = \frac{\pi}{6} + \pi=\frac{7\pi}{6}\) car les coordonnés cartésiennes de \(P\) sont toutes les deux négatives.
L'intérêt des coordonnées polaires est qu'elles permettent de décrire certaines figures géométriques à l'aide d'équations particulièrement simples. Voici quelques exemples :
Le cercle de centre \(O\) et de rayon \(R\) sera décrit par l'équation \(r = R\).
Une demi-droite issue de \(O\) et formant un angle \(\alpha\) avec l'axe \(OX\) sera décrite par \(\theta = \alpha\).
L'équation d'une ellipse en coordonnées polaires est
\(r = \frac{a - c^2/a }{1 + e \cos \theta}. \)
Cette description est utilisée en astronomie car la terre (ou une autre planète) décrit une ellipse dont un foyer est occupé par le soleil.
L'équation de la feuille de trèfle est donnée par \(r = \cos 3\theta \).
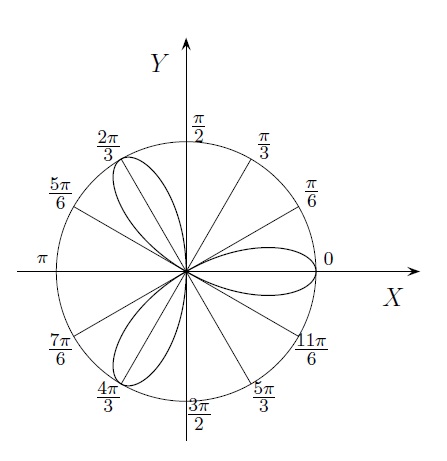
Si on essayait d'obtenir l'équation cartésienne correspondante, on pourrait utiliser le fait que \(\cos 3 \theta = \cos 2 \theta \cos \theta - \sin 2 \theta \sin \theta = \cos^3 \theta - 3 \sin^2\theta \cos \theta\) et en tirer la relation
\(r^4 = r^3\cos^3 \theta - 3 (r^2 \sin^2 \theta)(r\cos \theta)\)
ou encore
\((x^2 + y^2 )^2 = x^3 - 3x y^2.\)
Il n'est pas évident de voir l'allure de la courbe à partir de cette équation ! En coordonnées polaires, les choses sont plus simples.
L'espace \(\mathbb{R}^3\)
(a) Repère
Dans les sections précédentes, nous avons travaillé dans le plan. Si l'on veut travailler dans l'espace à trois dimensions, il faut considérer 3 axes. Un repère dans l'espace est constitué de trois droites sécantes, chacune munie d'une unité de longueur, et qui se coupent en leur point origine. Ces trois doites sont l'axe des \(x\), l'axe des \(y\) et l'axe des \(z\). Lorsque les trois droites dont perpendiculaires deux à deux et munies de la même unité de longueur, on parle de repère cartésien orthonormé. En général, les axes des \(y\) et des \(z\) se trouvent dans le plan de la feuille et celui des \(x\) se projette vers l'avant.
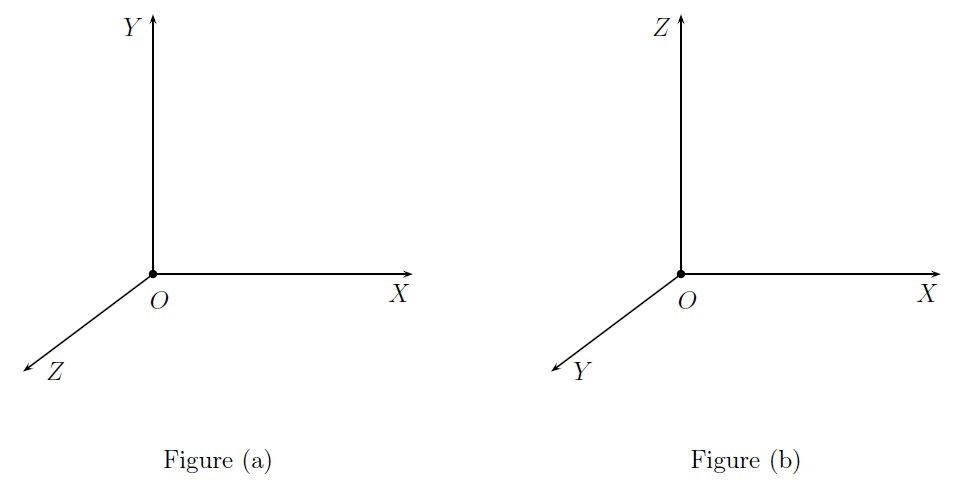
Ainsi placés, ces 3 axes déterminent un système de coordonnées droit ou d'orientation directe. On dit que le repère formé par les axes \(OX\), \(OY\) et \(OZ\) est d'orientation directe si un spectateur "debout" sur le plan \(OXY\), les pieds en \(O\) et la tête en \(Z\), observe que pour amener la droite \(OX\) sur la droite \(OY\), il doit faire une rotation dans le sens antihorlogique (on regarde le plus petit angle possible). Dans le cas contraire, le repère est dit d'orientation rétrograde.
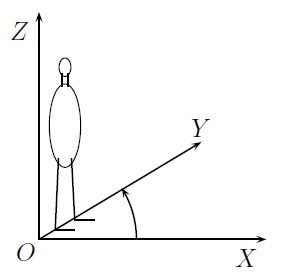
Remarque : Notons que pour savoir si un repère est direct ou rétrograde, l'ordre dans lequel on place les axes est important. Si on permute 2 axes, on change l'orientation du repère. On la change aussi quand on change la direction des axes. Par exemple le repère de la Figure (a) est d'orientation directe tandis que le repère de la Figure (b) est d'orientation rétrograde.
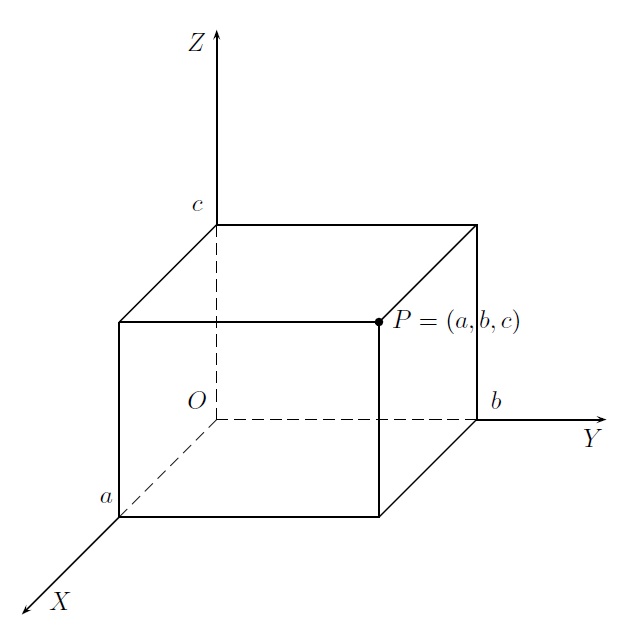
(b) Coordonnées cartésiennes
D'un point \(P\) quelconque de l'espace, on mène des parallèles aux axes qui coupent ceux-ci en \(a\) pour l'axe des \(x\), en \(b\) pour l'axe des \(y\) et en \(c\) pour l'axe des \(z\). Le point \(P\) est ainsi associé au triple de nombres réels \((a,b,c)\) qui sont les coordonnées cartésiennes du point \(P\).
(c) Notion de distance
\(d(P,Q)= \sqrt{(x_q -x_p)^2 + (y_q-y_p)^2+(z_q-z_p)^2}.\)
Cette formule provient d'une double application du Théorème de Pythagore. Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
En particulier, la distance d'un point \(P=(x_p,y_p,z_p)\) à l'origine est donnée par \(\sqrt {x_p^2 +y_p^2+z_p^2}\).
Application : Equation de la sphère
Dans l'espace, on se donne un point \(C\) et un nombre \(r>0\).
\(d(P,C)=r.\)
Pour établir l'équation cartésienne de la sphère, on se place dans un repère. Les coordonnées du point \(C\) dans ce repère sont \((x_c,y_c,z_c)\). Soit \(P=(x,y,z)\), un point de la sphère. Puisque \(d(P,C)=r\), on a
\(\sqrt{(x-x_c)^2+(y-y_c)^2+(z-z_c)^2}=r.\)
\((x-x_c)^2+(y-y_c)^2+(z-z_c)^2=r^2.\)
En particulier, l'équation de la sphère centré en \((0,0,0)\) et de rayon \(r\) est\(x^2+y^2+z^2=r^2.\)
(d) Coordonnées cylindriques
Pour obtenir les coordonnées cylindriques, on garde une des coordonnées cartésiennes, par exemple \(z\), et, dans le plan de coordonnées correspondant aux 2 autres on passe aux coordonnées polaires. Un point \(P\) se trouvera ainsi repéré par
- la cote \(z\),
- les coordonnées polaires \(r\) et \(\theta\) de sa projection orthogonale dans le plan \(OXY\).
Ce type de coordonnées est indiqué pour une surface dont les coupes horizontales sont des cercles centrés sur l'axe \(OZ\). Voici quelques exemples :
Un cylindre circulaire droit d'axe \(OZ\) et de rayon \(R\) sera décrit par l'équation \(r = R\).
Une surface de révolution engendrée par la rotation autour de \(OZ\) du graphe d'une fonction \(f : I \rightarrow \mathbb{R}^+ \); \(z \rightarrow f(z)\) sera décrite par \(r = f(z)\) simplement. Par exemple, le paraboloïde \(z = \frac{x^2 }{a^2 } + \frac{y^2}{a^2}\) sera décrit par \(r = a \sqrt{z}\).
Ces coordonnées sont souvent utilisées en physique pour l'étude de mouvements de rotation par exemple.
(e) Coordonnées sphériques
Pour préciser la position d'un point sur la surface terrestre, on donne la longitude et la latitude. Les coordonnées sphériques vont dans ce sens.
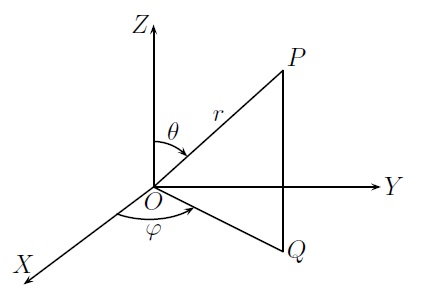
Pour préciser la position d'un point \(P\) dans l'espace, on peut donner les trois quantités suivantes :
- la distance du point \(P\) à l'origine, notée \(r\) (\(r>0\)),
- l'angle que fait le demi-plan comprenant \(OZ\) et \(P\) avec le demi-plan \(OXZ\), appelé longitude et noté \(\varphi\),
- l'angle que fait \(OP\) avec \(OZ\), appelé co-latitude et noté \(\theta\) (la latitude se compte à partir de l'équateur).
Le lien avec les coordonnées cartésiennes est donné par les équations
\(\left\{ \begin{array}{l} x = r \sin \theta \cos \varphi\\ y = r \sin \theta \sin \varphi\\ z = r \cos \theta \end{array} \right.\)
Voici quelques exemples :
La sphère de centre \(O\) et de rayon \(R\) est décrite par l'équation \(r = R\).
Un demi-plan issu de \(OZ\) sera décrit par \(\varphi = \alpha\) (\(\alpha\) donné).
Un cône de révolution d'axe \(OZ\) sera décrit par \(\theta = \alpha\) (\(\alpha\) donné).
La notion de vecteur
Nous présentons cette notion dans le plan (\(\mathbb{R}^2\)) et dans l'espace \((\mathbb{R}^3)\). Des quantités comme l'aire, le volume, la longueur, la température et le temps n'ont qu'une intensité et peuvent être entièrement représentées par un nombre réel (accompagné de l'unité de mesure adéquate). Une grandeur de ce type est une grandeur scalaire et le nombre correspondant est un scalaire. Des concepts tels que la vitesse ou la force ont à la fois une intensité, un sens et une direction. En physique, on appelle vecteur une quantité caractérisée par une longueur (ou intensité ou grandeur), par une direction et par un sens dans cette direction. Citons comme illustrations, l'effet d'un champ magnétique dans l'espace avec son intensité et sa direction; l'effet d'une force appliquée en un point caractérisée par une intensité et une direction; un avion qui se déplace avec une certaine vitesse dans une certaine direction ; un déplacement dans le plan caractérisé par une longueur ou distance et une direction.
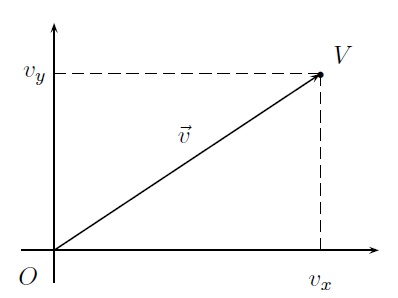
Supposons que l'on déplace un objet d'une position \(A\) à une position \(B\). On peut représenter ce déplacement par un segment fléché, la pointe de la flèche étant placée au point \(B\) et l'origine en \(A\), pour indiquer que le mouvement s'est effectué de \(A\) vers \(B\). On utilise alors \(\overrightarrow{AB}\) comme notation pour le vecteur. Il est important de réaliser qu'un vecteur est entièrement caractérisé par sa longueur et sa direction. L'endroit où l'on place dans le plan, ou dans l'espace, l'origine d'un vecteur est sans importance, seules comptent sa longueur et sa direction.
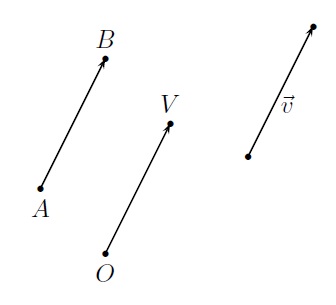
Dans la figure ci-dessus, \(\overrightarrow{AB}\) et \(\overrightarrow{OV}\) définissent le même vecteur que l'on pourrait représenter par le symbole \(\vec{v}\). En d'autres termes, un vecteur est défini indépendamment de la position où on le place dans le plan ou dans l'espace. Mathématiquement, tous les segments fléchés de même longueur et de même direction sont équivalents (on dit qu'ils forment une classe d'équivalence) et peuvent être représentés par n'importe lequel d'entre eux.
(a) Vecteurs du plan \(\mathbb{R}^2\)
Considérons un repère cartésien orthonormé. En plaçant l'origine du vecteur \(\vec{v}\) à l'origine du repère, on obtient le point \(V\) qui est l'extrémité de \(\vec{v}\). On a donc \(\vec{v}=\overrightarrow{OV}\). Le point \(V\) est un point du plan et a donc des coordonnées : \(V=(v_x,v_y)\). Les composantes du vecteur \(\vec{v}\) sont les coordonnées du point \(V\). On écrira \(\vec{v}=(v_x,v_y)\).
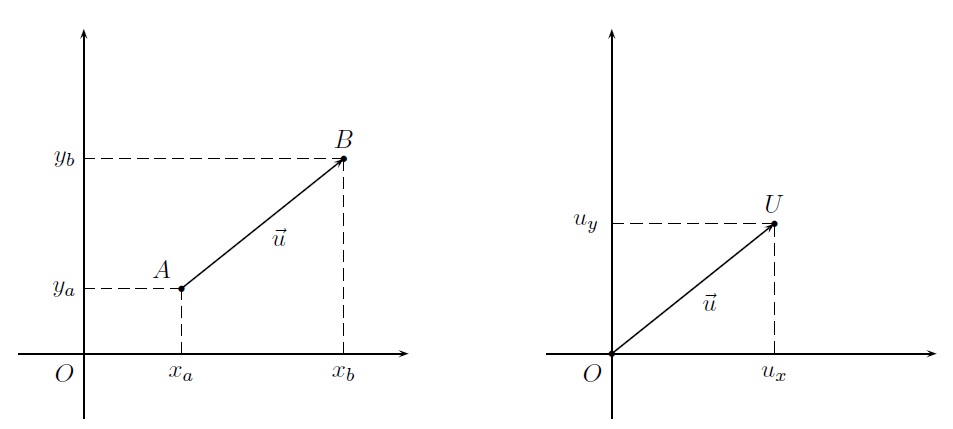
Si \((x_a,y_a)\) et \((x_b,y_b)\) sont respectivement les coordonnées des points \(A\) et \(B\), le vecteur \(\overrightarrow{AB}\) ou \(\vec{u}\) qu'ils définissent, a pour composantes \((u_x,u_y)=(x_b-x_a,y_b-y_a)\). En effet, le vecteur \(\overrightarrow{AB}\) peut être identifié au vecteur \(\overrightarrow{OU}\).
\(\|\vec{v}\| =\sqrt{v_x^2+v_y^2}.\)
Si \(\vec{u}=\overrightarrow{AB}=(x_b-x_a,y_b-y_a)\) alors\(\|\vec{u}\| =\|\overrightarrow{AB}\| =\sqrt{(x_b-x_a)^2+(y_b-y_a)^2}.\)
Il ne s'agit de rien d'autre que de l'application du Théorème de Pythagore.
Dans le plan, si un vecteur \(\vec{v}\) est connu par sa longueur \(\|\vec{v}\|\) et par l'angle \(\theta\) (mesuré dans le sens contraire des aiguilles d'une montre) qu'il forme avec l'axe horizontal, on en détermine aisément les composantes \((v_x,v_y)\) par
\(v_x=\|\vec{v}\|\cos\theta,\quad v_y=\|\vec{v}\|\sin\theta.\)
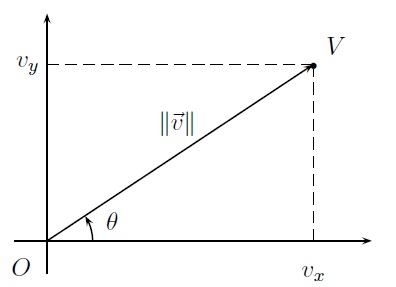
Inversément, on détermine la longueur \(\|\vec{v}\|\) d'un vecteur \(\vec{v}\), ainsi que l'angle \(\theta\) qu'il forme avec l'axe horizontal par
\(\|\vec{v}\|=\sqrt{v_x^2+v_y^2}, \quad \tan\theta=v_y/v_x,\)
pour \(v_x\neq 0\), ce qui nous permet de trouver \(\theta\), en y ajoutant au besoin \(\pi\) selon les signes de \(v_x\) et \(v_y\).
Pour plus de détails, vous pouvez consulter le chapitre de trigonométrie.
Par exemple, si le vent souffle à 12km/h dans la direction N\(40^\circ\)W, on peut exprimer sa vitesse par un vecteur \(\vec{v}\). La direction N\(40^\circ\)W correspond à un angle de \(130^\circ\). On a donc
\( \vec{v}= (v_x,v_y)= (\|\vec{v}\| \cos 130^\circ,\|\vec{v}\| \sin 130^\circ) = (-7,7; 9,2).\)
(b) Vecteurs de l'espace \(\mathbb{R}^3\)
Dans le cas de vecteurs dans l'espace, on parlera de triplets ordonnés de nombres réels. Par exemple, le vecteur \(\vec{v}=\overrightarrow{OV}=(v_x,v_y,v_z)\).
Si \((x_a,y_a,z_a)\) et \((x_b,y_b,z_b)\) sont respectivement les coordonnées des points \(A\) et \(B\), le vecteur \(\overrightarrow{AB}\) ou \(\vec{u}\) qu'ils définissent, a pour composantes \((u_x,u_y)=(x_b-x_a,y_b-y_a,z_b-z_a)\).
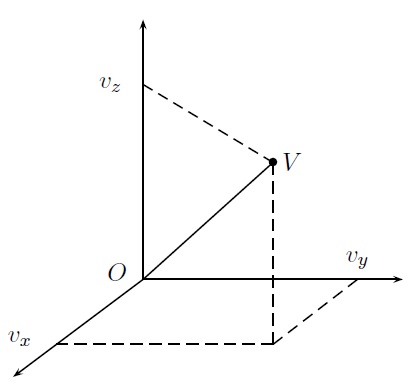
La définition de norme s'étend sans difficulté aux cas du vecteur dans l'espace.
\(\|\vec{v}\| =\sqrt{v_x^2+v_y^2+v_z^2}.\)
Si \(\vec{u}=\overrightarrow{AB}=(b_x-a_x,b_y-a_y,b_z-a_z)\) alors\(\|\vec{u}\| =\|\overrightarrow{AB}\| =\sqrt{(b_x-a_x)^2+(b_y-a_y)^2+(b_z-a_z)^2}.\)
Par exemple, considérons le vecteur \(\vec{u}=\overrightarrow{AB}\) où \(A=(3,1,-2)\) et \(B=(-2,7,-4)\).
Les composantes du vecteur \(\vec{u}\) se calculent par la différence entre les coordonnées du point \(B\) et celles du point \(A\) :
\(\vec{u}=(-2-3,7-1,-4+2)=(-5,6,-2).\)
La norme du vecteur \(\vec{u}\) se calcule par la formule
\(\|\vec{u}\|=\sqrt{(-5)^2+6^2+(-2)^2}=\sqrt{65}.\)
Opérations sur les vecteurs
Dans les applications, on distingue les grandeurs scalaires par opposition aux grandeurs vectorielles, c'est-à-dire aux vecteurs. Une grandeur scalaire est caractérisée par un seul nombre réel, alors qu'une grandeur vectorielle est caractérisée par deux ou trois nombres réels suivant que l'on se trouve dans le plan ou l'espace. Les opérations que l'on peut effectuer sur des grandeurs scalaires ne sont rien d'autre que celles que l'on peut effectuer sur les nombres réels. Par contre, on définit des opérations spécifiques aux vecteurs.
(a) L'addition vectorielle
On définit l'addition ou somme de deux vecteurs \(\vec{u}\) et \(\vec{v}\), comme le vecteur dont les composantes sont obtenues par addition des composantes correspondantes des deux vecteurs \(\vec{u}\) et \(\vec{v}\). On note \(\overrightarrow{u+v}\) le vecteur somme.
\(\vec{u}+\vec{v}=(u_x+v_x,u_y+v_y).\)
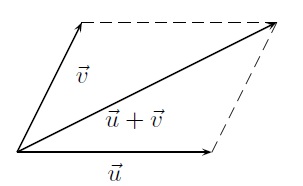
On peut donner une interprétation géométrique de cette opération. On considère le vecteur \(\vec{u}\) placé en n'importe quel point du plan. On place le vecteur \(\vec{v}\) à l'extrémité du vecteur \(\vec{u}\). Les deux vecteurs forment alors les côtés d'un parallélogramme dont la diagonale partant de l'origine de \(\vec{u}\) et arrivant à l'extrémité de \(\vec{v}\) est le vecteur somme \(\vec{u}+\vec{v}\).
\(\vec{u}+\vec{v}=(u_x+v_x,u_y+v_y,u_z+v_z).\)
Par exemple, la somme des deux vecteurs \(\vec{a}=(3,1,4)\) et \(\vec{b}=(1,-2,3)\) est le vecteur \(\vec{a}+\vec{b}=(3+1,1+(-2),4+3)=(4,-1,7)\).
Propriétés de l'addition vectorielle
- L'addition vectorielle est commutative : \(\vec{u} + \vec{v} = \vec{v} + \vec{u}\).
On constate que le vecteur \(\vec{v}+\vec{u}\) que l'on forme en additionnant \(\vec{v}\) et \(\vec{u}\) coïncide avec le vecteur \(\vec{u}+\vec{v}\).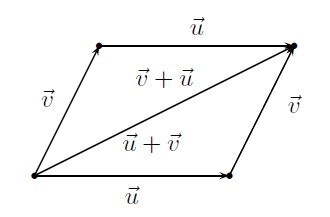
- L'addition vectorielle est associative : \(\vec{u}+(\vec{v}+\vec{w})=(\vec{u} + \vec{v}) + \vec{w}\). On constate que si l'on additionne \(\overrightarrow{OB}=\vec{u}+\vec{v}\) à \(\vec{w}\) on obtient le vecteur \(\overrightarrow{OC}=(\vec{u}+\vec{v})+\vec{w}\). On obtient ce même vecteur en additionnant au vecteur \(\vec{u}\), le vecteur \(\overrightarrow{AC}=\vec{v}+\vec{w}\). D'où \(\vec{u}+(\vec{v} + \vec{w})=(\vec{u} + \vec{v}) + \vec{w}\).
On remarquera que pour additionner \(n\) vecteurs, il suffit en partant d'une position arbitraire du premier vecteur, de placer successivement l'origine de chaque vecteur à l'extrémité du précédent.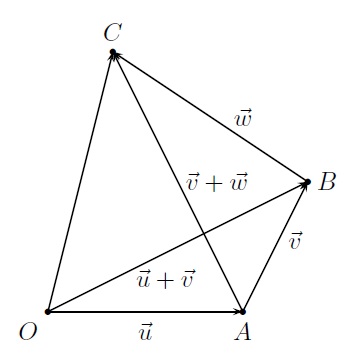
Le vecteur somme des \(n\)vecteurs est alors le vecteur dont l'origine est celle du premier et l'extrémité, celle du dernier. Dans cette opération, l'ordre des vecteurs dans la somme n'a pas d'importance. Cette opération peut se faire aussi bien dans l'espace que dans le plan.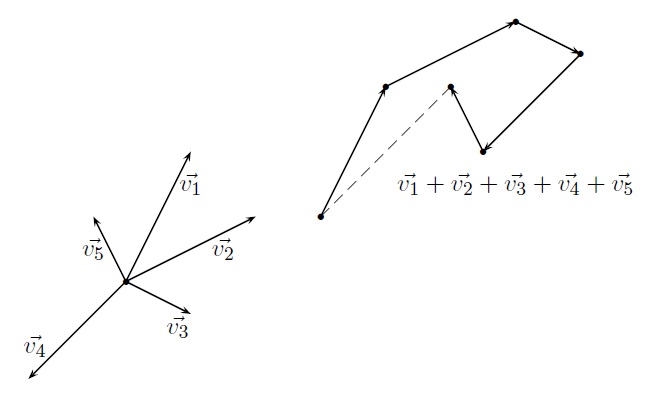
- L'addition vectorielle admet un élément neutre : \(\vec{v} + \vec{o} = \vec{v}\).
L'élément neutre est le vecteur nul ou zéro, noté \(\vec{o}\) et défini comme le vecteur dont toutes les composantes sont égales à zéro. Dans le plan, on a \(\vec{o}=(0,0)\) et dans l'espace \(\vec{o}=(0,0,0)\). Ces vecteurs ont une longueur nulle et par convention leur direction n'est pas définie. - L'addition vectorielle admet un opposé : \(\vec{v} + (-\vec{v})=\vec{o}\).
Le vecteur noté \(-\vec{v}\) et appelé vecteur opposé de \(\vec{v}\), dont les composantes sont les composantes du vecteur \(\vec{v}\), changées de signe. Dans le plan, si \(\vec{v}=(v_x,v_y)\) alors \(-\vec{v}=(-v_x,-v_y)\) et dans l'espace, si \(\vec{v}=(v_x,v_y,v_z)\) alors \(-\vec{v}=(-v_x,-v_y,-v_z)\). Le vecteur \(-\vec{v}\) a la même longueur que \(\vec{v}\), la même direction, mais est de sens opposé.
(b) La soustraction vectorielle
La soustraction vectorielle revient à une addition vectorielle : lorsqu'on veut soustraire le vecteur \(\vec{v}\) du vecteur \(\vec{u}\), on ajoute à \(\vec{u}\) l'opposé de \(\vec{v}\), c'est-à-dire
\(\vec{u}-\vec{v} = \vec{u} + (-\vec{v}).\)
\(\vec{u}-\vec{v}=(u_x-v_x,u_y-v_y).\)
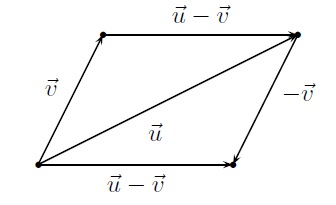
On constate que pour soustraire \(\vec{v}\) de \(\vec{u}\), il suffit de placer sur le même point les origines des deux vecteurs et de prendre comme origine et extrémité du vecteur \(\vec{u}-\vec{v}\) respectivement l'extrémité de \(\vec{v}\) et l'extrémité de \(\vec{u}\).
\(\vec{u}-\vec{v}=(u_x-v_x,u_y-v_y,u_z-v_z).\)
Par exemple, la différence des deux vecteurs \(\vec{a}=(3,1,4)\) et \(\vec{b}=(1,-2,3)\) est le vecteur \(\vec{a}-\vec{b}=(3-1,1-(-2),4-3)=(2,3,1)\).
(c) Multiplication d'un vecteur par un scalaire
La multiplication d'un vecteur \(\vec{v}\) par un scalaire \(\alpha\), notée \(\alpha\vec{v}\), est le vecteur dont les composantes sont celles de \(\vec{v}\) multipliées par \(\alpha\).
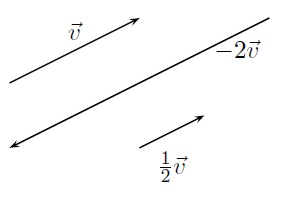
Géométriquement, cette opération revient à effectuer une contraction ou une dilatation du vecteur \(\vec{v}\), avec éventuellement un renversement de sens si le scalaire \(\alpha\) est négatif.
Par exemple, si \(\vec{v}=(1,2,3)\) et \(\alpha =4\) alors \(\alpha\vec{v}=(4,8,12)\).
Propriétés de la multiplication d'un vecteur par un scalaire
- Distributivité par rapport à l'addition dans \(\mathbb{R}\) : \((\alpha + \beta) \vec{v} = \alpha \vec{v} + \beta \vec{v}\).
- Distributivité par rapport à l'addition vectorielle : \(\alpha (\vec{u}+\vec{v}) = \alpha \vec{u} + \alpha \vec{v}\).
- Associativité mixte : \(\alpha (\beta \vec{v}) = (\alpha \beta) \vec{v}\).
- Elément neutre : \(1\cdot \vec{v} = \vec{v}$\).
On dira que deux vecteurs \(\vec{u}\) et \(\vec{v}\) du plan ou de l'espace :
- ont la même direction et sont de même sens si \(vec{u}=\alpha\vec{v}\), pour un certain \(\alpha>0\),
- ont la même direction et sont de sens contraire si \(\vec{u}=\alpha\vec{v}\), pour un certain \(\alpha<0\).
Par exemple, les vecteurs \(\vec{u}=(4,8,12)\) et \(\vec{v}=(1,2,3)\) sont parallèles car \(\vec{u}=4\, \vec{v}\).
(d) Le produit scalaire de deux vecteurs
Il s'agit d'une opération de multiplication entre deux vecteurs donnant comme résultat un scalaire, c'est-à-dire un nombre. Il est noté en général avec un point \(\vec{u}\cdot\vec{v}\). Pour le distinguer de la multiplication usuelle, nous le noterons \(\vec{u}\odot\vec{v}\). Dans un repère orthonormé, le produit scalaire de deux vecteurs est égal à la somme des produits de leurs composantes correspondantes.
\(\vec{u}\odot\vec{v}=u_x v_x + u_y v_y.\)
Dans l'espace, si \(\vec{u}=(u_x,u_y,u_z)\) et \(\vec{v}=(v_x,v_y,v_z)\) alors\(\vec{u}\odot\vec{v}=u_x v_x + u_y v_y + u_z v_z.\)
On appelle ce produit "scalaire" parce que son résultat est un nombre.
Par exemple, le produit scalaire des vecteurs \(\vec{u}=(2,3,4)\) et \(\vec{v}=(1,-2,2)\) est le nombre réel
\(\vec{u}\odot\vec{v}=2\cdot1 +3\cdot(-2)+4\cdot2=4.\)
Propriétés du produit scalaire
- Le produit scalaire d'un vecteur avec lui-même est égal au carré de sa longueur ou norme : \(\vec{v}\odot\vec{v}=\|\vec{v}\|^2.\)
- Le produit scalaire de deux vecteurs est commutatif : \(\vec{u}\odot\vec{v}=\vec{v}\odot\vec{u}.\)
- Il y a distributivité du produit scalaire par rapport à l'addition des vecteurs :
\(\vec{u}\odot(\vec{v}+\vec{w})=\vec{u}\odot\vec{v}+\vec{u}\odot\vec{w}.\) - Il y a associativité mixte : \((\alpha\vec{u})\odot\vec{v}=\alpha(\vec{u}\odot\vec{v})=\vec{u}\odot(\alpha\vec{v}).\)
- Le vecteur nul est absorbant pour le produit scalaire : \(\vec{o}\odot\vec{u}=0.\)
On peut définir le produit scalaire d'un point de vue géométrique.
\(\vec{u}\odot\vec{v}=\|\vec{u}\|\|\vec{v}\|\cos\theta.\)
En d'autres termes, le produit scalaire de deux vecteurs est égal au produit des normes des vecteurs par le cosinus de l'angle entre ceux-ci.
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
De la proposition, on peut déduire la formule suivante pour le cosinus de l'angle \(\theta\) que forment deux vecteurs \(\vec{u}\) et \(\vec{v}\).
Par exemple, l'angle entre les vecteurs \(\vec{a}=(4,-3)\) et \(\vec{b}=(1,2)\) est donné par
\(\cos\theta = \dfrac{\vec{a}\odot\vec{b}}{\|\vec{a}\|\|\vec{b}\|}= \dfrac{-2}{5\sqrt{5}},\)
et donc
\(\theta=\arccos\frac{-2}{5\sqrt{5}}\approx 100,3^\circ.\)
Dans ce cas, le cosinus de l'angle vaut \(0\) et on déduit de la proposition que le produit scalaire est nul.
Par exemple, les vecteurs \(\vec{a}=(\frac{1}{2},-3)\) et \(\vec{b}=(-2,12)\) sont parallèles. En effet, on a
\(\cos\theta = \dfrac{\vec{a}\odot\vec{b}}{\|\vec{a}\|\|\vec{b}\|}= \dfrac{-37}{37}=-1,\)
et donc
\(\theta=\arccos (-1)= \pi.\)
L'angle entre les deux vecteurs étant \(\pi\), ces deux vecteurs sont parallèles. De plus, on remarque que \(\vec{b}= -4 \vec{a}\).
Par contre, les vecteurs \(\vec{a}=(2,3)\) et \(\vec{b}=(6,-4)\) sont orthogonaux car \(\vec{a}\odot\vec{b}=2.6+ 3.(-4)=0\).
On peut démontrer les deux résultats suivants, relatifs à la longueur des vecteurs :
\((1)\) Inégalité de Cauchy-Schwartz : \(|\vec{u}\odot\vec{v}|\le \|\vec{u}\|\|\vec{v}\|\).
\((2)\) Inégalité triangulaire : \(\|\vec{u}+\vec{v}\|\le\|\vec{u}\|+\|\vec{v}\|\).
Cette inégalité spécifie que dans un triangle, la longueur d'un côté ne peut dépasser la somme des longueurs des deux autres côtés.
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
(e) Le produit vectoriel de deux vecteurs
A la différence du produit scalaire, qui est un nombre réel, le produit vectoriel de deux vecteurs est un vecteur, noté \(\vec{u}\times\vec{v}\) (ou encore \(\vec{u}\wedge\vec{v}\)). Pour le définir, on a besoin de la notion d'orientation d'un repère.
- \(\vec{u}\times\vec{v}\) est perpendiculaire à \(\vec{u}\) et à \(\vec{v}\);
- \(\|\vec{u}\times\vec{v}\|=\|\vec{u}\|\|\vec{v}\|\, |\sin{\theta}| \)
- les vecteurs \(\vec{u}\), \(\vec{v}\) et \(\vec{u}\times\vec{v}\)pris dans cet ordre forment un repère d'orientation directe.
Remarque : La longueur \(\|\vec{u}\times\vec{v}\|\) est l'aire du parallélogramme construit sur les vecteurs \(\vec{u}\) et \(\vec{v}\).
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
Propriétés du produit vectoriel
- Le produit vectoriel de deux vecteurs est anti-commutatif : \(\vec{u}\times\vec{v}=-(\vec{v}\times\vec{u}).\)
- Le produit vectoriel est linéaire à gauche : \(\vec{u}\times(\alpha\vec{v}+\beta\vec{w})=\alpha(\vec{u}\times\vec{v})+\beta(\vec{u}\times\vec{w}).\)
- Le produit vectoriel est linéaire à droite : \((\alpha\vec{u}+\beta\vec{v})\times\vec{w}=\alpha(\vec{u}\times\vec{w})+\beta(\vec{v}\times\vec{w}).\)
\(\vec{u}\times\vec{v}=(u_yv_z-u_zv_y,u_zv_x-u_xv_z, u_xv_y-u_yv_x).\)
Par exemple, si \(\vec{a}=(1,2,3)\) et \(\vec{b}=(6,5,4)\) alors le vecteur \(\vec{v}=\vec{a}\times \vec{b}=(2\cdot 4-3\cdot 5,3\cdot 6-1\cdot 4, 1\cdot 5-2\cdot 6)=(-7,14,-7)\) est perpendiculaire aux vecteurs \(\vec{a}\) et \(\vec{b}\). L'aire du parallélogramme construit sur \(\vec{a}\) et \(\vec{b}\). est
\(\|\vec{a}\times \vec{b}\|=\|\vec{v}\|=\sqrt{49+196+49}=\sqrt{294}=7\sqrt{6}.\)
Dans le cas où les deux vecteurs sont parallèles, le sinus de l'angle vaut \(0\) et on en déduit que le produit vectoriel est nul.
Par exemple, les vecteurs \(\vec{u}=(1,-2,3)\) et \(\vec{v}=(-2,4,-6)\)sont parallèles car
\(\vec{u}\times\vec{v}=(-2\cdot (-6)-3\cdot 4,3\cdot (-2)-(-6)\cdot 1, 1\cdot 4-(-2)\cdot (-2))=(0,0,0)=\vec{o}.\)
On a \(\vec{v}=-2\vec{u}\).
(f) Produit mixte
Si on dispose de 3 vecteurs donnés \(\vec u, \vec v \) et \(\vec w \), on peut considérer l'expression
\((\vec u \times \vec v) \odot \vec w \)
qui désigne un nombre réel, appelé produit mixte des 3 vecteurs .
Dans un repère cartésien orthonormé, on peut donner une signification géométrique intéressante à \(| (\vec u \times \vec v) \odot \vec w |\). En effet, ce nombre revient à \(\| \vec u \times \vec v \| \| \vec w \| | \cos (\vec u \times \vec v, \vec w ) | \). Si nous regardons le parallélipipède construit sur les 3 vecteurs, nous observons que \(\| \vec u \times \vec v \|\) donne l'aire de la base (construite sur \(\vec u\) et \(\vec v\)) et que \(\| \vec w \| |\cos (\vec u \times \vec v, \vec w)|\) donne la longueur de la projection orthogonale de \(\vec w \) sur la droite qui porte \(\vec u \times \vec v\), c'est-à-dire la hauteur du parallélipipède. Donc \(|(\vec u \times \vec v) \odot \vec w|\) donne le volume du parallélipipède.
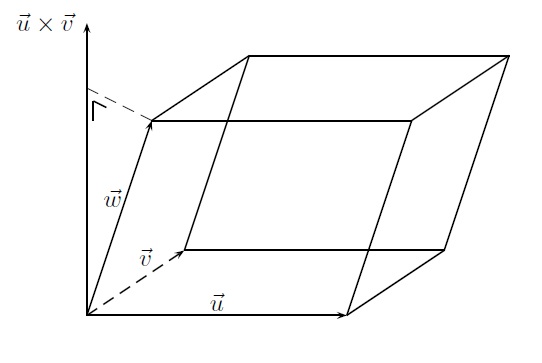
Vecteurs et points particuliers
(a) Vecteur normé
Etant donné un vecteur \(\vec{v}\), on est parfois amené à considérer un vecteur de longueur un, dans la même direction et dans le même sens que \(\vec{v}\). Notons \(\vec{1}_{v}\) ce vecteur. Pour l'obtenir, il suffit de diviser le vecteur \(\vec{v}\) par sa longueur. On dit d'un vecteur dont la norme est égale à un qu'il est normé.
Par exemple, le vecteur normé de même direction et de même sens que le vecteur \(\vec{v}=(-5,6,-2)\) est le vecteur
\(\vec{1}_{v}=\frac{\vec{v}}{\|\vec{v}\|}=\frac{(-5,6,-2)}{\sqrt{65}}= \left(-\frac{5}{\sqrt{65}},\frac{6}{\sqrt{65}}, -\frac{2}{\sqrt{65}}\right).\)
On a bien
\(\|\vec{1}_{v}\|=\left\|\left(-\frac{5}{\sqrt{65}},\frac{6}{\sqrt{65}}, -\frac{2}{\sqrt{65}}\right)\right\|=\sqrt{\frac{25}{65}+\frac{36}{65}+\frac{4}{65}}=1.\)
(b) Vecteurs colinéaires et orthogonaux
Rappelons que deux vecteurs \(\vec{u}\) et \(\vec{v}\) sont colinéaires s'ils ont même direction, et donc s'il existe \(\alpha\in \mathbb{R}\) tel que \(\vec{u}=\alpha\vec{v}\).
Deux vecteurs \(\vec{u}\) et \(\vec{v}\) sont orthogonaux s'ils forment un angle droit et donc si \(\vec{u}\odot\vec{v}=0\).
(c) Milieu d'un vecteur
Pour trouver le milieu d'un vecteur, on additionne les composantes de son origine et de son extrémité et on les divise par deux.
\((x_m,y_m) = \left(\frac{1}{2} (x_p + x_q),\frac{1}{2} (y_p+ y_q)\right).\)
Dans l'espace, si \(P = (x_p,y_p,z_p)\) et \(Q = (x_q,y_q,z_q)\) alors les coordonnées du point \(M\), milieu du vecteur \(\overrightarrow{PQ}\) sont données par\((x_m,y_m,z_m) =\left(\frac{1}{2} (x_p + x_q),\frac{1}{2} (y_p+ y_q),\frac{1}{2} (z_p+ z_q)\right).\)
(d) Vecteurs de base
Dans le cas du plan, les vecteurs \((1,0)\) et \((0,1)\) jouent un rôle particulier. Il s'agit des vecteurs unitaires parallèles aux axes. On peut exprimer tout vecteur \(\vec{v}\) de composantes \((v_x,v_y)\) comme combinaison linaire de ces deux vecteurs avec les composantes \((v_x,v_y)\) comme coefficients de la combinaison linéaire : \(\vec{v}=(v_x,v_y)=v_x(1,0)+v_y(0,1)\).
\(\vec{v}=(v_x,v_y)=v_x(1,0)+v_y(0,1).\)
Les vecteurs \((1,0)\) et \((0,1)\) sont appelés vecteurs de base. Le nombre \(v_x\) est appelé composante horizontale de \(\vec{v}\) et \(v_y\) est appelé composante verticale de \(\vec{v}\).Il en est de même des vecteurs \((1,0,0)\), \((0,1,0)\) et \((0,0,1)\) dans l'espace \(\mathbb{R}^3\).
\(\vec{v}=(v_x,v_y,v_z)=v_x(1,0,0)+v_y(0,1,0)+v_z(0,0,1).\)
Exemples détaillés
- Déterminer les coordonnées polaires du point \(P=(-\frac{\sqrt{2}}{4},\frac{\sqrt{2}}{4})\)
Solution détaillée : On a
\(r=\sqrt{\left(-\frac{\sqrt{2}}{4}\right)^2+\left(\frac{\sqrt{2}}{4}\right)^2}=\sqrt{\frac{2}{16}+\frac{2}{16}}=\sqrt{\frac{1}{4}}=\frac{1}{2} \)
et
\(\tan{\theta}=\frac{\frac{\sqrt{2}}{4}}{-\frac{\sqrt{2}}{4}}=-1\)
donc \(\theta=\frac{3\pi}{4}\) ou \(\theta=\frac{7\pi}{4}\). Les coordonnées cartésiennes indiquent que le point \(P\) se trouve dans le deuxième quadrant et donc \(\theta=\frac{3\pi}{4}\).
Le point \(P\) en coordonnées polaires s'écrit donc \(P=(\frac{1}{2}\cos{(\frac{3\pi}{4})},\frac{1}{2}\sin{(\frac{3\pi}{4})})\).
- Déterminer les coordonnées cartésiennes du point \(P\) si \(r=2\) et \(\theta=\frac{7\pi}{6}\).
Solution détaillée : On a
\(x=r\cos\theta=2\cos{\left(\frac{7\pi}{6}\right)}=2\cdot \left(-\frac{\sqrt{3}}{2}\right)=-\sqrt{3} \)
et
\(y=r\sin\theta=2\sin{\left(\frac{7\pi}{6}\right)}=2\cdot \left(-\frac{1}{2}\right)=-1.\)
Le point \(P\) a donc pour coordonnées cartésiennes \(P=(-\sqrt{3},-1)\).
- Déterminer la distance entre les points \((3,1)\) et \((2,4)\).
Solution détaillée : On calcule \(d=\sqrt{(2-3)^2+(4-1)^2}=\sqrt{1+9}=\sqrt{10}\).
- Donner l'équation du cercle de centre \((1,2)\) et passant par le point \((6,-1)\).
Solution détaillée : Le rayon de ce cercle est donné par la distance entre les points \((1,2)\) et \((6,-1)\). Ce rayon vaut donc \(r=\sqrt{(6-1)^2+(-1-2)^2}=\sqrt{25+9}=\sqrt{34}\).
Le cercle centré en \((1,2)\) et de rayon \(\sqrt{34}\) a pour équation
\((x-1)^2+(y-2)^2=34\)
ou encore
\(x^2-2x+y^2-4y=29.\)
- Déterminer le centre et le rayon de la sphère d'équation \(x^2+y^2+z^2-12x+14y-8z+1=0\).
Solution détaillée : On a successivement
\(\begin{array}{l} x^2-12x+y^2+14y+z^2-8z=-1\\ x^2-2\cdot 6\cdot x+36+y^2+2\cdot 7\cdot y+49+z^2-2\cdot 4\cdot z+16=-1+36+49+16\\ (x-6)^2+(y+7)^2+(z-4)^2=100 \end{array}\)
Il s'agit donc d'une sphère de centre \((6,-7,4)\) et de rayon \(10\).
- Déterminer \(\vec{a}+\vec{b}\), \(\vec{a}-\vec{b}\) et \((\vec{a}-4\vec{b})\) pour \(\vec{a}=(-2,6,1)\), \(\vec{b}=(3,-3,-1)\).
Solution détaillée : On a
\(\vec{a}+\vec{b}=(-2+3,6-3,1-1)=(1,3,0)\),
\(\vec{a}-\vec{b}=(-2-3,6-(-3),1-(-1))=(-5,9,2)\),
\((\vec{a}-4\vec{b})=(-2,6,1)-4(3,-3,-1)=(-2,6,1)-(12,-12,-4)=(-14,18,5)\).
- Etant donné \(\vec{a}=(-2,3,1)\), \(\vec{b}=(7,4,5)\) et \(\vec{c}=(1,-5,2)\), calculer les nombres \(\vec{a}\odot \vec{b}\), \(\vec{a}\odot(\vec{b}+\vec{c})\) et \(\vec{a}\odot\vec{b}+\vec{a}\odot\vec{c}\).
Solution détaillée : On a
\(\vec{a}\odot \vec{b}=-2\cdot 7+3\cdot 4+1\cdot 5=-14+12+5=3\),
\(\vec{a}\odot(\vec{b}+\vec{c})=(-2,3,1)\odot (8,-1,7)=-2\cdot 8+3\cdot (-1)+1\cdot 7=-12\),
\(\vec{a}\odot\vec{b}+\vec{a}\odot\vec{c}=-2\cdot 7+3\cdot 4+1\cdot 5+(-2)\cdot 1+3\cdot (-5)+1\cdot 2=-12\).
Remarquons que \(\vec{a}\odot(\vec{b}+\vec{c})=\vec{a}\odot\vec{b}+\vec{a}\odot\vec{c}\).
-
Etant donné \(\vec{a}=(1,0,2)\), \(\vec{b}=(-1,2,1)\) et \(\vec{c}=(0,1,-1)\), calculer les vecteurs \((\vec{a}\times\vec{b})\times\vec{c}\) et \(\vec{a}\times(\vec{b}\times\vec{c})\).
Solution détaillée : On a
\(\vec{a}\times\vec{b}=(0\cdot 1-2\cdot 2,2\cdot (-1)-1\cdot 1,1\cdot 2-0\cdot (-1))=(-4,-3,2)\),
\((\vec{a}\times\vec{b})\times\vec{c}=(-3\cdot (-1)-2\cdot 1,2\cdot 0-(-4)\cdot (-1),-4\cdot 1-(-3)\cdot 0)=(1,-4,-4)\).
D'autre part,
\(\vec{b}\times\vec{c}=(2\cdot (-1)-1\cdot 1,1\cdot 0-(-1)\cdot (-1),(-1)\cdot 1-0\cdot 2)=(-3,-1,-1)\),
\(\vec{a}\times(\vec{b}\times\vec{c})=(0\cdot (-1)-2\cdot (-1),2\cdot (-3)-1\cdot (-1),1\cdot (-1)-0\cdot (-3))=(2,-5,-1)\).
Remarquons que \((\vec{a}\times\vec{b})\times\vec{c}\neq\vec{a}\times(\vec{b}\times\vec{c})\).
-
Solution détaillée : On sait que \(\vec{a}\perp\vec{b}\Leftrightarrow \vec{a}\odot\vec{b}=0\).
On calcule \(\vec{a}\odot\vec{b}=4\cdot 2+(-1)\cdot (-2)+(-2)\cdot 5=0\), donc les vecteurs \(\vec{a}\) et \(\vec{b}\) sont orthogonaux.
-
Déterminer les valeurs de \(c\) pour que les vecteurs \(\vec{a}=(c,-2,3)\) et \(\vec{b}=(c,c,-5)\) soient orthogonaux.
Solution détaillée : On sait que \(\vec{a}\perp\vec{b}\Leftrightarrow \vec{a}\odot\vec{b}=0\).
Or \(\vec{a}\odot\vec{b}=c^2-2c-15\) et donc\(\begin{array}{rcl} \vec{a}\odot\vec{b}=0&\Leftrightarrow &c^2-2c-15=0, \\ &\Leftrightarrow &(c-5)(c+3)=0, \\ &\Leftrightarrow & c=5\mbox{ ou }c=-3. \end{array} \)
Pour plus de détails sur la factorisation, cliquez ici.
-
Soit \(P_1=(-1,2,3)\) et \(P_2=(2,-2,8)\). Donner les composantes du vecteur \(\overrightarrow{P_1P_2}\), sa longueur et les coordonnées du point M, milieu de \(\overrightarrow{P_1P_2}\). Déterminer aussi les coordonnées de \(P_3\) tel que \(\overrightarrow{P_1P_3}=3\, \overrightarrow{P_1P_2}\).
Solution détaillée : On a
\(\overrightarrow{P_1P_2}=(2-(-1),-2-2,8-3)=(3,-4,5\),
\(\|\overrightarrow{P_1P_2}\|=\sqrt{3^2+(-4)^2+5^2}=\sqrt{9+16+25}=\sqrt{50}=5\sqrt{2}\),
\(M=\frac{P_1+P_2}{2}=\frac{1}{2}(-1+2,2-2,3+8)=(\frac{1}{2},0,\frac{11}{2})\).
Soit \(P_3=(a,b,c)\). On a \(\overrightarrow{P_1P_3}=P_3-P_1=(a+1,b-2,c-3)\) et \(\overrightarrow{P_1P_2}=P_2-P_1=(2+1,-2-2,8-3)=(3,-4,5)\). Il faut donc que \(a+1=3\cdot 3=9\), \(b-2=3\cdot (-4)=-12\) et \(c-3=3\cdot 5=15\). Donc \(a=8\), \(b=-10\), \(c=18\) et \(P_3=(8,-10,18)\).
-
Le point \(P\) est soumis à deux forces \(\overrightarrow{PQ}\) et \(\overrightarrow{PR}\) d'intensités respectives de 5N et 8N (le Newton est l'unité de force). La direction de \(\overrightarrow{PQ}\) est N\(20^\circ\)E et la direction de \(\overrightarrow{PR}\) est N\(65^\circ\)O. Donner les composantes horizontales et verticales de \(\overrightarrow{PQ}\) et \(\overrightarrow{PR}\).
Solution détaillée : On peut repésenter la situation à l'aide du schéma suivant :

On a \(\|\overrightarrow{PQ} \|=5\) et \(\|\overrightarrow{PR} \|=8\). Soit \((a,b)\) les composantes de \(\overrightarrow{PQ}\) et \((c,d)\), les composantes de \(\overrightarrow{PR}\).
On calcule \(a=\|\overrightarrow{PQ} \|\, \cos{(90^{\circ}-20^{\circ})}=5\cos{70^{\circ}}\) et \(b=\|\overrightarrow{PQ} \|\, \sin{(90^{\circ}-20^{\circ})}=5\sin{70^{\circ}}\). La composante horizontale de \(\overrightarrow{PQ}\) est \(a=5\cos{70^{\circ}}\) et la composante verticale de \(\overrightarrow{PQ}\) est \(b=5\sin{70^{\circ}}\).
De même, \(c=-\|\overrightarrow{PR} \|\, \cos{(90^{\circ}-65^{\circ})}=-8\cos{25^{\circ}}\) et \(d=\|\overrightarrow{PR} \|\, \sin{(90^{\circ}-65^{\circ})}=8\sin{25^{\circ}}\). La composante horizontale de \(\overrightarrow{PR}\) est \(c=-8\cos{25^{\circ}}\) et la composante verticale de \(\overrightarrow{PR}\) est \(d=8\sin{25^{\circ}}\).
-
Deux forces \(\vec{F_1}\) et \(\vec{F_2}\) qui agissent simultanément sur un point matériel \(P\) ont une action équivalente à une force unique appelée résultante \(\vec{R}\). Cette résultante est obtenue en traçant la diagonale du parallélogramme construit sur les vecteurs \(\vec{F_1}\) et \(\vec{F_2}\).
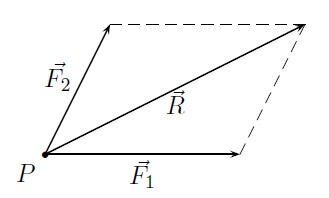
Dans la construction de la résultante, il suffit de tracer la moitié du parallélogramme où l'on place bout à bout les vecteurs \(\vec{F_1}\) et \(\vec{F_2}\). On a \(\vec{R}=\vec{F_1}+\vec{F_2}\).
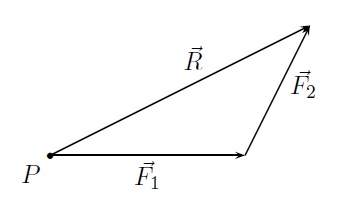
-
L'intensité et la direction d'une force constante sont données par \(\overrightarrow{a}= (2,5)\). Calculer le travail effectué si le point d'application de la force se déplace de l'origine au point \(P=(4,1)\).
Solution détaillée : Si \(\vec{F}\) est une force constante et \(\vec{d}\) représente le déplacement, on a \(W=\vec{F}\odot\vec{d}\). Ici, \(\vec{F}=\vec{a}=(2,5)\), \(\vec{d}=\overrightarrow{OP}= (4,1)\) et donc \(W=\vec{F}\odot\vec{d}=2\cdot 4+5\cdot 1=13\) Joules.
-
Sur un plan incliné dont la pente fait un angle de \(30^{\circ}\) avec l'horizontale, on pousse vers le haut un petit wagonnet pesant 500 N. Calculer le travail effectué pour compenser la force de gravitation si l'on pousse le wagonnet sur une distance de 24 m.
Solution détaillée : Représentons schématiquement le problème dans un système de coordonnées :
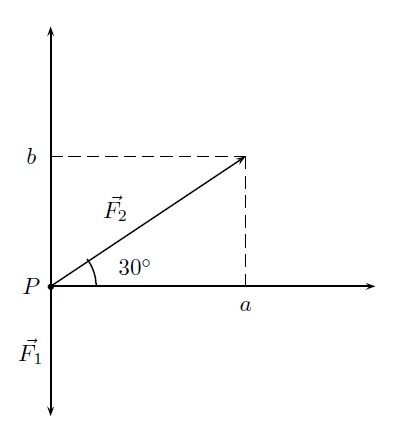
Le vecteur \(\vec{F_1}=(0,-500)\) représente la force de gravitation orientée vers le bas d'une intensité de 500 N. Le point d'application de cette force se déplace le long du vecteur \(\vec{F_2}\) de norme 24. Les composantes de ce vecteur sont \(a=\|\vec{F_2}\|\, \cos{30^{\circ}}= 24\cdot\frac{\sqrt{3}}{2}= 12\sqrt{3}\) et \(b=\|\vec{F_2}\|\, \sin{30^{\circ}}=24\cdot\frac{1}{2}= 12\). Donc \(\vec{F_2}=(12\sqrt{3},12)\) et \(W=\vec{F_1}\odot\vec{F_2}= (0,-500)\odot(12\sqrt{3}, 12) =-6000\). Le travail effectué pour compenser la force de gravitation est donc de 6000 Joules.
Preuves
Si \(\theta\) désigne l'angle entre les deux vecteurs non nuls \(\vec{u}\) et \(\vec{v}\), alors
\(\vec{u}\odot\vec{v}=\|\vec{u}\|\|\vec{v}\|\cos\theta.\)
Travaillons dans l'espace. Soit \(\vec{u}=(u_x,u_y,u_z)\) et \(\vec{v}=(v_x,v_y,v_z)\).
Cas 1 : Les vecteurs \(\vec{u}\) et \(\vec{v}\) ne sont pas colinéaires.
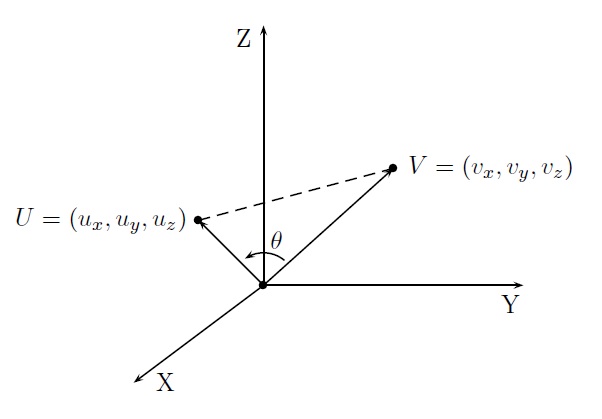
La Règle des cosinus permet d'écrire
\(\|\overrightarrow{UV}\|^2=\|\vec{u}\|^2+\|\vec{v}\|^2-2\|\vec{u}\|\|\vec{v}\|\cos\theta.\)
D'où
\((v_x-u_x)^2 + (v_y-u_y)^2 + (v_z-u_z)^2= (u_x^2+u_y^2+u_z^2)+(v_x^2+v_y^2+v_z^2)-2\|\vec{u}\|\|\vec{v}\|\cos\theta.\)
On peut simplifier cette dernière expression en
\(-2u_xv_x-2u_yv_y-2u_zv_z=-2\|\vec{u}\|\|\vec{v}\|\cos\theta,\)
ce qui par division des deux membres par \(-2\) donne le résultat recherché.
Cas 2 : Les vecteurs \(\vec{u}\) et \(\vec{v}\) sont colinéaires, c'est-à-dire il existe \(\alpha\in \mathbb{R}\) tel que \(\vec{v} = \alpha\vec{u}\). On a en vertu des propriétés du produit scalaire,
\(\vec{u}\odot\vec{v}=\vec{u}\odot(\alpha\vec{u})= \alpha(\vec{u}\odot\vec{u})=\alpha\|\vec{u}\|^2.\)
De même, on a
\(\|\vec{u}\|\|\vec{v}\|\cos\theta=\|\vec{u}\|\|\alpha\vec{u}\|\cos\theta =|\alpha|\|\vec{u}\|^2\cos\theta.\)
Si \(\alpha>0\), alors \(|\alpha|=\alpha\), \(\theta=0\) et \(|\alpha|\|\vec{u}\|^2\cos\theta=\alpha\|\vec{u}\|^2=\vec{u}\odot\vec{v}\).
Si \(\alpha<0\), alors \(|\alpha|=-\alpha\), \(\theta=\pi\) et \(|\alpha|\|\vec{u}\|^2\cos\theta=-\alpha\|\vec{u}\|^2\cdot(-1)=\alpha\|\vec{u}\|^2=\vec{u}\odot\vec{v}\).
Soit \(\vec{u}\) et \(\vec{v}\) deux vecteurs.
\((1)\) Inégalité de Cauchy-Schwartz : \(|\vec{u}\odot\vec{v}|\le \|\vec{u}\|\|\vec{v}\|\).
\((2)\) Inégalité triangulaire : \(\|\vec{u}+\vec{v}\|\le\|\vec{u}\|+\|\vec{v}\|\)
Cette inégalité spécifie que dans un triangle, la longueur d'un côté ne peut dépasser la somme des longueurs des deux autres côtés.
\((1)\) En utilisant la Proposition, on obtient
\(\begin{array}{rcl} |\vec{u}\odot \vec{v}|&=&|\, \|\vec{u}\|\|\vec{v}\|\cos{\theta}|\\ &=&\|\vec{u}\|\|\vec{v}\||\cos{\theta}|\\ &\leq&\|\vec{u}\|\|\vec{v}\|. \end{array}\)
\((2)\) En utilisant l'inégalité ci-dessus et les propriétés du produit scalaire, on obtient
\(\begin{array}{rcl} \|\vec{u}+\vec{v}\|^2&=&(\vec{u}+\vec{v})\odot (\vec{u}+\vec{v})\\ &=&\vec{u}\odot \vec{u}+\vec{u}\odot \vec{v}+\vec{v}\odot \vec{u}+\vec{v}\odot \vec{v}\\ &=&\|\vec{u}\|^2+2\, \vec{u}\odot \vec{v}+\|\vec{v}\|^2\\ &\leq&\|\vec{u}\|^2+2\, \|\vec{u}\|\, \|\vec{v}\|+\|\vec{v}\|^2\\ &=&(\|\vec{u}\|+\|\vec{v}\|)^2. \end{array}\)
En prenant la racine carrée des deux membres (qui sont positifs), on trouve
\(\|\vec{u}+\vec{v}\|\le\|\vec{u}\|+\|\vec{v}\|. \)
Construisons la figure suivante :
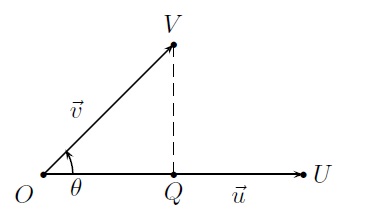
Soit \(Q\) la projection orthogonale de \(V\) sur \(\vec{u}\).
La longueur \(\|\overrightarrow{QV}\|\) représente la hauteur du parallélogramme construit sur \(\vec{u}\) et \(\vec{v}\). L'aire de ce parallélogramme est donc donnée par \(\|\vec{u}\|\cdot\|\overrightarrow{QV}\|\) et comme
\(|\sin{\theta}|=\frac{\|\overrightarrow{QV}\|}{\|\overrightarrow{OV}\|}=\frac{\|\overrightarrow{QV}\|}{\|\vec{v}\|},\)
on obtient
\(\mbox{Aire}=\|\vec{u}\|\, \|\vec{v}\|\, |\sin{\theta}|=\|\vec{u}\times\vec{v}\|.\)
Dans \(\mathbb{R}^3\), la distance entre deux points \(P=(x_p,y_p,z_p)\) et \(Q=(x_q,y_q,z_q)\) est donnée par la formule
\(d(P,Q)= \sqrt{(x_q -x_p)^2 + (y_q-y_p)^2+(z_q-z_p)^2}.\)
Construisons la figure suivante :
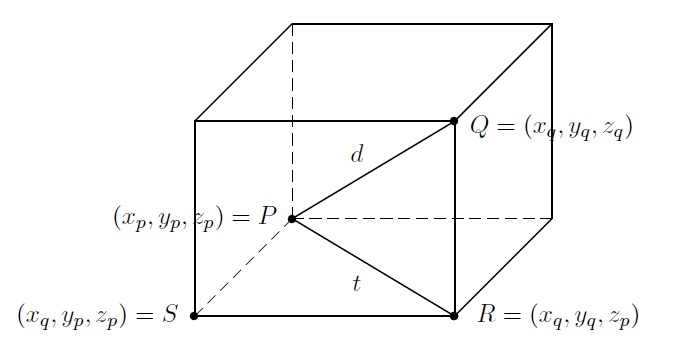
Si \(P=(x_p,y_p,z_p)\) et \(Q=(x_q,y_q,z_q)\) alors on a \(R=(x_q,y_q,z_p)\) et \(S=(x_q,y_p,z_p)\).
Dans le plan \(PSR\), le triangle \(PSR\) est rectangle en \(S\) et par le Théorème de Pythagore, on obtient
\(t^2=(x_q-x_p)^2+(y_q-y_p)^2.\)
Dans le plan \(PQR\), le triangle \(PQR\) est rectangle en \(R\) et par le Théorème de Pythagore, on obtient
\(d^2=t^2+(z_q-z_p)^2.\)
Finalement, on a
\(d^2=(x_q-x_p)^2+(y_q-y_p)^2+(z_q-z_p)^2.\)
