Théorie du module : Statistiques descriptives
Table des matières
- Définitions et exemples
- Préparation des données -- observations et modalités
- Distribution des données -- fréquences et effectifs
- Représentations graphiques
- Indicateurs numériques
- Exemples détaillés
Indicateurs numériques
L'ultime étape de toute description d'un jeu de données consiste en le calcul d'indicateurs numériques de "tendance"; ces indicateurs sont appelés statistiques.
(a) Indicateurs de position - moyenne, médiane et mode
Ces paramètres permettent de caractériser l'ordre de grandeur des observations. Ils servent comme indication de premier ordre sur la "tendance générale" du phénomène auquel on s'intéresse.
Définition - Soit un échantillon de \(n\) valeurs observées \(x_1, x_2, \ldots, x_n\) d'une variable quantitative \(X \). La moyenne arithmétique de la population est
\(\bar{x} = \dfrac{1}{n}\displaystyle \sum_{i=1}^n x_i. \)
Si la variable a \(M\) modalités \(y_1, y_2, \ldots, y_M\) d'effectifs respectifs \(n_{1}, n_2, \ldots, n_M\) et de fréquences respectives \(f_1, f_2, \ldots, f_M\) alors on obtient les formules équivalentes
\(\bar{x} =\displaystyle \sum_{i=1}^M y_i \frac{n_i}{n} = \sum_{i=1}^My_i f_i.\)
Par exemple, les données de la Table 10 représentent les résultats obtenus par 617 étudiants ayant passé un examen de BA1 dans une université belge en 2012.

Table 10 : Résultats obtenus par 617 étudiants à un examen; données brutes.
Ces données sont présentées après rangement dans la Table 11; la distribution (diagramme en bâtons) est représentée à la Figure 4.
\( \begin{array}{|c|c|c|c|c|} \hline \mbox{Cote } y_i & n_i & n_icc & f_i & f_icc \\ \hline 0 & 88& 88& 14,3\%& 14,3\%\\ 1& 13& 101& 2,1\%& 16,4\%\\ 2& 55& 156& 8,9\%& 25,3\%\\ 3& 71& 227& 11,5\%& 36,8\%\\ 4& 72& 299& 11,7\%& 48,5\%\\ 5& 56& 355& 9,1\%& 57,5\%\\ 6& 44& 399& 7,1\%& 64,7\%\\ 7& 41& 440& 6,6\%& 71,3\%\\ 8& 34& 474& 5,5\%& 76,8\%\\ 9& 26& 500& 4,2\%& 81,0\%\\ 10& 43& 543& 7,0\%& 88,0\%\\ 11& 14& 557& 2,3\%& 90,3\%\\ 12& 18& 575& 2,9\%& 93,2\%\\ 13& 15& 590& 2,4\%& 95,6\%\\ 14& 5& 595& 0,8\%& 96,4\%\\ 15& 5& 600& 0,8\%& 97,2\%\\ 16& 7& 607& 1,1\%& 98,4\%\\ 17& 2& 609& 0,3\%& 98,7\%\\ 18& 4& 613& 0,6\%& 99,4\%\\ 19& 4& 617& 0,6\%& 100,0\%\\ 20& 0& 617& 0,0\%& 100,0\%\\ \hline \end{array}\)
Table 11 : Résultats (entre 0/20 et 20/20) en BA1 à un examen, avec effectifs, fréquences, effectifs cumulés et fréquences cumulées.
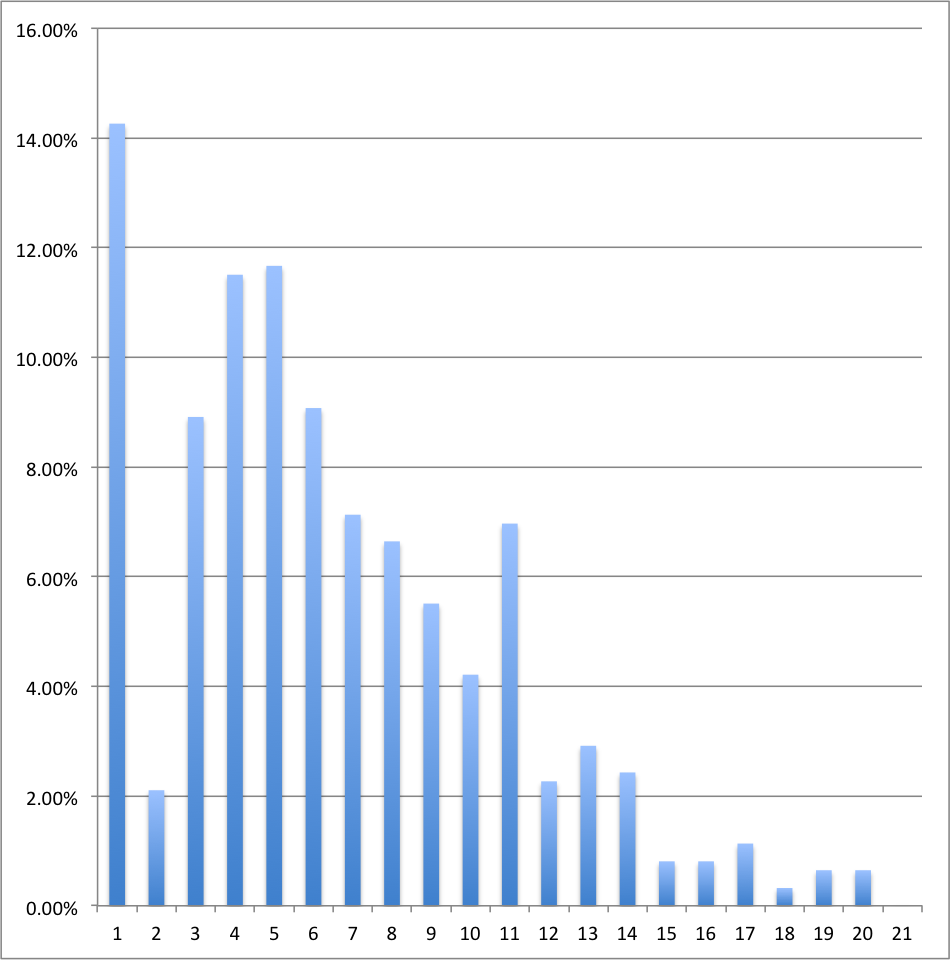
Figure 4 : Diagramme en bâtons des données de la Table 11.
On calcule la cote moyenne
\(\begin{array}{rcl} \bar{x} & =& \dfrac{1}{617} \left( 5+1+9+\ldots + 5+4+2 \right)\\ & =& \dfrac{1}{617} \left( 88\times0 + 13 \times 1 + \ldots + 4 \times 19 + 0 \times 20 \right) \\ & =& \displaystyle\sum_{i=1}^{20}y_if_i \\ & =& 5,5. \end{array}\)
Considérons les données de la Table 1. On calcule le prix moyen de location
\(\bar{x} = \dfrac{1}{200} \left( 350+370+375 + \ldots + 635+630\right) = 518,48\$ .\)
Si l'on ne dispose pas des données brutes mais seulement des données groupées en classe de la Table 4 alors on calcule la moyenne en utilisant les centres de classe
\(\bar{x} = \dfrac{1}{200}\left( 365\times 3 + \ldots + 635 \times 12\right) = 523,25\$.\)
La différence entre les deux valeurs est due à la perte d'informations entre le passage de la Table 1 à la Table 4.
La médiane est donc le "centre" de la population classée par ordre croissant.
Par exemple, considérons l'échantillon classé \(\left\{ 1, 3, 5, 7, 9\right\} \). La médiane est la valeur centrale, soit \(x_{med} = 5 \).
Il n'y a parfois pas de valeur pour laquelle les fréquences cumulées atteignent exactement \(50\%\). Dans ce cas on a deux possibilités pour calculer la médiane.
- Lorsqu'on dispose du jeu de \(n\) données brutes, on les range par ordre croissant \( x_1 \le x_2 \le \ldots \le x_n\) et
- si \(n\) est impair alors \(x_{med}=x_{(n-1)/2+1}\) est la médiane de la population;
- si \(n\) est pair alors \(x_{med} = \frac{x_{n/2}+x_{n/2+1}}{2}\) est une médiane de la population.
- Lorsque la distribution de l'échantillon est connue on appelle médiane la modalité (ou le centre de la classe) pour laquelle la fréquence cumulée dépasse \(50\%\) pour la première fois.
Par exemple, pour l'échantillon classé \(\left\{ 1, 3, 5, 7, 9, 20\right\} \), la médiane est la valeur centrale, soit \(x_{med} = (5+7)/2 = 6 \). Pour l'échantillon classé \(\left\{ 1, 3, 5, 7, 93, 1250\right\} \), la médiane est la valeur centrale, soit \(x_{med} = (5+7)/2 = 6 \).
Si on reprend les données de la Table 11, la cote médiane se situe entre 4/20 et 5/20.
Pour les données de la Table 8, le loyer médian se situe quelque part dans la classe \([500, 530[ \). En reprenant les données brutes de la Table 1 on obtient que le loyer médian est de \(520\$\).
Par exemple, dans l'échantillon classé \(\left\{ 1, 3, 5, 7, 9, 20\right\}\) toutes les données apparaissant le même nombre de fois (une seule), elles sont toutes des modes.
Dans l'échantillon classé \(\left\{ 1, 1, 3, 5,5, 5, 7, 9, 20, 20\right\}\) la valeur \(5\) apparait trois fois et est donc la plus fréquente. Le mode de cet échantillon est donc \(x_{mod} = 5 \).
Dans l'échantillon classé \(\left\{ 1, 1,1, 3, 5,5, 5, 7, 9, 20, 20\right\}\) les valeurs \(1\) et \(5\) apparaissent trois fois toutes les deux. Elles sont toutes deux des modes pour cet échantillon : \(x_{mod} = \left\{ 1, 5 \right\} \).
Si on reprend les données de la Table 11, la cote la plus fréquente est 0/20. Le mode est donc \(x_{mod} = 0 \).
(b) Indicateurs de dispersion -- amplitude, variance et écart-type
Les indicateurs de position ne sont qu'une première approximation et ne résument (bien entendu) pas le jeu de données.
Considérons un étudiant qui a une cote moyenne, sur 5 examens, de 8/20. Il pourrait avoir obtenu par exemple les résultats 0, 20, 12, 8, 0 ou bien les résultats 8, 8, 8, 8, 8. Bien que possédant la même moyenne et la même médiane, les deux séries de cotes s'interprètent de façon totalement différente !
Une façon de capter (et par suite d'interpréter) le type de différence illustré à l'exemple ci-dessus consiste à étudier la dispersion de la population observée.
Définition - L'amplitude d'un jeu de données \(x_1, x_2, \ldots, x_n\) est donné par
\(\mbox{Amplitude} = x_{\mathrm{max}}- x_{\mathrm{min}}\)
où \(x_{\mathrm{max}} \) est la valeur la plus grande prise par la variable et \(x_{\mathrm{min}}\) est la valeur minimale prise par la variable.
Définition - Soit une population de \(n\) valeurs observées \(x_1, x_2, \ldots, x_n\) d'un caractère quantitatif \(X\) et soit \(\bar{x}\) sa moyenne arithmétique observée. On définit la variance observée \(s^2\) comme la moyenne arithmétique des carrés des écarts à la moyenne
\(s^2 = \dfrac{1}{n}\displaystyle \sum_{i=1}^n \left( x_i-\bar{x} \right)^2.\)
Si la variable a \(M\) modalités \(y_1, y_2, \ldots, y_M\) d'effectifs respectifs \(n_1, n_2, \ldots, n_M\) et de fréquences respectives \(f_1, f_2, \ldots, f_M\) alors on a les formules équivalentes
\(s^2 = \displaystyle\sum_{i=1}^M (y_i-\bar{x})^2 \frac{n_i}{n} = \sum_{i=1}^M(y_i-\bar{x})^2 f_i.\)
Le théorème suivant permet de faciliter le calcul de la variance.
\(s^2 = \left( \dfrac{1}{n}\displaystyle \sum_{i=1}^n x_i^2 \right)- (\bar{x})^2.\)
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
La variance étant obtenue en prenant le carré des observations, elle ne s'exprime pas dans les mêmes unités que la population. Pour l'interprétation, on utilisera donc l'écart-type.
Par exemple, dans l'échantillon \(\left\{ 1, 1, 1, 1, 1\right\}\) toutes les données sont égales : il n'y a pas de variabilité et \(s^2 = s = 0 \).
Dans l'échantillon \(\left\{ 1, 3, 5, 7, 9, 20\right\} \), la moyenne est \(7,5\). La variance est donc
\(\begin{array}{rcl} s^2 &=& \dfrac{ (1-7,5)^2+ (3-7,5)^2+(5-7,5)^2+(7-7,5)^2+(9-7,5)^2+(20-7,5)^2 }{6}\\ & =& \dfrac{1^2+3^2+5^2+7^2+9^2+20^2}{6}-(7,5)^2\\ & = &37,91. \end{array}\)
Prenant la racine carrée de ce nombre on obtient l'écart-type \(s=6,15 \).
Reprenons le jeu de données de la Table 11. Rappelons-nous que la cote moyenne sur cet échantillon est de 5,5. Par facilité de calcul on rajoute dans la table une colonne contenant le carré des différences entre les modalités et la moyenne (cf. Table 12). Prenant la moyenne de cette dernière colonne, on obtient une variance de 17,75 et un écart-type de 4,21.
\(\begin{array}{|c|c|c|c|c|c|} \hline \mbox{Cote }y_i & n_i & n_icc & f_i & f_icc & (y_i-\bar{x})^2 \\ \hline 0 & 88& 88& 14,3\%& 14,3\% & 30,27\\ 1& 13& 101& 2,1\%& 16,4\% & 20,27 \\ 2& 55& 156& 8,9\%& 25,3\% & 12,26 \\ 3& 71& 227& 11,5\%& 36,8\% & 6,26 \\ 4& 72& 299& 11,7\%& 48,5\% & 2,25 \\ 5& 56& 355& 9,1\%& 57,5\% & 0,25\\ 6& 44& 399& 7,1\%& 64,7\% & 0,24\\ 7& 41& 440& 6,6\%& 71,3\% & 2,242\\ 8& 34& 474& 5,5\%& 76,8\% & 6,23\\ 9& 26& 500& 4,2\%& 81,0\% & 12,23\\ 10& 43& 543& 7,0\%& 88,0\% & 20,22\\ 11& 14& 557& 2,3\%& 90,3\% & 30,22\\ 12& 18& 575& 2,9\%& 93,2\% & 42,21\\ 13& 15& 590& 2,4\%& 95,6\% & 56,21\\ 14& 5& 595& 0,8\%& 96,4\% & 72,20\\ 15& 5& 600& 0,8\%& 97,2\% & 90,20\\ 16& 7& 607& 1,1\%& 98,4\% & 110,19\\ 17& 2& 609& 0,3\%& 98,7\% & 132,19\\ 18& 4& 613& 0,6\%& 99,4\% & 156,18\\ 19& 4& 617& 0,6\%& 100,0\% & 182,18\\ 20& 0& 617& 0,0\%& 100,0\% & 210,17\\ \hline \end{array}\)
Table 12 : Résultats (entre 0/20 et 20/20) en BA1 à un examen, avec effectifs, fréquences, effectifs cumulés et fréquences cumulées et une colonne contenant les carrés de différences entre valeurs et moyenne.
