Théorie du module : Géométrie et mesure
Table des matières
- Théorème de Thalès et proportions
- Cercles
- Polygones
- Triangles
- Quadrilatères
- Périmètre et aire de surfaces élémentaires
- Volume de solides élémentaires
- Mesures et grandeurs
- Exemples détaillés
Théorème de Thalès et proportions
(a) Rapports et proportions
Si \(a,\, b\in\mathbb{R}\) et \(b\neq 0\) alors le nombre réel \(\frac{a}{b}\) est appelé rapport des nombres \(a\) et \(b\). Une proportion est une égalité entre deux rapports non nuls. Si \(a\), \(b\), \(c\), \(d\in\mathbb{R}_0\) alors \(\frac{a}{b}=\frac{c}{d}\) est une proportion où \(a\) et \(d\) sont les extrèmes et \(b\) et \(c\) sont les moyens. On dit que les nombres \(a\) et \(b\) sont proportionnels aux nombres \(c\) et \(d\) si \(\frac{a}{b}=\frac{c}{d}\).
\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow ad=bc.\)
Dans une proportion on peut donc permuter les moyens et permuter les extrèmes.
(b) Théorème de Thalès
La propriété dite "petite propriété de Thalès" concerne un triangle coupé par une droite parallèle à l'un de ses côtés.
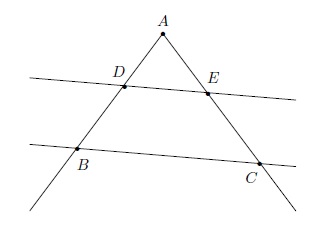
Cette propriété est généralisée avec deux triangles partageant un même sommet, ayant chacun deux côtés dans le prolongement l'un de l'autre et leur troisième côté parallèle.
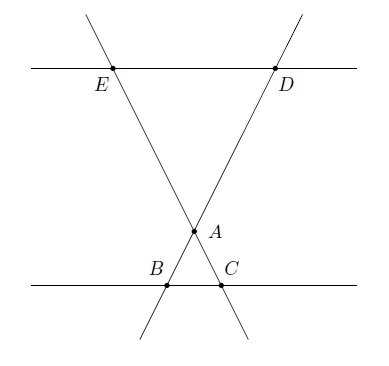
Pour résumer, lorsque nous sommes dans une situation telle que nous avons
- deux droites sécantes,
- deux points supplémentaires sur chacune des deux droites,
- deux droites parallèles passant par ces points,
nous pouvons appliquer le Théorème de Thalès qui énonce que le rapport de la plus petite mesure sur la plus grande pour chacun des deux segments des 2 droites sécantes et le rapport de la plus petite mesure sur la plus grande pour les segments qui représentent les droites parallèles sont égaux. Dans les deux cas ci-dessus, les droites DE et BC sont parallèles et nous avons les égalités
\(\dfrac{\vert AD\vert}{\vert AB\vert}=\dfrac{\vert AE\vert}{\vert AC\vert}=\dfrac{\vert DE\vert}{\vert BC\vert}.\)
En réalité, le Théorème de Thalès concerne une propriété plus générale.
\(\dfrac{\vert A'B'\vert}{\vert AB\vert}=\dfrac{\vert B'C'\vert}{\vert BC\vert}=\dfrac{\vert A'C'\vert}{\vert AC\vert}.\)
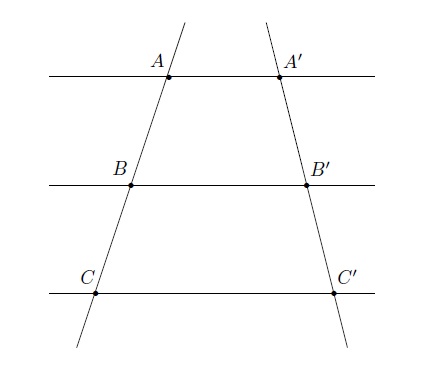
En permutant les termes moyens des fractions, on peut faire naître d'autres égalités de rapports :
\( \dfrac{\vert A'B'\vert}{\vert B'C'\vert}=\dfrac{\vert AB\vert}{\vert BC\vert},\qquad \dfrac{\vert B'C'\vert}{\vert A'C'\vert}=\dfrac{\vert BC\vert}{\vert AC\vert}, \qquad \dfrac{\vert A'B'\vert}{\vert A'C'\vert}=\dfrac{\vert AB\vert}{\vert AC\vert}.\)
Ces rapports traduisent la propriété suivante : la projection d'une droite sur une autre, suivant une direction donnée, conserve les proportions.
