Théorie du module : Géométrie et mesure
Table des matières
- Théorème de Thalès et proportions
- Cercles
- Polygones
- Triangles
- Quadrilatères
- Périmètre et aire de surfaces élémentaires
- Volume de solides élémentaires
- Mesures et grandeurs
- Exemples détaillés
Exemples détaillés
- Combien font 25 dam en km ?
Solution détaillée : On construit le tableau suivant :
| km | hm | dam | m | dm | cm | mm |
| 2 | 5 | |||||
| 0, | 2 | 5 |
On en conclut que 25 dam=0,25 km.
- Combien font 250 cm\(^2\) en m\(^2\) ?
Solution détaillée : On construit le tableau suivant :
| km\(^2\) | hm\(^2\) | dam\(^2\) | m\(^2\) | dm\(^2\) | cm\(^2\) | mm\(^2\) | |||||||
| 2 | 5 | 0 | |||||||||||
| 0, | 0 | 2 | 5 | ||||||||||
On en conclut que 250 cm\(^2\)=0,025 m\(^2\).
- Combien font 0,5 m\(^3\) en cm\(^3\) ?
Solution détaillée : On construit le tableau suivant :
| km\(^3\) | hm\(^3\) | dam\(^3\) | m\(^3\) | dm\(^3\) | cm\(^3\) | mm\(^3\) | ||||||||||||||
| 0, | 5 | |||||||||||||||||||
| 5 | 0 | 0 | 0 | 0 | 0 | |||||||||||||||
On en conclut que 0,5 m\(^3\)=500000 cm\(^3\).
- Combien d'eau font 3 l en cm\(^3\) ?
Solution détaillée : On construit le tableau suivant :
| kl | hl | dal | l | dl | cl | ml | ||||||||||||||
| km\(^3\) | hm\(^3\) | dam\(^3\) | m\(^3\) | dm\(^3\) | cm\(^3\) | mm\(^3\) | ||||||||||||||
| 3 | ||||||||||||||||||||
| 3 | 0 | 0 | 0 | |||||||||||||||||
On en conclut que 3 l=3 dm\(^3\)=3000 cm\(^3\).
- Combien font 100 km/h en m/s ?
Solution détaillée : On a
\(\begin{array}{ccc} 100\mbox{ km} & \longrightarrow & 1\mbox{ h} \\ 100000\mbox{ m} & \longrightarrow & 3600\mbox{ s} \\ \dfrac{100000}{3600}\mbox{ m} & \longrightarrow & 1\mbox{ s} \end{array} \)
La vitesse est donc \(\dfrac{100000}{3600}=\dfrac{250}{9}\) mètres par seconde.
- Combien font 2 m/s en km/h ?
Solution détaillée :
\(\begin{array}{ccc} 2\mbox{ m} & \longrightarrow & 1\mbox{ s} \\ 2\cdot 3600\mbox{ m} & \longrightarrow & 3600\mbox{ s} \\ 7200\mbox{ m} & \longrightarrow & 1\mbox{ h} \end{array} \)
La vitesse est donc \(7200\) m/h, c'est-à-dire 7,2 km/h.
- Une personne se déplaçant à une vitesse constante parcourt 2 km en 30 minutes.
- Quelle est sa vitesse ?
- Quelle distance parcourra-t-elle en 45 min ? en 75 min ?
Solution détaillée :
- Parcourir 2 km en 30 minutes, revient à faire 4 km en une heure. Sa vitesse est donc 4 km/h.
- Parcourir 2 km en 30 minutes, revient à faire 1 km en 15 minutes et donc 3 km en 45 minutes et 5 km en 75 minutes.
- Calculer la longueur de la diagonale du cube d'arête \(c\).
Solution détaillée :
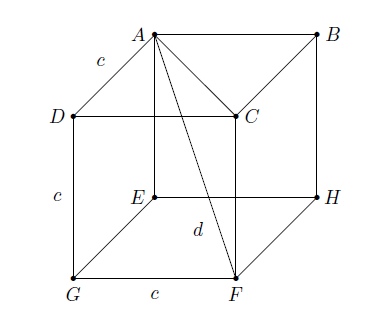
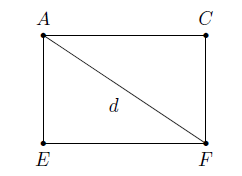
La diagonale du cube d'arête \(c\)est la diagonale du rectangle \(ACFE\) et est telle que
\(d^2=\vert AC\vert^2+\vert CF\vert^2=\vert AC\vert^2+c^2.\)
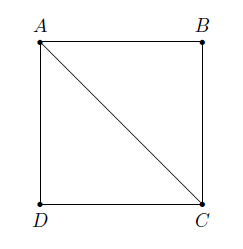
D'autre part, \(AC\) est la diagonale du carré \(ABCD\) et donc
\(\vert AC\vert^2=c^2+c^2=2c^2.\)
Finalement on obtient \(d^2=2c^2+c^2=3c^2\) et donc la longueur de la diagonale du cube est \(d=\sqrt{3}\, c\).
- Pour mesurer la hauteur d'un arbre, on place un bâton de \(1\) m de haut à \(10\) m de son tronc. En visant le sommet du bâton à \(2\) m de ce bâton, on constate qu'il est aligné avec le sommet de l'arbre. Déterminer la hauteur de cet arbre.
Solution détaillée : Nous pouvons représenter la situation par deux triangles rectangles emboîtés.
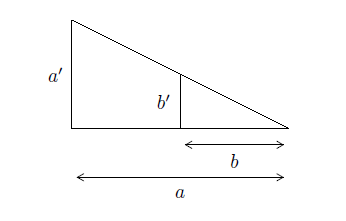
où \(a'\) représente la hauteur de l'arbre et \(b'\) celle du bâton. On a \(b=2\) m, \(b'=1\) m, \(a=2+10\) m et par Thalès
\(\dfrac{a'}{a}=\dfrac{b'}{b}\)
d'où \(a'=\frac{b'}{b}\cdot a=\frac{1}{2}\cdot 12=6\) m.
- Un pendule oscille au bout d'une corde de 50 cm. Sachant que l'angle décrit est de \(60^{\circ}\), trouver la longueur de l'arc décrit.
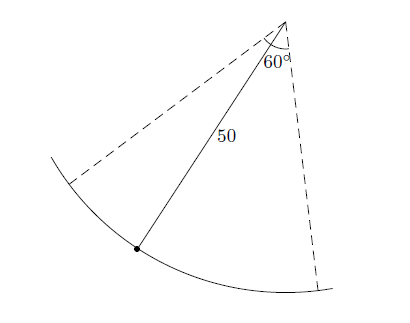
Solution détaillée :
On a \(r=50\) cm, \(\theta=60^{\circ}=\frac{\pi}{3}\) radians. Donc \(L=r\theta=50\cdot\frac{\pi}{3}\mbox{ cm}\).
- Que faire pour doubler le volume d'un parallélipipède rectangle ? Que devient son aire latérale ?
Solution détaillée : Pour doubler le volume d'un parallélipipède rectangle, il faut doubler une de ses dimensions, par exemple sa hauteur.
Si \(L\) représente la longueur de la base, \(l\)sa largeur et \(h\)la hauteur, l'aire latérale du parallélipipède de départ est donné par \(A=2(Ll+lh+Lh)\).
Si on double sa hauteur, cette aire latérale devient \(A'=2(Ll+2lh+2Lh)\).
- Etes-vous capable de porter un rouleau de fil de cuivre mesurant 100 m de long et 3 mm de diamètre, si 1 dm\(^3\) de cuivre pèse 8,9 kg ?
Solution détaillée : On a \(l=100\) m=\(100000\) mm, \(d=3\) mm et donc \(r=1,5\) mm. Le volume du rouleau est donné par
\(V=\pi\, r^2\, l=\pi\cdot (1,5)^2\cdot 100000=706858,3\mbox{ mm}^3=706,86\mbox{ cm}^3\approx 0,71\mbox{ dm}^3.\)
Puisque 1 dm\(^3\) pèse \(8,9\) kg, on en déduit que 0,711 dm\(^3\) pèsent \(0,71\cdot 8,9=6,3\) kg.
On peut donc le porter.
