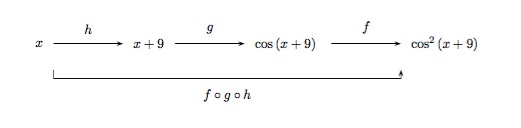Théorie du module : Fonctions

Opérations sur les fonctions

(a) Opérations arithmétiques

Tout comme on associe deux nombres réels dans l'addition, la soustraction, la multiplication ou la division, on peut assembler deux fonctions \(f\) et \(g\) pour former de nouvelles fonctions, \(f+g\), \(f-g\), \(f\cdot g\) et \(f/g\).

Par exemple, la fonction somme \(f+g\) est définie par

\((f+g)(x)=f(x)+g(x).\)

Le membre de droite n'a du sens que si \(f(x)\) et \(g(x)\) sont définies, autrement dit, si \(x\) appartient à la fois au domaine de définition de \(f\) et de \(g\). Si le domaine de définition de \(f\) est \(A\) et celui de \(g\) est \(B\), alors le domaine de \(f+g\) est leur intersection \(A\cap B\). Le signe \(+\) du membre de gauche désigne une addition de fonctions tandis que le signe \(+\) du membre de droite désigne une simple addition entre les nombres réels \(f(x)\) et \(g(x)\).

Nous pouvons définir de la même manière la fonction différence \(f-g\) et la fonction produit \(f\cdot g\) et leur domaine de définition est aussi \(A\cap B\). Au moment de définir la fonction quotient \(f/g\), nous devons nous souvenir de ne pas diviser par 0.

On considère les fonctions \(f(x)=\sqrt x\) et \(g(x)=\sqrt{4-x^2}\). Le domaine de définition de \(f(x)=\sqrt x\) est \([0;+\infty[\). Le domaine de définition de \(g(x)=\sqrt{4-x^2}\) comprend toutes les valeurs de \(x\) telles que \(4-x^2\ge 0\), c'est-à-dire \(-2\le x\le 2\). Le domaine de définition de \(g\) est donc l'intervalle \([-2,2]\). L'intersection des domaines de définition de \(f\) et \(g\) est

\([0;+\infty[\,\cap\,[-2,+2]=[0,2].\)

De là, suivant les définitions, nous avons

\(\begin{array}{llll} (f+g)(x)&=&\sqrt x+\sqrt{4-x^2}\quad &\mbox{pour }0\le x\le 2\\ (f-g)(x)&=&\sqrt x-\sqrt{4-x^2}\quad &\mbox{pour }0\le x\le 2\\ (f\cdot g)(x)&=&\sqrt x\sqrt{4-x^2}=\sqrt{4x-x^3}\quad &\mbox{pour }0\le x\le 2\\ \displaystyle \left(\frac fg\right)(x)&=&\displaystyle \frac{\sqrt x}{\sqrt{4-x^2}}=\sqrt{\frac{x}{4-x^2}}\quad &\mbox{pour }0\le x<2 \end{array}\)
 

Vous aurez remarqué que le domaine de définition de \(f/g\) est l'intervalle \([0,2[\) car il a fallu exclure les valeurs de \(x\) en lesquelles \(g(x)=0\), à savoir \(x=\pm 2\).

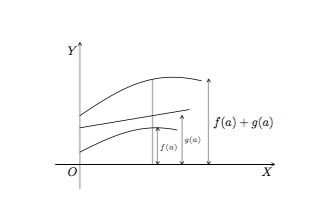
Le graphique de la fonction \(f+g\) s'obtient par addition graphique. Cela signifie que, pour chaque valeur de \(x\), nous additionnons les ordonnées correspondantes.

(b) Transformations de fonctions

En appliquant certaines transformations au graphique d'une fonction donnée, on obtient les graphiques de fonctions apparentées et on réduit ainsi fortement le travail nécessaire à la recherche de leur graphique.

Déplacements verticaux et horizontaux

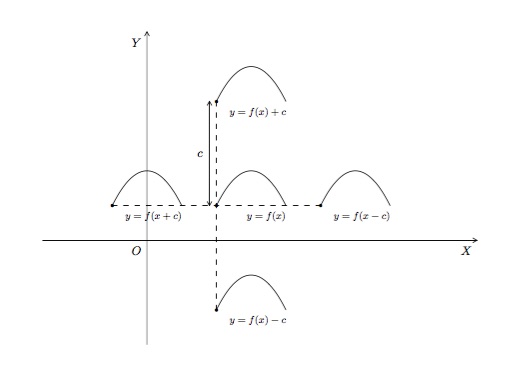
Considérons en premier lieu les translations. Si \(c\) est un nombre strictement positif, le graphique de \(y=f(x)+c\) est le même que celui de \(y=f(x)\) déplacé vers le haut de \(c\) unités (puisque chaque ordonnée \(y\) est augmentée de la même quantité \(c\)). De même, si \(g(x)=f(x-c)\) avec \(c>0\), la valeur de \(g\) en \(x\) est la même que la valeur de \(f\) en \(x-c\) (point situé \(c\) unités à gauche de \(x\)). De là, le graphique de \(g(x)=f(x-c)\) est le même que celui de \(y=f(x)\) déplacé de \(c\) unités vers la droite.

Etirements, compressions et réflexions 

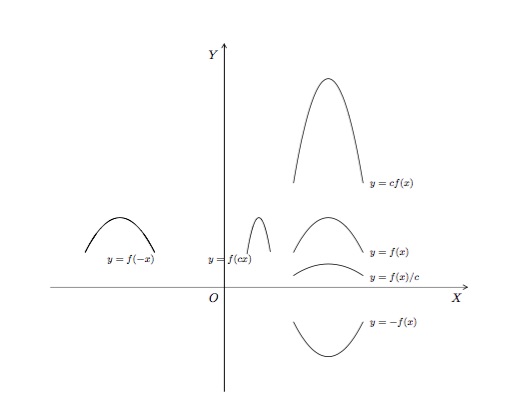
Si \(c>0\), alors le graphique de \(y=cf(x)\) est le graphique de \(y=f(x)\) étiré ou comprimé verticalement d'un facteur \(c\) (parce que chaque ordonnée \(y\) est multipliée par le même nombre \(c\)). Le graphique de \(y=-f(x)\) est le graphique de \(y=f(x)\) réfléchi par rapport à l'axe \(OX\) parce que le point \((x,y)\) est remplacé par le point \((x,-y)\).

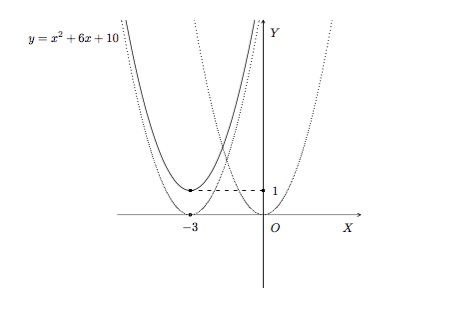
Dessinons la courbe représentative de la fonction \(f(x)=x^2+6x+10\). Le domaine de définition est \(\mathbb{R}\). En complétant le carré, nous écrivons l'équation de la courbe cherchée sous la forme

\(y=x^2+6x+10=(x+3)^2+1.\)

Dès lors, la courbe s'obtient en déplaçant la parabole \(y=x^2\) de 3 unités vers la gauche et de 1 unité vers le haut.

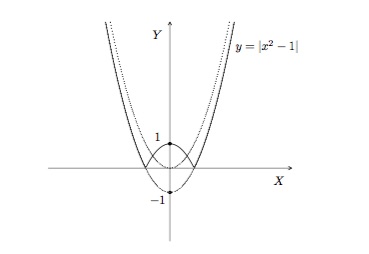
Dessinons la courbe représentative de \(y=|x^2-1|\). D'abord, nous traçons la parabole \(y=x^2-1\) en translatant d'une unité vers la bas la parabole \(y=x^2\). Nous pouvons voir qu'entre \(-1\) et \(1\) la courbe est sous l'axe \(OX\). Nous prenons l'image symétrique de cette partie par rapport à l'axe \(OX\) et laissons telle quelle le reste de la courbe. C'est le graphique de \(y=|x^2-1|\).

 

(c) Composition de fonctions

Une autre façon de créer de nouvelles fonctions est de les "composer'" entre elles. L'idée est d'appliquer des fonctions connues "en cascade", pour autant que les expressions ainsi obtenues aient toujours un sens.

Supposons, par exemple, que \(y=f(u)=\sqrt{u}\) et \(u=g(x)=x^2+1\). Comme \(y\) est une fonction de \(u\) et comme \(u\) est, à son tour, une fonction de \(x\), il s'ensuit que \(y\) est finalement une fonction de \(x\). Cette relation entre \(y\) et \(x\) se calcule par composition

\(y=f(u)=f(g(x))=f(x^2+1)=\sqrt{x^2+1}.\)

Cette opération s'appelle composition parce que la nouvelle fonction est composée des deux fonctions initiales \(f\) et \(g\).

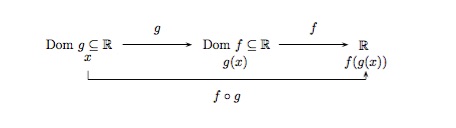
De façon générale, étant données deux fonctions \(f\) et \(g\), nous partons d'une valeur de \(x\) dans le domaine de définition de \(g\), nous calculons son image \(g(x)\). Si le nombre \(g(x)\) appartient au domaine de définition de \(f\), nous pouvons calculer la valeur \(f(g(x))\). Le résultat est une nouvelle fonction \(h(x)=f(g(x))\) obtenue en introduisant \(g\) dans \(f\). Elle s'appelle la "composée" de \(f\) et \(g\) et est notée \(f\circ g\) (\(f\) rond \(g\)).

Le domaine de définition de \(f\circ g\) est l'ensemble de toutes les valeurs de \(x\) du domaine de définition de \(g\) qui sont telles que \(g(x)\) appartient au domaine de définition de \(f\). Autrement dit, \(f\circ g\) est définie là où à la fois \(g(x)\) et \(f(g(x))\) sont définies. La meilleure image que l'on puisse donner de \(f\circ g\) est le diagramme suivant.

Si \(f(x)=x^2\) et \(g(x)=x-3\) alors on a

\((f\circ g)(x)=f(g(x))=f(x-3)=(x-3)^2,\)

\((g\circ f)(x)=g(f(x))=g(x^2)=x^2-3.\)

En général, \(f\circ g\ne g\circ f\). Souvenez-vous que la notation \(f\circ g\) signifie que la première fonction appliquée est \(g\) et la seconde \(f\). Ce qui, à l'exemple précédent, fait que pour appliquer \(f\circ g\), on soustrait d'abord 3, puis on élève au carré; alors que, pour appliquer \(g\circ f\), on devrait d'abord élever au carré, puis soustraire 3.

L'opération de composition s'applique aussi à trois fonctions ou davantage. Par exemple, la fonction composée \(f\circ g\circ h\) consiste à appliquer d'abord \(h\), ensuite \(g\) et finalement \(f\) :

\((f\circ g\circ h)(x)=f(g(h(x))).\)

Jusqu'à présent, par composition, nous avons construit des fonctions compliquées à partir de fonctions plus simples. Mais en analyse il est souvent utile ou nécessaire de décomposer une fonction compliquée en des fonctions plus simples.

Etant donnée la fonction \(F(x)=\cos^2(x+9)\), cherchons des fonctions \(f\), \(g\) et \(h\) telles que \(F=f\circ g\circ h\). La formule qui définit \(F\) dit : d'abord ajouter 9, puis prendre le cosinus du résultat, enfin, élever au carré. Ce qui fait que nous posons

\(h(x)=x+9,\quad g(x)=\cos x,\quad f(x)=x^2.\)

Effectivement

\(\begin{array} {lll}(f\circ g\circ h)(x)&=&f(g(h(x)))=f(g(x+9))=f(\cos(x+9))\\ &=&[\cos(x+9)]^2=F(x). \end{array}\)