Théorie du module : Repères et vecteurs
Table des matières
- Le plan \(\mathbb{R}^2\)
- L'espace \(\mathbb{R}^3\)
- La notion de vecteur
- Opérations sur les vecteurs
- Vecteurs et points particuliers
- Exemples détaillés
Le plan \(\mathbb{R}^2\)
(a) Repère
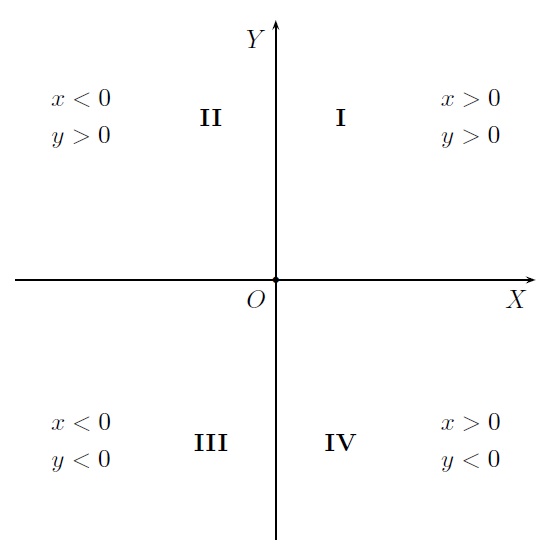
De même que l'on a identifié les points de la droite réelle (munie d'un repère : une origine et une longueur unité) aux nombres réels, on peut identifier les points du plan aux couples de nombres réels. Pour cela, il convient de se donner dans le plan un repère, constitué de deux droites sécantes, chacune munie d'une unité de longueur et qui se coupent en leur point origine. L'une des droites est appelée l'axe des \(x\)ou axe des abscisses, noté \(OX\), et l'autre est l'axe des \(y\)ou axe des ordonnées, noté \(OY\). En général, on utilise deux droites perpendiculaires, munies de la même unité de longueur. On parle alors de repère cartésien orthonormé. Le plan est ainsi divisé en quatre quadrants, le premier d'entre eux étant délimité par la partie positive des deux axes.
(b) Coordonnées cartésiennes
D'un point \(P\) quelconque du plan, on mène des parallèles aux axes qui coupent ceux-ci en \(a\) pour l'axe des \(x\) et en \(b\) pour l'axe des \(y\). Le point \(P\) est ainsi associé au couple de nombres réels \((a,b)\). Inversément, à tout couple de nombres réels \((a,b)\), en menant des parallèles aux axes passant par \(a\) porté sur l'axe des \(x\) et par \(b\) porté sur l'axe des \(y\), on fait correspondre l'unique point d'intersection de ces deux droites. Le couple \((a,b)\) est appelé coordonnées cartésiennes du point \(P\). Le nombre \(a\) est l'abscisse de \(P\) et le nombre \(b\) est son ordonnée.
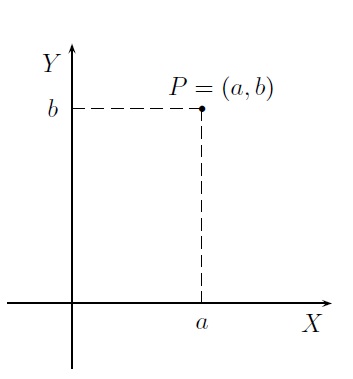
(c) Notion de distance
\(d(P,Q)= \sqrt{(x_q -x_p)^2 + (y_q-y_p)^2}.\)
Cette formule est une application immédiate du Théorème de Pythagore au triangle rectangle \(PQR\).
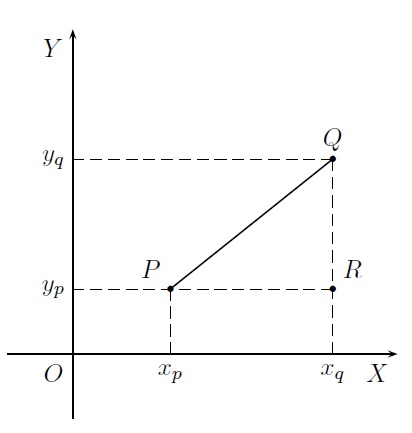
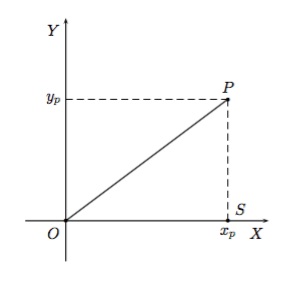
En particulier, la distance d'un point \(P=(x_p,y_p)\) à l'origine est donnée par \(\sqrt {x_p^2 +y_p^2}\) qui est la longueur de l'hypoténuse du triangle rectangle \(OPS\).
Application : Equation du cercle
Dans un plan fixé, on se donne un point \(C\) et un nombre \(r>0\).
\(d(P,C)=r.\)
Pour établir l'équation cartésienne du cercle, on se place dans un repère. Les coordonnées du point \(C\) dans ce repère sont \((x_c,y_c)\). Soit \(P=(x,y)\), un point du cercle. Puisque \(d(P,C)=r\), on a
\(\sqrt{(x-x_c)^2+(y-y_c)^2}=r.\)
\((x-x_c)^2+(y-y_c)^2=r^2.\)
En particulier, l'équation du cercle centré en \((0,0)\) et de rayon \(r\)} est\(x^2+y^2=r^2.\)
(d) Coordonnées polaires
Pour préciser la position d'un point \(P\), au lieu de ses coordonnées cartésiennes \((x,y)\), on peut donner les informations suivantes :
- la distance de \(P\) à l'origine, notée \(r\) (\(r>0\)),
- l'angle entre l'axe \(OX\) et \(OP\), noté \(\theta \). Par convention, \(\theta\in [0,2\pi[\, \).
Ce sont les coordonnées polaires du point \(P\).
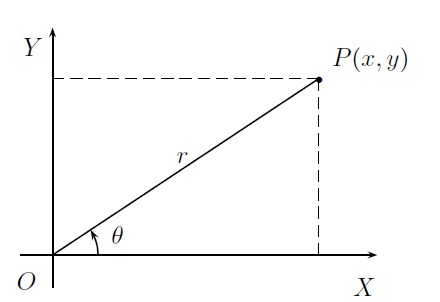
On observe immédiatement que
\(\left\{ \begin{array}{l} x = r \cos \theta\\ y = r \sin \theta \end{array}\right.\)
Le lien dans l'autre sens demande un peu plus d'attention. Vu que \(r\) est la distance de \(P\) à l'origine, on a
\(r =\sqrt{x^2 + y^2 }.\)
Pour \(\theta\), on note que si \(x = 0\) alors \(\theta = \frac{\pi}{2}\) ou \(\frac{3\pi}{2}\), selon que \(y > 0\) ou \(y < 0\). Si \(x \neq 0\), on a
\(\tan\theta=\frac{y}{x},\)
ce qui nous permet de trouver \(\theta\), en y ajoutant au besoin \(\pi\) selon les signes de \(x\) et \(y\).
Par exemple, pour \(P = (- \frac{\sqrt{3}}{2}, -\frac{1}{2})\) on trouve
\(r=\sqrt{\frac{3}{4}+\frac{1}{4}}=1\)
et
\(\arctan \frac{y}{x} = \arctan \frac{\sqrt{3}}{3} = \frac{\pi}{6}\)
et on doit prendre \(\theta = \frac{\pi}{6} + \pi=\frac{7\pi}{6}\) car les coordonnés cartésiennes de \(P\) sont toutes les deux négatives.
L'intérêt des coordonnées polaires est qu'elles permettent de décrire certaines figures géométriques à l'aide d'équations particulièrement simples. Voici quelques exemples :
Le cercle de centre \(O\) et de rayon \(R\) sera décrit par l'équation \(r = R\).
Une demi-droite issue de \(O\) et formant un angle \(\alpha\) avec l'axe \(OX\) sera décrite par \(\theta = \alpha\).
L'équation d'une ellipse en coordonnées polaires est
\(r = \frac{a - c^2/a }{1 + e \cos \theta}. \)
Cette description est utilisée en astronomie car la terre (ou une autre planète) décrit une ellipse dont un foyer est occupé par le soleil.
L'équation de la feuille de trèfle est donnée par \(r = \cos 3\theta \).
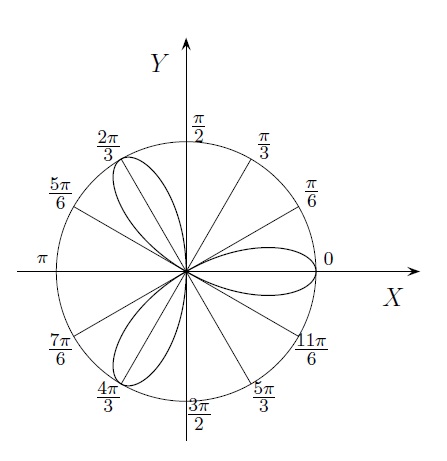
Si on essayait d'obtenir l'équation cartésienne correspondante, on pourrait utiliser le fait que \(\cos 3 \theta = \cos 2 \theta \cos \theta - \sin 2 \theta \sin \theta = \cos^3 \theta - 3 \sin^2\theta \cos \theta\) et en tirer la relation
\(r^4 = r^3\cos^3 \theta - 3 (r^2 \sin^2 \theta)(r\cos \theta)\)
ou encore
\((x^2 + y^2 )^2 = x^3 - 3x y^2.\)
Il n'est pas évident de voir l'allure de la courbe à partir de cette équation ! En coordonnées polaires, les choses sont plus simples.
