Théorie du module : Repères et vecteurs

Exemples détaillés

1. Déterminer les coordonnées polaires du point \(P=(-\frac{\sqrt{2}}{4},\frac{\sqrt{2}}{4})\)

Solution détaillée : On a

\(r=\sqrt{\left(-\frac{\sqrt{2}}{4}\right)^2+\left(\frac{\sqrt{2}}{4}\right)^2}=\sqrt{\frac{2}{16}+\frac{2}{16}}=\sqrt{\frac{1}{4}}=\frac{1}{2} \)

et

\(\tan{\theta}=\frac{\frac{\sqrt{2}}{4}}{-\frac{\sqrt{2}}{4}}=-1\)

donc \(\theta=\frac{3\pi}{4}\) ou \(\theta=\frac{7\pi}{4}\). Les coordonnées cartésiennes indiquent que le point \(P\) se trouve dans le deuxième quadrant et donc \(\theta=\frac{3\pi}{4}\).
Le point \(P\) en coordonnées polaires s'écrit donc \(P=(\frac{1}{2}\cos{(\frac{3\pi}{4})},\frac{1}{2}\sin{(\frac{3\pi}{4})})\).

2. Déterminer les coordonnées cartésiennes du point \(P\) si \(r=2\) et \(\theta=\frac{7\pi}{6}\).

Solution détaillée : On a

\(x=r\cos\theta=2\cos{\left(\frac{7\pi}{6}\right)}=2\cdot \left(-\frac{\sqrt{3}}{2}\right)=-\sqrt{3} \)

et

\(y=r\sin\theta=2\sin{\left(\frac{7\pi}{6}\right)}=2\cdot \left(-\frac{1}{2}\right)=-1.\)

Le point \(P\) a donc pour coordonnées cartésiennes \(P=(-\sqrt{3},-1)\).

3. Déterminer la distance entre les points \((3,1)\) et \((2,4)\).

Solution détaillée : On calcule \(d=\sqrt{(2-3)^2+(4-1)^2}=\sqrt{1+9}=\sqrt{10}\).

4. Donner l'équation du cercle de centre \((1,2)\) et passant par le point \((6,-1)\).

Solution détaillée : Le rayon de ce cercle est donné par la distance entre les points \((1,2)\) et \((6,-1)\). Ce rayon vaut donc \(r=\sqrt{(6-1)^2+(-1-2)^2}=\sqrt{25+9}=\sqrt{34}\).
Le cercle centré en \((1,2)\) et de rayon \(\sqrt{34}\) a pour équation

\((x-1)^2+(y-2)^2=34\)

ou encore

\(x^2-2x+y^2-4y=29.\)

5. Déterminer le centre et le rayon de la sphère d'équation \(x^2+y^2+z^2-12x+14y-8z+1=0\).

Solution détaillée : On a successivement

\(\begin{array}{l} x^2-12x+y^2+14y+z^2-8z=-1\\ x^2-2\cdot 6\cdot x+36+y^2+2\cdot 7\cdot y+49+z^2-2\cdot 4\cdot z+16=-1+36+49+16\\ (x-6)^2+(y+7)^2+(z-4)^2=100 \end{array}\)

Il s'agit donc d'une sphère de centre \((6,-7,4)\) et de rayon \(10\).

6. Déterminer \(\vec{a}+\vec{b}\), \(\vec{a}-\vec{b}\) et \((\vec{a}-4\vec{b})\) pour \(\vec{a}=(-2,6,1)\), \(\vec{b}=(3,-3,-1)\).

Solution détaillée : On a
\(\vec{a}+\vec{b}=(-2+3,6-3,1-1)=(1,3,0)\),
\(\vec{a}-\vec{b}=(-2-3,6-(-3),1-(-1))=(-5,9,2)\),
\((\vec{a}-4\vec{b})=(-2,6,1)-4(3,-3,-1)=(-2,6,1)-(12,-12,-4)=(-14,18,5)\).

7. Etant donné \(\vec{a}=(-2,3,1)\), \(\vec{b}=(7,4,5)\) et \(\vec{c}=(1,-5,2)\), calculer les nombres \(\vec{a}\odot \vec{b}\), \(\vec{a}\odot(\vec{b}+\vec{c})\) et \(\vec{a}\odot\vec{b}+\vec{a}\odot\vec{c}\).

Solution détaillée : On a
\(\vec{a}\odot \vec{b}=-2\cdot 7+3\cdot 4+1\cdot 5=-14+12+5=3\),
\(\vec{a}\odot(\vec{b}+\vec{c})=(-2,3,1)\odot (8,-1,7)=-2\cdot 8+3\cdot (-1)+1\cdot 7=-12\),
\(\vec{a}\odot\vec{b}+\vec{a}\odot\vec{c}=-2\cdot 7+3\cdot 4+1\cdot 5+(-2)\cdot 1+3\cdot (-5)+1\cdot 2=-12\).
Remarquons que \(\vec{a}\odot(\vec{b}+\vec{c})=\vec{a}\odot\vec{b}+\vec{a}\odot\vec{c}\).

8. Etant donné \(\vec{a}=(1,0,2)\), \(\vec{b}=(-1,2,1)\) et \(\vec{c}=(0,1,-1)\), calculer les vecteurs \((\vec{a}\times\vec{b})\times\vec{c}\) et \(\vec{a}\times(\vec{b}\times\vec{c})\).

   Solution détaillée : On a
   \(\vec{a}\times\vec{b}=(0\cdot 1-2\cdot 2,2\cdot (-1)-1\cdot 1,1\cdot 2-0\cdot (-1))=(-4,-3,2)\),
   \((\vec{a}\times\vec{b})\times\vec{c}=(-3\cdot (-1)-2\cdot 1,2\cdot 0-(-4)\cdot (-1),-4\cdot 1-(-3)\cdot 0)=(1,-4,-4)\).
   D'autre part,
   \(\vec{b}\times\vec{c}=(2\cdot (-1)-1\cdot 1,1\cdot 0-(-1)\cdot (-1),(-1)\cdot 1-0\cdot 2)=(-3,-1,-1)\),
   \(\vec{a}\times(\vec{b}\times\vec{c})=(0\cdot (-1)-2\cdot (-1),2\cdot (-3)-1\cdot (-1),1\cdot (-1)-0\cdot (-3))=(2,-5,-1)\).
   Remarquons que \((\vec{a}\times\vec{b})\times\vec{c}\neq\vec{a}\times(\vec{b}\times\vec{c})\).

9. Déterminer si \(\vec{a}=(4,-1,-2)\) et \(\vec{b}=(2,-2,5)\) sont orthogonaux.

   Solution détaillée : On sait que \(\vec{a}\perp\vec{b}\Leftrightarrow \vec{a}\odot\vec{b}=0\).
   On calcule \(\vec{a}\odot\vec{b}=4\cdot 2+(-1)\cdot (-2)+(-2)\cdot 5=0\), donc les vecteurs \(\vec{a}\) et \(\vec{b}\) sont orthogonaux.

10. Déterminer les valeurs de \(c\) pour que les vecteurs \(\vec{a}=(c,-2,3)\) et \(\vec{b}=(c,c,-5)\) soient orthogonaux.

    Solution détaillée : On sait que \(\vec{a}\perp\vec{b}\Leftrightarrow \vec{a}\odot\vec{b}=0\).
    Or \(\vec{a}\odot\vec{b}=c^2-2c-15\) et donc

    \(\begin{array}{rcl} \vec{a}\odot\vec{b}=0&\Leftrightarrow &c^2-2c-15=0, \\ &\Leftrightarrow &(c-5)(c+3)=0, \\ &\Leftrightarrow & c=5\mbox{ ou }c=-3. \end{array} \)

    Pour plus de détails sur la factorisation, cliquez ici.

11. Soit \(P_1=(-1,2,3)\) et \(P_2=(2,-2,8)\). Donner les composantes du vecteur \(\overrightarrow{P_1P_2}\), sa longueur et les coordonnées du point M, milieu de \(\overrightarrow{P_1P_2}\). Déterminer aussi les coordonnées de \(P_3\) tel que \(\overrightarrow{P_1P_3}=3\, \overrightarrow{P_1P_2}\).

    Solution détaillée : On a
    \(\overrightarrow{P_1P_2}=(2-(-1),-2-2,8-3)=(3,-4,5\),
    \(\|\overrightarrow{P_1P_2}\|=\sqrt{3^2+(-4)^2+5^2}=\sqrt{9+16+25}=\sqrt{50}=5\sqrt{2}\),
    \(M=\frac{P_1+P_2}{2}=\frac{1}{2}(-1+2,2-2,3+8)=(\frac{1}{2},0,\frac{11}{2})\).
    Soit \(P_3=(a,b,c)\). On a \(\overrightarrow{P_1P_3}=P_3-P_1=(a+1,b-2,c-3)\) et \(\overrightarrow{P_1P_2}=P_2-P_1=(2+1,-2-2,8-3)=(3,-4,5)\). Il faut donc que \(a+1=3\cdot 3=9\), \(b-2=3\cdot (-4)=-12\) et \(c-3=3\cdot 5=15\). Donc \(a=8\), \(b=-10\), \(c=18\) et \(P_3=(8,-10,18)\).

12. Le point \(P\) est soumis à deux forces \(\overrightarrow{PQ}\) et \(\overrightarrow{PR}\) d'intensités respectives de 5N et 8N (le Newton est l'unité de force). La direction de \(\overrightarrow{PQ}\) est N\(20^\circ\)E et la direction de \(\overrightarrow{PR}\) est N\(65^\circ\)O. Donner les composantes horizontales et verticales de \(\overrightarrow{PQ}\) et \(\overrightarrow{PR}\).

    Solution détaillée : On peut repésenter la situation à l'aide du schéma suivant :

    

    On a \(\|\overrightarrow{PQ} \|=5\) et \(\|\overrightarrow{PR} \|=8\). Soit \((a,b)\) les composantes de \(\overrightarrow{PQ}\) et \((c,d)\), les composantes de \(\overrightarrow{PR}\).
    On calcule \(a=\|\overrightarrow{PQ} \|\, \cos{(90^{\circ}-20^{\circ})}=5\cos{70^{\circ}}\) et \(b=\|\overrightarrow{PQ} \|\, \sin{(90^{\circ}-20^{\circ})}=5\sin{70^{\circ}}\). La composante horizontale de \(\overrightarrow{PQ}\) est \(a=5\cos{70^{\circ}}\) et la composante verticale de \(\overrightarrow{PQ}\) est \(b=5\sin{70^{\circ}}\).
    De même, \(c=-\|\overrightarrow{PR} \|\, \cos{(90^{\circ}-65^{\circ})}=-8\cos{25^{\circ}}\) et \(d=\|\overrightarrow{PR} \|\, \sin{(90^{\circ}-65^{\circ})}=8\sin{25^{\circ}}\). La composante horizontale de \(\overrightarrow{PR}\) est \(c=-8\cos{25^{\circ}}\) et la composante verticale de \(\overrightarrow{PR}\) est \(d=8\sin{25^{\circ}}\).

13. Deux forces \(\vec{F_1}\) et \(\vec{F_2}\) qui agissent simultanément sur un point matériel \(P\) ont une action équivalente à une force unique appelée résultante \(\vec{R}\). Cette résultante est obtenue en traçant la diagonale du parallélogramme construit sur les vecteurs \(\vec{F_1}\) et \(\vec{F_2}\).

    

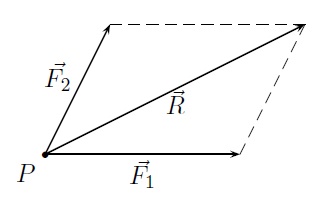
    Dans la construction de la résultante, il suffit de tracer la moitié du parallélogramme où l'on place bout à bout les vecteurs \(\vec{F_1}\) et \(\vec{F_2}\). On a \(\vec{R}=\vec{F_1}+\vec{F_2}\).

    

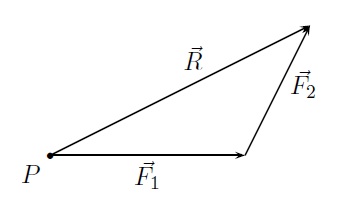
14. L'intensité et la direction d'une force constante sont données par \(\overrightarrow{a}= (2,5)\). Calculer le travail effectué si le point d'application de la force se déplace de l'origine au point \(P=(4,1)\).

    Solution détaillée : Si \(\vec{F}\) est une force constante et \(\vec{d}\) représente le déplacement, on a \(W=\vec{F}\odot\vec{d}\). Ici, \(\vec{F}=\vec{a}=(2,5)\), \(\vec{d}=\overrightarrow{OP}= (4,1)\) et donc \(W=\vec{F}\odot\vec{d}=2\cdot 4+5\cdot 1=13\) Joules.

15. Sur un plan incliné dont la pente fait un angle de \(30^{\circ}\) avec l'horizontale, on pousse vers le haut un petit wagonnet pesant 500 N. Calculer le travail effectué pour compenser la force de gravitation si l'on pousse le wagonnet sur une distance de 24 m.

    Solution détaillée : Représentons schématiquement le problème dans un système de coordonnées :

    

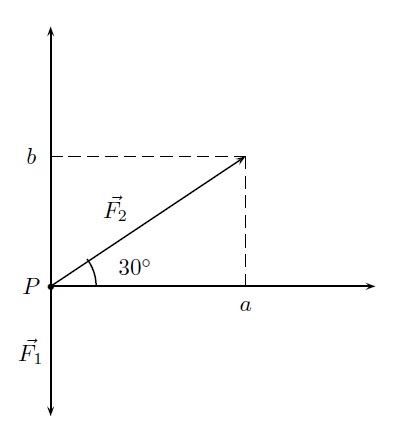
    Le vecteur \(\vec{F_1}=(0,-500)\) représente la force de gravitation orientée vers le bas d'une intensité de 500 N. Le point d'application de cette force se déplace le long du vecteur \(\vec{F_2}\) de norme 24. Les composantes de ce vecteur sont \(a=\|\vec{F_2}\|\, \cos{30^{\circ}}= 24\cdot\frac{\sqrt{3}}{2}= 12\sqrt{3}\) et \(b=\|\vec{F_2}\|\, \sin{30^{\circ}}=24\cdot\frac{1}{2}= 12\). Donc \(\vec{F_2}=(12\sqrt{3},12)\) et \(W=\vec{F_1}\odot\vec{F_2}= (0,-500)\odot(12\sqrt{3}, 12) =-6000\). Le travail effectué pour compenser la force de gravitation est donc de 6000 Joules.