Théorie du module : Trigonométrie

Table des matières

Angles

(a) Définitions

Définition - Un angle est une portion du plan comprise entre deux demi-droites. Il est composé de deux côtés ayant un même sommet. Si \(O\) est le sommet et \(A\), \(B\) sont deux

points sur les côtés, on parlera de l'angle \(\widehat{AOB}\).

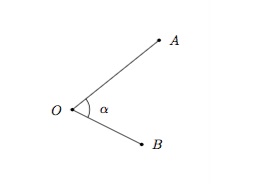
Un angle est souvent désigné par une lettre grecque minuscule telle \(\alpha\), \(\beta\), \(\gamma\) ou \(\theta\).

La mesure d'un angle s'exprime soit en degrés, soit en radians. Un angle de \(1\) degré correspond à \(\frac{1}{360}\) d'une rotation d'un tour complet dans le sens inverse des aiguilles d'une montre. La mesure d'un angle \(\alpha\), ou amplitude de l'angle, est la mesure de longueur \(s\) de l'arc \(AB\) (où \(A\) et \(B\) se trouvent sur le cercle unité centré en \(O\)).

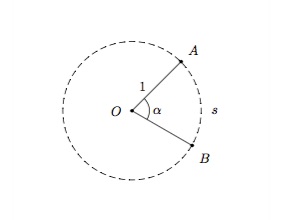
Lorsque \(s=1\), on dira que \(\alpha\) mesure \(1\) radian. Puisque la longueur du cercle unité est \(2\pi\), on obtient la correspondance suivante entre degrés et radians :

\begin{array}{c} 360^\circ=2\pi\mbox{ radians }\\ 1\mbox{ radian } = \displaystyle\frac{360^\circ}{2 \pi}= 57^\circ 17' 45''\dots \\ 1\mbox{ degré }= \displaystyle\frac{2 \pi }{360}\mbox{ radians } = 0,01745 \mbox{ radians} \end{array}

Un angle est aigu si son amplitude est inférieure à \(90^{\circ}\). Un angle droit est un angle dont l'amplitude est \(90^{\circ}\). Un angle est obtu si son amplitude est entre \(90^{\circ}\) et \(180^{\circ}\). Un angle plat est un angle dont l'amplitude est \(180^{\circ}\).

Deux angles ayant même amplitude sont dits congruents. Deux angles sont équivalents si la différence d'amplitude de ces angles est un multiple de \(360^\circ = 2\pi\) radians.

Des angles sont complémentaires si la somme de leurs amplitudes vaut \(90^{\circ}\). Des angles sont supplémentaires si la somme de leurs amplitudes vaut \(180^{\circ}\). Deux angles dont la différence des amplitudes vaut \(180^\circ\) sont dits anti-supplémentaires. Deux angles sont opposés si la somme de leurs amplitudes vaut \(0^{\circ}\).

Par exemple, si l'angle \(\alpha=30^{\circ}\) alors l'angle \(60^{\circ}\) est le complémentaire de \(\alpha\), l'angle \(150^{\circ}\) est le supplémentaire de \(\alpha\), l'angle \(210^{\circ}\) est l'anti-supplémentaire de \(\alpha\). L'angle \(-30^{\circ}\) est l'opposé de \(\alpha\) et l'angle \(750^{\circ}\) est équivalent à \(\alpha\).

(b) Positions relatives de deux angles

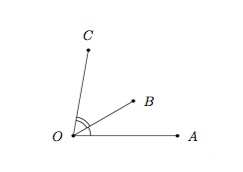
Deux angles sont adjacents s'ils ont le même sommet et un côté commun. Dans la figure ci-dessous, les angles \(\widehat{AOB}\) et \(\widehat{BOC}\) sont adjacents.

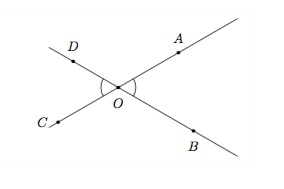
Deux angles sont opposés par le sommet s'ils ont même sommet et si leurs côtés sont les prolongements respectifs l'un de l'autre. Dans la figure ci-dessous, les angles \(\widehat{AOB}\) et \(\widehat{DOC}\) sont opposés par le sommet, ainsi que les angles \(\widehat{AOD}\) et \(\widehat{BOC}\).

Propriété - Deux angles opposés par le sommet ont même amplitude.

Considérons deux droites parallèles \(d_1\) et \(d_2\) coupées par une droite \(d_3\). Soit \(A\) le point d'intersection de \(d_1\) et \(d_3\) et \(B\) le point d'intersection de \(d_2\) et \(d_3\).

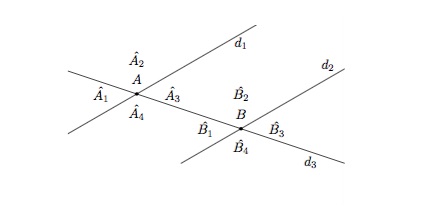
Deux angles sont correspondants s'ils n'ont pas le même sommet et se trouvent du même côté de la droite \(d_3\) et du même côté respectivement de la droite \(d_1\) et de la droite \(d_2\).

Par exemple, les angles \(\widehat{A_1}\) et \(\widehat{B_1}\) sont correspondants, les angles \(\widehat{A_2}\) et \(\widehat{B_2}\) sont correspondants, les angles \(\widehat{A_3}\) et \(\widehat{B_3}\) sont correspondants et les angles \(\widehat{A_4}\) et \(\widehat{B_4}\) sont correspondants.

Deux angles sont alternes internes s'ils n'ont pas le même sommet et se trouvent de part et d'autre de la droite \(d_3\) et entre les droites \(d_1\) et \(d_2\).

Par exemple, les angles \(\widehat{A_4}\) et \(\widehat{B_2}\) sont alternes internes. Et les angles \(\widehat{A_3}\) et \(\widehat{B_1}\) sont alternes internes.

Deux angles sont alternes externes s'ils n'ont pas le même sommet et se trouvent de part et d'autre de la droite \(d_3\) et à l'extérieur des droites \(d_1\) et \(d_2\).

Par exemple, les angles \(\widehat{A_1}\) et \(\widehat{B_3}\) sont alternes externes. Et les angles \(\widehat{A_2}\) et \(\widehat{B_4}\) sont alternes externes.

Propriétés

Deux angles correspondants ont même amplitude.

Deux angles alternes internes ont même amplitude.

Deux angles alternes externes ont même amplitude.

(c) Angles et cercles

On considère un cercle de centre \(O\) et \(A\), \(B\), \(C\) trois points de ce cercle.

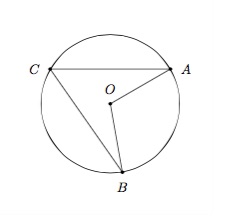
Un angle est inscrit dans un cercle si son sommet est un point du cercle et si ses deux côtés coupent le cercle en un deuxième point.

Par exemple, dans la figure ci-dessus, l'angle \(\widehat{ACB}\) est inscrit dans le cercle. Cet angle intercepte l'arc \(AB\).

Propriété - Dans un cercle, des angles inscrits interceptant le même arc ont même amplitude.

Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.

Dans le cas particulier où l'angle inscrit dans un cercle intercepte un diamètre, on a le résultat suivant.

Propriété - Tout triangle inscrit dans un demi-cercle est un triangle rectangle. Réciproquement, on peut inscrire tout triangle rectangle dans un demi-cercle dont le diamètre est l'hypoténuse du triangle.

Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.

Un angle au centre d'un cercle a le centre de ce cercle comme sommet.

Par exemple, dans la figure ci-dessus, l'angle \(\widehat{AOB}\) est un angle au centre. Cet angle intercepte l'arc \(AB\).

Propriété - Dans un cercle, l'amplitude de l'angle au centre vaut le double de l'amplitude de l'angle inscrit qui intercepte le même arc.

Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.

Par exemple, dans la figure ci-dessus, l'amplitude de l'angle \(\widehat{AOB}\) vaut le double de l'amplitude de l'angle \(\widehat{ACB}\).

Théorie

Retour au module