Théorie du module : Logarithmes et exponentielles
Table des matières
Afficher toute la théorie du moduleLe logarithme naturel
Les fonctions logarithmiques et exponentielles peuvent être définies de plusieurs manières. Ici, on part du logarithme naturel (également appelé logarithme népérien), que l'on définit à l'aide d'une primitive. On en déduit les propriétés de ce logarithme ainsi que les autres fonctions logarithmiques et les fonctions exponentielles.
(a) Définition
Nous cherchons une fonction \(f\) :
- dérivable,
- qui satisfait la condition \(f(xy)=f(x)+f(y)\).
Ces exigences imposent à la fonction que \(f(1)=0\) et qu'elle doit satisfaire à la propriété
\(f'(x)=\dfrac{c}{x},\)
pour \(x\neq 0\) et \(c=f'(1)\). En effet,
\(f(1)=f(1\cdot 1)=f(1)+f(1)=2f(1)\)
Ceci n'est possible que si \(f(1)=0\).
Nous pouvons donc conclure que \(f(x)\) sera une primitive de \(\dfrac{c}{x}\). Nous choisissons \(c=1\) et tenons compte du fait que \(f(1)=0\). Cela nous mène à la définition suivante.
\(\ln:\mathbb{R}^+_0\to\mathbb{R}:x\mapsto\ln x=\displaystyle\int_1^x\dfrac{1}{t}\,dt.\)
Le logarithme représente donc la surface sous la courbe de la fonction \(\dfrac{1}{t}\) de \(t=1\) à \(t=x\), comme on le voit sur la figure suivante
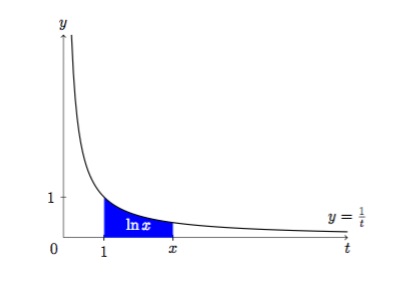
Figure 1 : La fonction \(\displaystyle\dfrac{1}{t}\) pour \(t>0\). La surface bleue donne la valeur de \(\ln x\).
Cette fonction est bien définie pour \(x>0\), car la fonction \(\displaystyle\dfrac{1}{t}\) est continue pour \(t>0\).
Le logarithme n'est par contre pas défini pour \(x<0\). En effet, l'intégrale \(\displaystyle\int_1^x\dfrac{1}{t}\, dt\) n'est pas bien définie pour \(x<0\) car l'intervalle \([x,1]\), sur lequel on intègre contient \(0\) et la fonction \(\displaystyle\dfrac{1}{t}\) n'est pas définie en \(0\), comme on peut le voir sur la Figure 2.
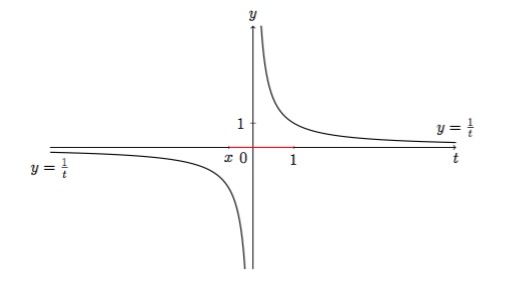
Figure 2 : La fonction \(\displaystyle\dfrac{1}{t}\). L'intervalle en rouge est l'intervalle sur lequel on devrait intégrer cette fonction pour obtenir \(\ln x\) si \(x<0\).
(b) Propriétés
Voici des propriétés importantes du logarithme naturel.
Propriétés :
- La fonction \(\ln x\) est dérivable pour tout \(x>0\) et sa dérivée est \(\dfrac{1}{x}\).
- La fonction \(\ln |x|\) est une primitive de \(\dfrac{1}{x}\) pour tout \(x\neq 0\) (aussi pour \(x<0\)).
Ces résultats sont une conséquence immédiate de la définition de \(\ln\).
Propriétés : Pour tout \(x,y>0\) et pour tout \(p\in\mathbb{Q}\), on a
- \(\ln (xy)=\ln x+\ln y\)
- \(\ln x^p=p\ln x\)
- \(\ln 1=0\)
- \(\displaystyle\ln \dfrac{1}{x}=-\ln x\)
- Si \(x>1\), alors \(\ln x>0\), si \(0<x<1\), alors \(\ln x<0\).
Les preuves de ces propriétés découlent de la définition :
- On a
\(\ln (xy)=\displaystyle\int_1^{xy}\dfrac{1}{t}\, dt=\underbrace{\displaystyle\int_1^x\dfrac{1}{t}\, dt}_{\ln x}+\displaystyle\int_x^{xy}\dfrac{1}{t}\, dt=\ln x+\displaystyle\int_x^{xy}\dfrac{\dfrac{1}{x}}{\dfrac{t}{x}}\, dt.\)
En effectuant la substitution \(s=\dfrac{t}{x}\), nous avons \(t\in[x,xy]\) d'où \(s=\dfrac{t}{x}\in[1,y]\) et donc
\(\ln(xy)=\ln x+\displaystyle\int_1^y\dfrac{1}{s}\, ds=\ln x+\ln y.\)
- En utlisant la Propriété 3, on a pour \(p\in\mathbb{N}\) :
- Si \(p=0\), alors \(\ln x^0=\ln 1=0=0\cdot \ln x\).
- Si \(p\geq 1\), alors
\(\ln x^p=\ln(\underbrace{x\cdot x\cdots x}_{p\text{ facteurs}})=\underbrace{\ln x+\ln x+\cdots+\ln x}_{p\text{ termes}}=p\ln x.\)
Par exemple, on a
\(\ln 6=\ln(3\cdot 2)=\ln 3+\ln 2,\)
\(\ln 8=\ln 2^3=3\ln 2\)
\(\ln \sqrt{2}=\ln 2^{1/2}=\dfrac{1}{2}\ln 2 \)
- La définition nous donne
\(\ln 1=\displaystyle\int_1^1\dfrac{1}{t}\, dt=0.\)
- Ce résultat ainsi que la Propriété 3 nous permet de conclure que
\(\ln\dfrac{1}{x}+\ln x=\ln\left(\dfrac{1}{x}\cdot x\right)=\ln 1=0.\)
Nous avons donc que \(\displaystyle\ln\dfrac{1}{x}+\ln x=0\), ce qui est équivalent à \(\displaystyle\ln\dfrac{1}{x}=-\ln x\).
- Pour \(x>1\), on a par la définition
\(\ln x=\displaystyle\int_1^x\dfrac{1}{t}\, dt.\)
Vu que nous intégrons une fonction positive et que la borne supérieure de l'intégrale (\(x\)) est plus grande que la borne inférieure (1), l'intégrale sera donc positive.
Si \(x<1\), on a que \(\dfrac{1}{x}>1\). La Propriété 6 nous permet de conclure que
\(\ln x=-\underbrace{\ln\dfrac{1}{x}}_{>0}<0.\)
Par exemple, on a
\(\ln 2 >0,\mbox{ mais }\displaystyle\ln\dfrac{1}{2}=-\ln 2<0.\)
\(y\in\mathbb R\), il existe exactement un \(x\in\mathbb R^+_0\) tel que \(y=\ln x\).
Proposition - Il existe exactement un nombre, que l'on nomme \(e\), tel que \(\ln e=1\).
Ce nombre \(e\) est irrationnel et \(e=2.71828\dots\)
(c) Représentation graphique de ln x
Nous allons maintenant analyser le comportement de la fonction \(\ln\). Nous savons déjà plusieurs choses utiles pour cette analyse :
- le domaine de \(\ln\) est \(\mathbb R^+_0\),
- la dérivée: \(\displaystyle(\ln x)'=\dfrac{1}{x}\),
- des valeurs particulières : \(\ln 1=0\) et \(\ln e=1\),
- le signe : \(\ln x<0\) si \(0<x<1\), et \(\ln x>0\) si \(x>1\).
Voici quelques propriétés supplémentaires.
Propriétés : La fonction \(\ln{x}\) possède les propriétés suivantes :
- La fonction \(\ln{x}\) est strictement croissante sur tout son domaine.
- La fonction \(\ln{x}\) est concave sur tout son domaine.
- Le graphique de la fonction \(\ln{x}\) a comme asymptote verticale \(x=0\).
- Le graphique de la fonction \(\ln{x}\) n'a pas d'asymptote horizontale.
- Le graphique de \(\ln{x}\) n'a pas d'asymptote oblique.
Si vous êtes intéressé, vous pouvez regarder la preuve de ces propriétés.
La fonction \(\ln{x}\) étant strictement croissante et concave sur tout son domaine, elle n'a ni extremum, ni point d'inflexion.
Résumons ce que nous savons de cette fonction dans un tableau :
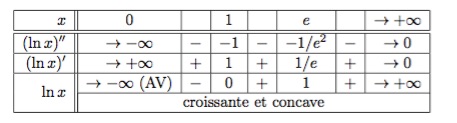
Ceci nous permet d'obtenir le graphique suivant :
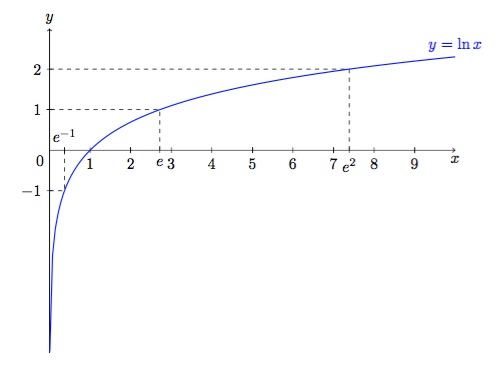
Figure 3 : Graphique de \(\ln x \).
