Théorie du module : Trigonométrie
Table des matières
- Angles
- Nombres trigonométriques
- Règle des sinus et Règle des cosinus
- Equations trigonométriques
- Exemples détaillés
Nombres trigonométriques
(a) Définition des nombres trigonométriques
Le cercle trigonométrique est un cercle de rayon 1 centré à l'origine. On mesure l'angle \(\alpha\) à partir de l'axe horizontal; \(\alpha\) est positif dans le sens anti-horlogique et négatif dans le sens des aiguilles d'une montre. Les angles sont définis à \(2\pi\) près; ainsi l'angle \(\alpha\) est le même que les angles \(\alpha+2\pi\) , \(\alpha+4\pi\) , \(\alpha-2\pi\) , \(\ldots\) , \(\alpha+2k\pi\) , \(k\in \mathbb{Z}\) .
Les nombres trigonométriques sinus et cosinus, tangente et cotangente sont définis pour un angle \(\alpha\) donné comme le montre la figure suivante.
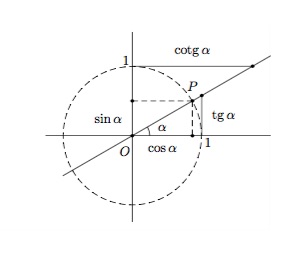
Définitions - Soit \(P\) un point du cercle trigonométrique faisant un angle \(\alpha\) avec l'axe horizontal. L'abscisse de \(P\) est appelée cosinus \(\alpha\) et l'ordonnée de \(P\) est appelée sinus \(\alpha\).
L'ordonnée du point d'abscisse \(1\) de la droite \(OP\) est appelée tangente \(\alpha\) et l'abscisse du point d'ordonnée \(1\) de la droite \(OP\) est appelée cotangente \(\alpha\).
Les coordonnées du point \(P\) sont donc \((\cos\alpha,\sin\alpha)\) et on a toujours
\begin{array}[t]{c} -1\leq\cos\alpha\leq 1\mbox{ et }-1\leq\sin\alpha\leq 1 \end{array}
On déduit du Théorème de Pythagore la formule fondamentale suivante :
\(\sin^2\alpha+\cos^2\alpha=1\)
Considérons les triangles rectangles \(OAB\) et \(OA'B'\).
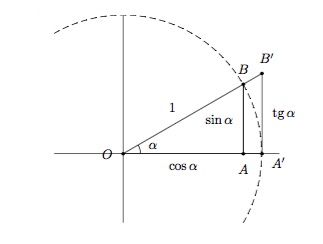
Ces deux triangles sont semblables et par les propriétés des triangles semblables, on a donc
\(tg\,\alpha=\frac{\sin\alpha}{\cos\alpha}.\)
Remarquons que le nombre \(tg\,\alpha\) n'est défini que pour \(\alpha\neq\frac{\pi}{2}+k\pi\), \(k\in \mathbb{Z}\). De même, on a
\(cotg\,\alpha=\frac{\cos\alpha}{\sin\alpha}=\frac{1}{tg\, \alpha},\)
où \(\alpha\neq k\pi\), \(k\in \mathbb{Z}\).
Toujours en utilisant les propriétés des triangles semblables, on a
\(\displaystyle\frac{|AB|}{|OB|}=\frac{|AB|}{1}=\sin\alpha,\)
d'où
\(\begin{array}[t]{c} \sin\alpha=\displaystyle\frac{\mbox{côté opposé à }\alpha}{\mbox{hypoténuse}}. \end{array}\)
De même, on a
\(\displaystyle\frac{|OA|}{|OB|}=\frac{|OA|}{1}=\cos\alpha, \)
d'où
\(\begin{array}[t]{c} \cos\alpha=\displaystyle\frac{\mbox{côté adjacent à }\alpha}{\mbox{hypoténuse}}. \end{array}\)
On en déduit que
\(\begin{array}[t]{c} tg\,\alpha=\displaystyle\frac{\sin\alpha}{\cos\alpha}=\frac{\mbox{côté opposé à }\alpha}{\mbox{côté adjacent à }\alpha}. \end{array}\)
Par exemple, si \(\alpha\) est un angle aigu et \(\cos \alpha = \frac{3}{4}\), on peut calculer les valeurs des nombres trigonométriques de \(\alpha\). Commençons par dessiner un triangle rectangle ayant un angle aigu \(\alpha\) avec "côté adjacent" =3 et "hypoténuse" =4.
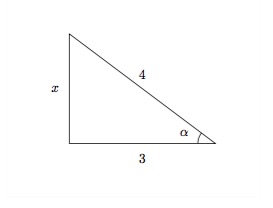
Soit \(x\) le côté opposé à \(\alpha\). Par le Théorème de Pythagore, on a
\(3^2 + x^2 = 4^2,\)
d'où \(x = \sqrt{16-9} = \sqrt{7}\). On en déduit
\(\begin{array}{ll} \sin \alpha = \frac{\mbox{opposé}}{\mbox{hypoténuse}}=\displaystyle\frac{\sqrt{7}}{4},&\hspace{3cm} tg\, \alpha = \frac{\mbox{opposé}}{\mbox{adjacent}}=\displaystyle\frac{\sqrt{7}}{3},\\[2mm] \cos \alpha = \frac{\mbox{adjacent}}{\mbox{hypoténuse}}=\displaystyle\frac{3}{4},&\hspace{3cm} cotg\, \alpha = \frac{\mbox{adjacent}}{\mbox{opposé}}=\displaystyle\frac{3}{\sqrt{7}}=\frac{3\sqrt{7}}{7}. \end{array}\)
Voici quelques valeurs remarquables des nombres trigonométriques.
\(\begin{array}{c|cccccc} \alpha&\hspace{4mm}0&\hspace{4mm}\displaystyle\frac{\pi}{6}&\hspace{4mm}\displaystyle\frac{\pi}{4}&\hspace{4mm}\displaystyle\frac{\pi}{3} &\hspace{4mm}\displaystyle\frac{\pi}{2}&\hspace{4mm}\pi\\[2mm] \hline \sin\alpha\hspace{2mm}&\hspace{4mm}0&\hspace{4mm}\displaystyle\frac{1}{2}&\hspace{4mm}\displaystyle\frac{\sqrt{2}}{2} &\hspace{4mm}\displaystyle\frac{\sqrt{3}}{2}&\hspace{4mm}1&\hspace{4mm}0\\[2mm] \cos\alpha\hspace{2mm}&\hspace{4mm}1&\hspace{4mm}\displaystyle\frac{\sqrt{3}}{2}&\hspace{4mm}\displaystyle\frac{\sqrt{2}}{2} &\hspace{4mm}\displaystyle\frac{1}{2}&\hspace{4mm}0&\hspace{4mm}-1\\[2mm] tg\,\alpha\hspace{2mm}&\hspace{4mm}0&\hspace{4mm}\displaystyle\frac{\sqrt{3}}{3}&\hspace{4mm}1&\hspace{4mm}\sqrt{3} &\hspace{4mm}/&\hspace{4mm}0 \end{array}\)
(b) Propriétés des nombres trigonométriques
Le calcul d'un nombre trigonométrique d'un angle donné peut se ramener au calcul d'un nombre trigonométrique d'un angle du premier quadrant. A partir des valeurs données dans la table ci-dessus, on peut déduire les valeurs d'autres nombres trigonométriques grâce aux formules ci-dessous.
Pour des angles opposés \(\alpha\) et \(-\alpha\)
Dans un cercle trigonométrique, deux angles opposés sont représentés par deux points du cercle symétriques par rapport à l'axe \(OX\).
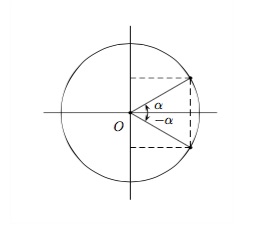
\(\begin{array}{ll} \sin ( -\alpha) = - \sin \alpha\hspace{2cm}&tg\,( -\alpha) = - tg\,\alpha\\ \cos ( -\alpha) = \cos \alpha&cotg\,( -\alpha) = - cotg\,\alpha \end{array}\)
Pour des angles complémentaires \(\alpha\) et \({\pi \over 2} -\alpha\)
Dans un cercle trigonométrique, deux angles complémentaires sont représentés par deux points du cercle symétriques par rapport à la droite \(y=x\).
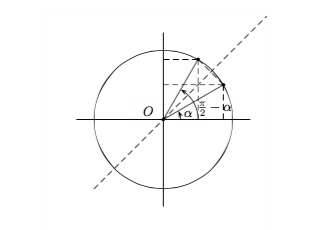
\(\begin{array}{ll} \sin ({\pi \over 2} -\alpha) = \cos \alpha\hspace{2cm}&tg\,({\pi \over 2} -\alpha) = cotg\, \alpha\\ \cos ({\pi \over 2} -\alpha) = \sin \alpha&cotg\,({\pi \over 2} -\alpha) = tg\,\alpha \end{array}\)
Pour des angles supplémentaires \(\alpha\) et \(\pi -\alpha\)
Dans un cercle trigonométrique, deux angles supplémentaires sont représentés par deux points du cercle symétriques par rapport à l'axe \(OY\).
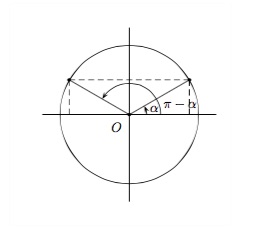
\(\begin{array}{ll} \displaystyle \sin (\pi -\alpha) = \sin \alpha\hspace{2cm}&tg\,(\pi -\alpha) = - tg\, \alpha\\ \displaystyle \cos (\pi -\alpha) = - \cos \alpha&cotg\,(\pi -\alpha) = - cotg\, \alpha \end{array}\)
Pour des angles anti-supplémentaires \(\alpha\) et \(\pi+\alpha\)
Dans un cercle trigonométrique, deux angles anti-supplémentaires sont représentés par deux points du cercle symétriques par rapport à l'origine \(O\).
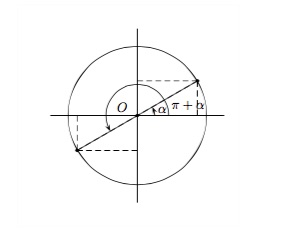
\(\begin{array}{ll} \displaystyle \sin (\pi +\alpha) = - \sin \alpha\hspace{2cm}&tg\,(\pi +\alpha) = tg\,\alpha\\ \displaystyle \cos (\pi +\alpha) = - \cos \alpha&cotg\,(\pi +\alpha) = cotg\,\alpha \end{array}\)
(c) Formules trigonométriques
Les formules suivantes relient les différents nombres trigonométriques.
Formule fondamentale
\(\sin^2 \alpha + \cos ^2 \alpha = 1\)
Formules de duplication
\(\sin (2\alpha) = 2 \sin \alpha \cos \alpha\)
\(\cos (2\alpha) = \cos ^2 \alpha - \sin ^2 \alpha = 1 - 2 \sin ^2 \alpha = 2 \cos ^2 \alpha - 1\)
\(\displaystyle tg\,{(2\alpha)} = \frac{2\, tg\,{\alpha}} {1- tg^2{\alpha}}\)
Formules d'addition
\(\begin{array}{ll} \sin (\alpha + \beta) = \sin \alpha \cos\beta + \sin \beta \cos \alpha &\hspace{1.5cm}\sin (\alpha -\beta) = \sin \alpha \cos\beta - \sin \beta \cos\alpha\\ \cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \beta \sin\alpha &\hspace{1.5cm}\cos (\alpha - \beta) = \cos \alpha \cos\beta + \sin \beta \sin \alpha\\ \displaystyle tg\, (\alpha + \beta) = \frac{tg\, \alpha+ tg\, \beta}{1- tg\,\alpha \cdot tg\, \beta} &\hspace{1.5cm}\displaystyle tg\, (\alpha - \beta) = {tg\,\alpha - tg\, \beta \over 1+ tg\, \alpha \cdot tg\, \beta} \end{array}\)
Formules de Carnot
\(\begin{array}{ll} \displaystyle \sin ^ 2 \alpha = {1 - \cos (2\alpha) \over 2}&\hspace{1.5cm} \displaystyle 1+tg^2 \alpha = {1\over \cos^2 \alpha}\\ \displaystyle \cos ^ 2 \alpha = {1 + \cos (2\alpha) \over 2}&\hspace{1.5cm} \displaystyle 1+cotg^2 \alpha = {1\over \sin^2 \alpha} \end{array}\)
Formules de Simpson
\(\begin{array}{l} \sin \alpha + \sin \beta = 2 \sin {(\frac{\alpha +\beta} {2})} \cos {(\frac{\alpha -\beta}{2})}\\[1mm] \sin \alpha - \sin \beta = 2 \sin {(\frac{\alpha -\beta}{2})} \cos {(\frac{\alpha +\beta} {2})}\\[1mm] \cos \alpha + \cos \beta = 2 \cos {(\frac{\alpha +\beta} {2})} \cos {(\frac{\alpha -\beta}{2})}\\[1mm] \cos \alpha - \cos \beta = -2 \sin {(\frac{\alpha -\beta}{2})} \sin {(\frac{\alpha +\beta}{2})} \end{array}\)
