Théorie du module : Géométrie et mesure
Table des matières
- Théorème de Thalès et proportions
- Cercles
- Polygones
- Triangles
- Quadrilatères
- Périmètre et aire de surfaces élémentaires
- Volume de solides élémentaires
- Mesures et grandeurs
- Exemples détaillés
Triangles
Un triangle est un polygone à trois côtés. Il a également trois sommets et trois angles. Un triangle qui a 3 côtés égaux est dit équilatéral. Un triangle isocèle a 2 côtés de même longueur et un triangle scalène est un triangle ayant ses 3 côtés de longueur différente.
(a) Triangles quelconques
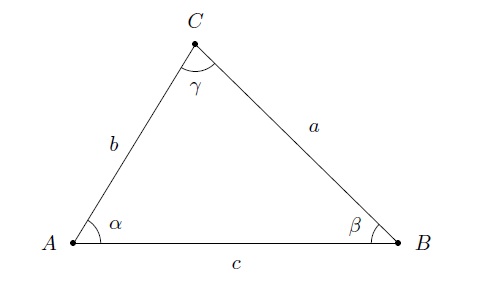
Un triangle quelconque est un triangle qui ne contient aucun angle droit. On utilise les lettres \(A,B,C\) pour les sommets du triangle, les lettres \(a,b,c\) pour les longueurs des côtés opposés à ces sommets, et \(\alpha, \beta, \gamma\) pour les angles en chacun des sommets.
On déduit du Théorème de Thalès et proportions le résultat suivant.
Réciproquement, dans tout triangle, le segment joignant les milieux de deux des côtés est parallèle au troisième côté et sa longueur vaut la moitié de celle de ce troisième côté.
La médiatrice d'un segment est la droite perpendiculaire au milieu de ce segment. Tous les points de cette droite sont à même distance des extrémités du segment. Réciproquement, tout point équidistant des extrémités d'un segment appartient à la médiatrice de ce segment.
Cliquez sur le lien pour la construction de la médiatrice d'un segment.
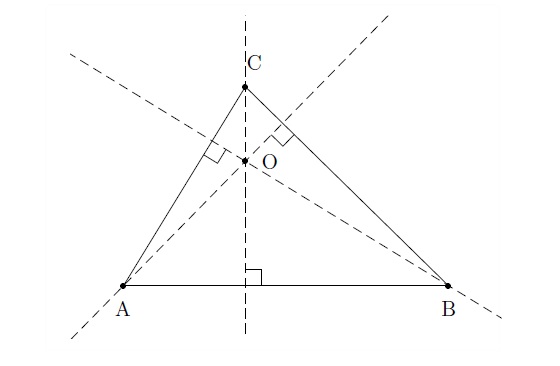
Une médiatrice d'un triangle est une droite perpendiculaire au milieu d'un de ses côtés. Un triangle a donc 3 médiatrices. On peut démontrer la propriété suivante.
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
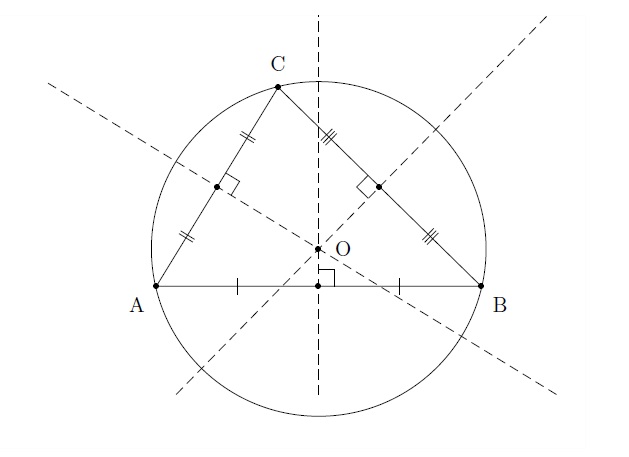
Le point d'intersection des trois médiatrices d'un triangle se trouve à égale distance des trois sommets du triangle. Ce point est donc le centre du cercle circonscrit au triangle. Par trois points non alignés, on peut donc faire passer un et un seul cercle.
La bissectrice d'un angle est la droite qui coupe cet angle en deux angles de même amplitude. Tous les points de cette droite sont à même distance des côtés de l'angle. Réciproquement, tout point équidistant des côtés d'un angle appartient à la bissectrice de cet angle.
Cliquez sur le lien pour la construction de la bissectrice d'un angle.
Une bissectrice d'un triangle est une droite qui coupe un de ses angles en deux angles de même amplitude. Un triangle a donc 3 bissectrices. On peut démontrer la propriété suivante.
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
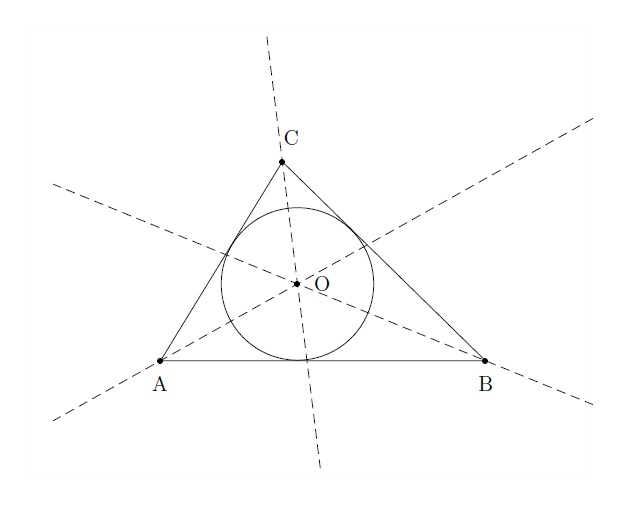
Le point d'intersection des trois bissectrices d'un triangle se trouve à égale distance des trois côtés du triangle. Ce point est donc le centre du cercle inscrit au triangle. Ce cercle est tangent à chaque côté du triangle.
Une médiane d'un triangle est une droite qui relie un des sommets au milieu du côté opposé. Un triangle a donc 3 médianes. On peut démontrer la propriété suivante.
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
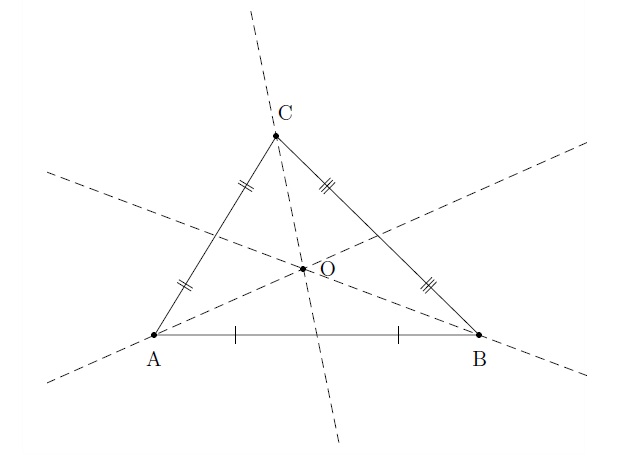
Le point d'intersection des trois médianes est le centre de gravité du triangle. Il est situé sur chaque médiane aux \(2/3\) de chacune d'elle à partir du sommet.
Une hauteur d'un triangle est une droite passant par un sommet et perpendiculaire au côté opposé (ou à son prolongement). Un triangle a donc 3 hauteurs. On peut démontrer la propriété suivante.
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
Le point d'intersection des trois hauteurs est l'orthocentre du triangle.
(b) Triangles isocèles
Un triangle isocèle est un triangle qui a deux côtés de même longueur. Le troisième côté est appelé base du triangle. On peut montrer les propriétés suivantes.
- les angles à la base ont même amplitude;
- la médiatrice de la base est égale à la bissectrice de l'angle opposé;
- la médiatrice de la base est aussi médiane;
- la médiatrice de la base est aussi hauteur.
(c) Triangles rectangles
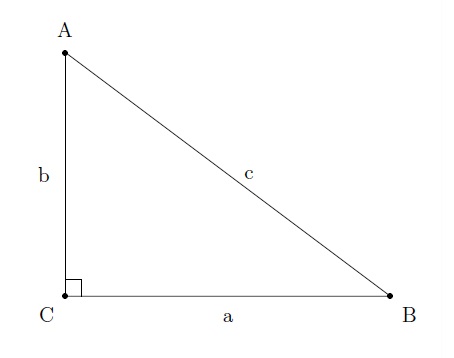
Un triangle rectangle est un triangle ayant un angle droit. Le côté opposé à l'angle droit est appelé hypoténuse du triangle rectangle. Le théorème principal dans les triangles rectangles est le Théorème de Pythagore.
\(a^2+b^2=c^2.\)
Si vous êtes intéressé, vous pouvez regarder la preuve de cette affirmation.
Les triangles rectangles possèdent les propriétés suivantes.
- Tout triangle inscrit dans un demi-cercle est rectangle.
- On peut inscrire tout triangle rectangle dans un demi-cercle dont le diamètre est l'hypoténuse du triangle.
- Dans un triangle rectangle, la longueur de la médiane relative à l'hypoténuse vaut la moitié de la longueur de l'hypoténuse.
- Dans un triangle rectangle, la carré de la longueur de la hauteur relative à l'hypoténuse est égal au produit des longueurs des segments qu'elle détermine sur l'hypoténuse.
(d) Triangles semblables
Deux triangles sont semblables s'ils leurs angles ont deux à deux la même amplitude.
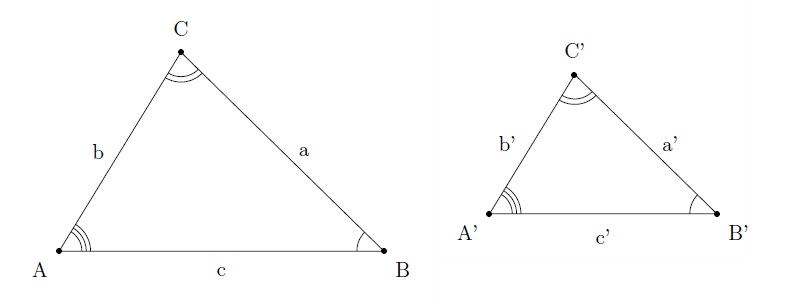
\(\displaystyle\frac{a}{a'}=\frac{b}{b'}=\frac{c}{c'}.\)
Remarque : Ces égalités impliquent par exemple que \(\frac{a}{c}=\frac{a'}{c'}\)ces valeurs sont donc égales pour tous les triangles semblables.
Les critères suivants permettent de voir si deux triangles sont semblables :
- Deux triangles sont semblables s'ils ont un angle de même amplitude dont les côtés correspondants sont proportionnels.
- Deux triangles sont semblables s'ils ont deux angles correspondants de même amplitude.
- Deux triangles sont semblables si leurs côtés correspondants sont proportionnels.
Par exemple, supposons qu'une personne de 1,80 m souhaite déterminer la hauteur d'un pont au dessus d'une rivière. Commençons par représenter la situation
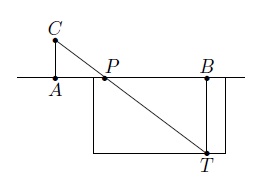
La personne se tient en \(A\) à un bout du pont et regarde le point \(T\) de la rivière en dessous de \(B\). Il note \(P\) l'endroit où sa vision rencontre le pont. Ce point \(P\) permet de former deux triangles : les triangles \(APC\) et \(BPT\). Ces deux triangles sont semblables car ils ont deux angles égaux : un angle droit (respectivement en \(A\) et en \(B\)) et les deux angles en \(P\). On peut maintenant calculer la hauteur du pont en utilisant les relations dans les triangles semblables : si \(|AP| \) vaut 3 m et si \(|PB| \) vaut 12 m, alors
\(\dfrac{|AC|}{|BT|}=\dfrac{|AP|}{|PB|} = \dfrac{3}{12}.\)
Donc \(|BT|= |AC|. \frac{12}{3}= (1,8). 4 = 7,2\) m.
