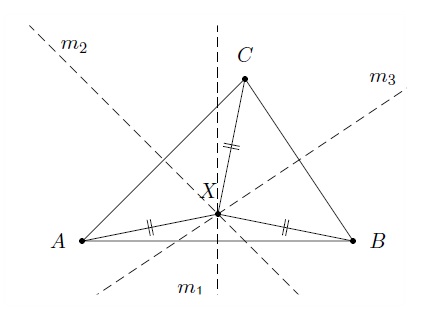
On considère le triangle quelconque \(ABC\) et soit \(m_1\) médiatrice du côté \(AB\), \(m_2\) médiatrice du côté \(AC\) et \(m_3\) médiatrice du côté \(BC\). Soit \(X\) le point d'intersection de \(m_1\) et \(m_2\). Voyons que \(m_1\), \(m_2\) et \(m_3\) se coupent au point \(X\).
Puisque \(X\in m_1\), on a que les segments \(XA\) et \(XB\) sont de même longueur. De même, puisque \(X\in m_2\), on a que les segments \(XA\) et \(XC\) sont de même longueur. On en déduit que les segments \(XB\) et \(XC\) sont de même longueur et donc que \(X\) est un point de la médiatrice \(m_3\).

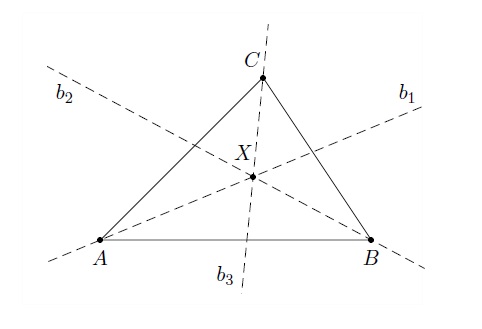
On considère le triangle quelconque \(ABC\) et soit \(b_1\) bissectrice de l'angle \(BAC\), \(b_2\) bissectrice de l'angle \(ABC\) et \(b_3\) bissectrice de l'angle \(BCA\). Soit \(X\) le point d'intersection de \(b_1\) et \(b_2\). Voyons que \(b_1\), \(b_2\) et \(b_3\) se coupent au point \(X\).
Tous les points de la droite \(b_1\) sont à même distance des côtés \(AB\) et \(AC\) et tous les points de la droite \(b_2\) sont à même distance des côtés \(BA\) et \(BC\). Puisque \(X\in b_1\) et \(X\in b_2\), on a que \(X\) est à même distance des côtés \(AC\) et \(BC\). On en déduit que \(X\) est un point de la bissectrice \(b_3\).

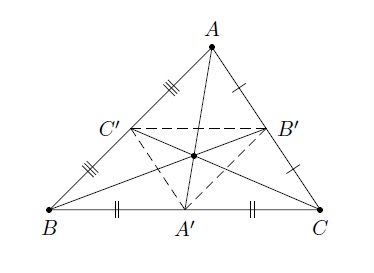
On considère le triangle quelconque \(ABC\) et soit \(A'\) le milieu du segment \(BC\), \(B'\) le milieu du segment \(AC\) et \(C'\) le milieu du segment \(AB\).

On déduit de la Proposition que \(C'B'\parallel BC\) et que la longueur du segment \(BC\) est le double de celle du segment \(B'C'\).

De même, la longueur du segment \(AB\) est le double de celle du segment \(A'B'\) et la longueur du segment \(AC\) est le double de celle du segment \(A'C'\).

Les triangles \(ABC\) et \(A'B'C'\) sont donc semblables et le triangle \(A'B'C'\) est l'image du triangle \(ABC\) par une homothétie. Les droites \(AA'\), \(BB'\) et \(CC'\) sont donc concourantes.

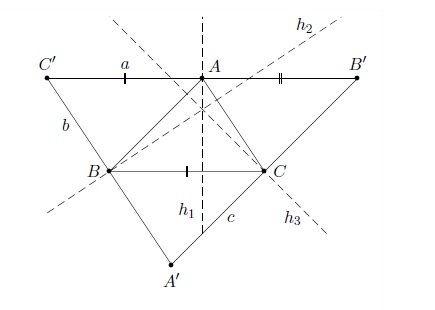
On considère le triangle quelconque \(ABC\) et soit \(h_1\) hauteur passant par \(A\), \(h_2\) hauteur passant par \(B\) et \(h_3\) hauteur passant par \(C\).
Traçons la droite \(a\) passant par \(A\) et parallèle au côté \(BC\), la droite \(b\) passant par \(B\) et parallèle au côté \(AC\) et la droite \(c\) passant par \(C\) et parallèle au côté \(AB\). Soit \(A'\) le point d'intersection de \(b\) et \(c\), \(B'\) le point d'intersection de \(a\) et \(c\) et \(C'\) le point d'intersection de \(a\) et \(b\).

Puisque \(b\parallel AC\) et \(a\parallel BC\) on en déduit que \(ACBC'\) est un parallélogramme et donc les segments \(C'A\) et \(BC\) ont même longueur. De même, puisque \(c\parallel AB\) et \(a\parallel BC\), on en déduit que \(AB'CB\) est un parallélogramme et donc les segments \(AB'\) et \(BC\) ont même longueur. Cela implique que les segments \(C'A\) et \(AB'\) ont même longueur et donc \(A\) est au milieu du segment \(B'C'\).
De plus, \(h_1\perp BC\) et \(BC\parallel B'C'\) donc \(h_1\perp B'C'\).
On en déduit que \(h_1\) est la médiatrice du segment \(B'C'\).

De la même façon, on montre que \(h_2\) est la médiatrice du segment \(A'C'\) et \(h_3\) est la médiatrice du segment \(A'B'\).
Puisque les trois médiatrices du triangle \(A'B'C'\) se coupent en un même point, on en déduit que \(h_1\), \(h_2\) et \(h_3\) se coupent en un même point.

Construisons un carré de côté \(a+b\) et décomposons-le de deux manières différentes :

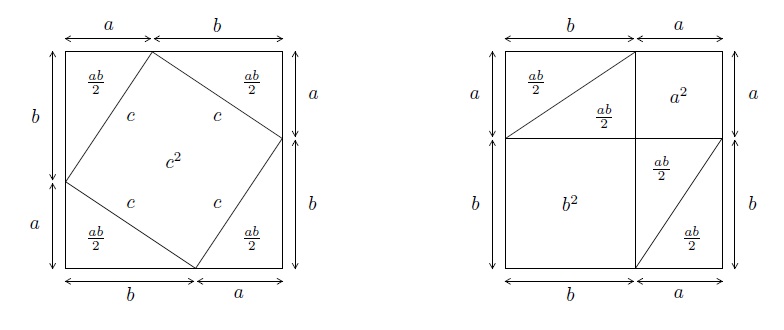
L'aire du premier carré est égale à

\(c^2+4\dfrac{ab}{2}=c^2+2ab.\)

Celle du deuxième carré est égale à

\(a^2+b^ 2+4\dfrac{ab}{2}=a^2+b^ 2+2ab.\)

Puisque les deux aires sont égales, on obtient \(a^2+b^2=c^2\).

Construction de la médiatrice d'un segment

Soit \(A\) et \(B\) deux points du plan. Pour construire la médiatrice du segment joignant \(A\) à \(B\) :

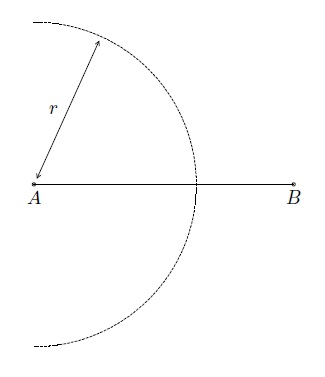
• choisir un nombre réel \(r>0\) supérieur à la moitié de la distance entre \(A\) et \(B\);
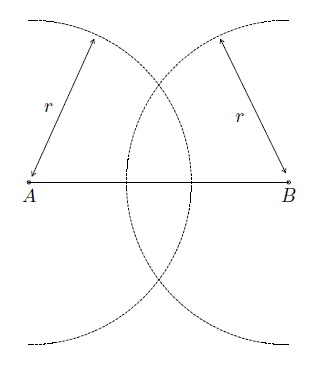
• tracer un arc de cercle de centre \(A\) et de rayon \(r\);
• tracer un arc de cercle de centre \(B\) et de rayon \(r\);
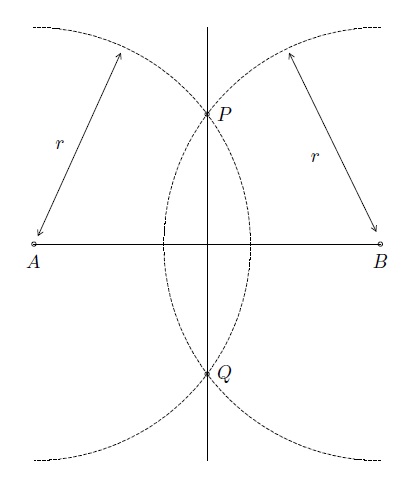
• ces deux arcs de cercle se coupent aux points \(P\) et \(Q\);
• la droite \(PQ\) est la médiatrice du segment reliant \(A\) et \(B\).

Construction de la bissectrice d'un angle

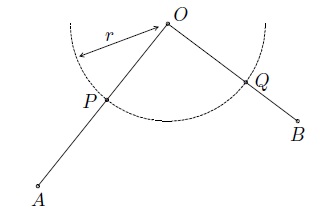
Soit \(O\), \(A\) et \(B\) trois points du plan. Pour construire la bissectrice de l'angle \(\widehat{AOB}\) :

• choisir un nombre réel \(r>0\);
• tracer un arc de cercle de centre \(O\) et de rayon \(r\);
• cet arc coupe les côtés de l'angle aux points \(P\) et \(Q\);
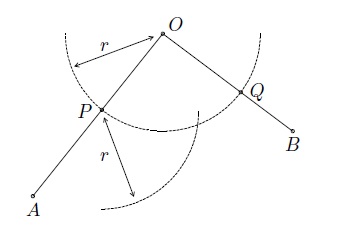
• tracer un arc de cercle de centre \(P\) et de rayon \(r\);
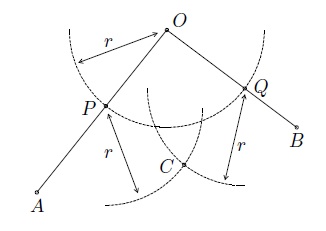
• tracer un arc de cercle de centre \(Q\) et de rayon \(r\);
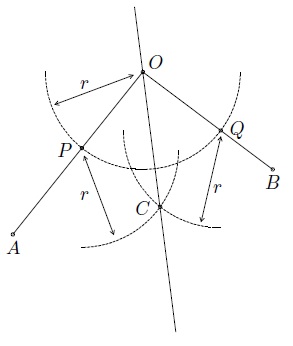
• ces deux arcs se coupent au point \(C\);
• la droite \(OC\) est la bissectrice de l'angle \(\widehat{AOB}\).