Théorie du module : Polynômes
Table des matières
Afficher toute la théorie du moduleExemples détaillés
- Donner le degré du polynôme \(P(x)=2x^2+4x+2\), l'évaluer en \(x=3\) et trouver les racines de ce polynôme.
Solution détaillée : Le polynôme \(P\) est de degré 2 et on a
\(P(3)=2\cdot 3^2+4\cdot 3+2=18+12+2=32\).
Pour trouver les racines de \(P\), on va le factoriser. On a \(P(x)=2(x^2+2x+1)=2(x+1)^2\), ce polynôme s'annule donc en \(x=-1\). On a \(P(-1)=0\) et \(x=-1\) est la seule racine de \(P\).
Solution détaillée : On obtient
\(\begin{array}{rcl} P(x)+Q(x) &= &3x^3-2x+1+x^4-2x^3-x^2+4x-2 \\ &= & x^4+x^3-x^2+2x-1 \end{array} \)
et
\(\begin{array}{rcl} P(x)\cdot Q(x) &= &(3x^3-2x+1)(x^4-2x^3-x^2+4x-2) \\ &= &3x^7-6x^6-3x^5+12x^4-6x^3-2x^5+4x^4+2x^3-8x^2\\ &&\hspace{6cm}+4x+x^4-2x^3-x^2+4x-2\\ &=&3x^7-6x^6-5x^5+17x^4-6x^3-9x^2+8x-2 \end{array} \)
- Effectuer la division de \(P(x)=x^5+x^4-3x^3+3x-2\) par \(D(x)=x^3-x+1\).
Solution détaillée : On fait le tableau suivant :
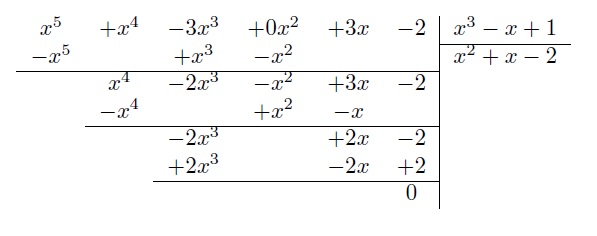
On obtient \(Q(x)=x^2+x-2\) et \(R(x)=0\), la division est donc exacte. On peut écrire
\(\dfrac{x^5+x^4-3x^3+3x-2}{x^3-x+1}=x^2 +x-2\)
ou encore
\(x^5+x^4-3x^3+3x-2=(x^3-x+1)(x^2 +x-2).\)
- Effectuer la division de \(P(x)=2x^4 -18x^2 + 2x +5\) par \(D(x)=x + 3\).
Solution détaillée : On fait le tableau suivant :
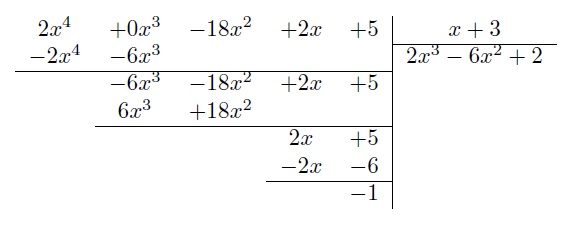
On obtient \(Q(x)=2x^3 -6x^2 + 2\) et \(R(x)=-1\). On peut écrire
\(\dfrac{2x^4 -18x^2 + 2x +5}{x + 3 } = 2x^3 -6x^2 + 2 - \dfrac{1}{x+3}\)
ou encore
\(2x^4 -18x^2 + 2x +5=(x + 3)(2x^3 -6x^2 + 2)-1.\)
Vu que le diviseur est un polynôme du premier degré, on peut également utiliser la règle de Horner pour effectuer cette division. On obtient
\(\begin{array}{c|cccc|c} &2&0&-18&2&5 \\ \hline -3&&-6&18&0&-6 \\ \hline &2&-6&0&2&-1 \end{array}\)
Le degré du quotient est \(4-1=3\) et ses coefficients se trouvent dans la dernière ligne du tableau. On trouve bien comme ci-dessus : \(Q(x)=2x^3 -6x^2 + 2\) et \(R(x)=-1\).
- Utiliser la règle de Horner pour diviser \(3x^3 - 6x^2 + 5x - 3\) par \(2x - 4\).
Solution détaillée : On ne peut pas utiliser directement la règle de Horner puisque le polynôme diviseur \(2x - 4\) n'est pas de la forme \(x - a\).
On remarque cependant que :
\(\dfrac{3x^3 - 6x^2 + 5x -3}{2x -4} =\dfrac{3x^3 - 6x^2 + 5x -3}{2(x -2)} =\dfrac{1}{2} \cdot \dfrac{3x^3 - 6x^2 + 5x -3}{x -2}. \)
On peut donc maintenant utiliser la règle de Horner pour diviser \(3x^3 - 6x^2 + 5x -3 \) par \(x - 2\).
\(\begin{array}{c|ccc|c} &3&-6&5&-3 \\ \hline 2&&6&0&10 \\ \hline &3&0&5&7 \end{array}\)
On obtient
\(\dfrac{3x^3 - 6x^2 + 5x -3}{x -2}=3 x^2 + 5 + \dfrac{7}{x-2}\)
et donc
\(\begin{array}{rcl} \dfrac{3x^3 - 6x^2 + 5x -3}{2x -4}& =&\dfrac{1}{2}\cdot\dfrac{3x^3 - 6x^2 + 5x -3}{x -2}\\ &&\\ &=&\dfrac{1}{2}\left( 3 x^2 + 5 + \dfrac{7}{x-2}\right) \\ &&\\ &=&\dfrac{3 x^2 + 5}{2}+\dfrac{7}{2x-4}. \end{array}\)
- Factoriser l'expression \(x^5-8x^3+16x\).
Solution détaillée : On commence par mettre \(x\) en évidence : \(x(x^4-8x^2+16)\).
On utilise alors le produit remarquable \((a-b)^2\) pour factoriser la parenthèse :
\(((x^2)^2-2\cdot 4(x^2)+4^2)=(x^2-4)^2.\)
Cette dernière parenthèse est du type \((a^2-b^2)\). On a donc \(x^2-4=(x-2)(x+2)\).
On obtient finalement
\(x^5-8x^3+16x=x(x^2-4)^2=x[(x-2)(x+2)]^2=x(x-2)^2(x+2)^2\).
- Factoriser l'expression \((x-y)^3-y^3\).
Solution détaillée : En utilisant le produit remarquable \((a^3-b^3)\), on obtient
\((x-y)^3-y^3=((x-y)-y)((x-y)^2+(x-y)y+y^2).\)
On effectue ensuite le produit remarquable dans la parenthèse : \((x-y)^2=x^2-2xy+y^2\),
ainsi que la distributivité : \((x-y)y=xy-y^2\).
On obtient finalement
\(\begin{array}{rcl} (x-y)^3-y^3& =&(x-2y)(x^2-2xy+y^2+xy-y^2+y^2)\\ &=&(x-2y)(x^2-xy+y^2). \end{array}\)
- Factoriser l'expression \(x^7-3x^5+3x^3-x\).
Solution détaillée : En groupant les premier et quatrième termes, ainsi que les deux termes du milieu, on obtient
\((x^7-x)-(3x^5-3x^3)=x(x^6-1)-3x^3(x^2-1).\)
Pour pouvoir mettre \(x(x^2-1)\) en évidence, il faut faire apparaître \((x^2-1)\) dans le premier terme. Ce premier terme est du type \((a^3-b^3)\). On a donc
\((x^6-1)=((x^2)^3-1^3)=(x^2-1)((x^2)^2+x^2\cdot 1+1^2)=(x^2-1)(x^4+x^2+1).\)
On obtient alors
\(\begin{array}{rcl} x^7-3x^5+3x^3-x& =&x(x^6-1)-3x^3(x^2-1)\\ &=&x(x^2-1)(x^4+x^2+1)-3x^3(x^2-1)\\ &=&x(x^2-1)(x^4+x^2+1-3x^2)\\ &=&x(x^2-1)(x^4-2x^2+1). \end{array}\)
Le facteur \(x^4-2x^2+1\) est un produit remarquable du type \((a-b)^2\). On obtient
\(\begin{array}{rcl} x^7-3x^5+3x^3-x& =&x(x^2-1)(x^4-2x^2+1)\\ &=&x(x^2-1)((x^2)^2-2\cdot x^2\cdot 1+1^2)\\ &=&x(x^2-1)(x^2-1)^2\\ &=&x(x^2-1)^3. \end{array}\)
La dernière parenthèse est du type \((a^2-b^2)\) : \(x^2-1=(x-1)(x+1)\).
Finalement, on a
\(x^7-3x^5+3x^3-x=x[(x-1)(x+1)]^3=x(x-1)^3(x+1)^3.\)
- Factoriser l'expression \(x^8+9\).
Solution détaillée : En ajoutant et retirant la quantité \(6x^4\), on fait apparaître un produit remarquable du type \((a+b)^2\) :
\(\begin{array}{rcl} x^8+9& =&x^8+9+6x^4-6x^4\\ &=&((x^4)^2+2\cdot 3\cdot x^4+3^2)-6x^4\\ &=&(x^4+3)^2-6x^4. \end{array}\)
On a alors un produit remarquable du type \(a^2-b^2\) :
\(\begin{array}{rcl} (x^4+3)^2-6x^4& =&(x^4+3)^2-(\sqrt{6}x^2)^2\\ &=&(x^4+3-\sqrt{6}x^2)(x^4+3+\sqrt{6}x^2)\\ &=&(x^4-\sqrt{6}x^2+3)(x^4+\sqrt{6}x^2+3). \end{array}\)
