Théorie du module : Polynômes
Table des matières
Afficher toute la théorie du moduleOpérations sur les polynômes
(a) Somme de polynômes
La somme de deux polynômes est le polynôme obtenu en additionnant entre eux les termes de même puissance.
Par exemple, \((3x^2-5x+6) + (x^3-x+2) = x^3+3x^2-6x+8\).
(b) Produit de polynômes
Le produit de deux polynômes est le polynôme obtenu en multipliant chaque terme de l'un par chaque terme de l'autre.
Par exemple, \((-x^3+2x^2+1)(3x-2)=-3x^4+6x^3+3x+2x^3-4x^2-2=-3x^4+8x^3-4x^2+3x-2\).
Remarque : Vous trouverez les règles de calcul des puissances en cliquant ici.
(c) Division de polynômes
La division d'un polynôme \(P(x)\) (dividende) par un polynôme \(D(x)\) (diviseur) donne un polynôme \(Q(x)\) (quotient) et un polynôme \(R(x)\) (reste) liés par les relations :
\(P(x) = D(x)\cdot Q(x) + R(x)\)
\(\mbox{où }\text{degré de }R(x) < \ \text{degré de } D(x)\)
\(\mbox{et }\text{degré de }Q(x) = \ \text{degré de } P(x) - \text{degré de } D(x)\)
Division euclidienne
Pour faire une division euclidienne, on réalise un tableau comme pour une division de nombres réels :
\(\begin{array}{c|c} P(x)&\underline{D(x)} \\ \underline{\ \ \ \ \vdots \ \ \ \ } & {Q(x)} \\ {R(x)} & \\ \end{array}\)
Cette division s'arrête lorsque le degré de \(R\) est strictement inférieur au degré de \(D\).
Par exemple, divisons le polynôme \(6x^4 - 2x^3 + 9x^2 - 2x - 2\) par le polynôme \(x^2 + 2\).
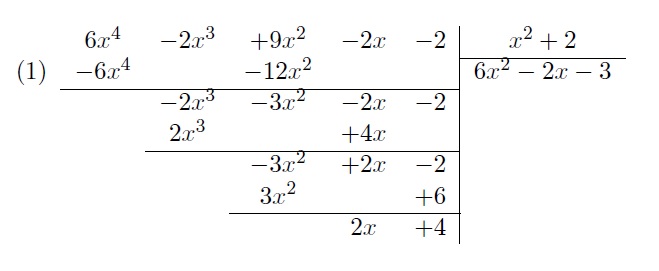
Le premier terme du quotient (\(6x^2\)) est obtenu en divisant le premier terme du dividende (\(6x^4\)) par le premier terme du diviseur (\(x^2\)).
On obtient alors la première ligne (1) en multipliant le diviseur (\(x^2 + 2\)) par le premier terme du quotient (\(6x^2\)). On poursuit ensuite en appliquant les règles usuelles de la division.
Le dernier terme (\(2x + 4\)), étant de degré inférieur à celui du diviseur, représente le reste de la division.
On a donc :
\(\dfrac{6x^4 - 2x^3 + 9x^2 - 2x - 2}{x^2 + 2} = 6x^2 - 2x - 3 + \dfrac{2x + 4}{x^2 + 2},\)
ou encore
\(6x^4 - 2x^3 + 9x^2 - 2x - 2=(x^2 + 2)(6x^2 - 2x - 3)+(2x + 4).\)
Loi du reste
Si le diviseur \(D(x)\) est un polynôme du premier degré de la forme \((x-a)\) , on a
\(P(x)=(x-a)\cdot Q(x)+R(x)\)
où le degré de \(R\) est strictement inférieur au degré de \((x-a)\). Donc \(R(x)\) est une constante et on peut écrire
\(P(x)=(x-a)\cdot Q(x)+R.\)
En prenant \(x=a\), on obtient :
\(P(a)=(a-a)\cdot Q(a)+R=R.\)
On a donc le résultat suivant :
On peut donc déterminer le reste d'une division d'un polynôme en \(x\) par \((x-a)\) sans déterminer le quotient et par là même vérifier si la division est exacte, c'est-à-dire si \(R=0\).
Par exemple, déterminons le reste de la division de \(P(x)= x^3-2x^2+x-1\) par \(x-4\). Ici, \(a=4\) et on obtient \(R=P(4)=4^3-2\cdot 4^2+4-1=35\).
Division d'un polynôme par \((x-a)\) : Règle de Horner
La règle de Horner ne peut être utilisée que lorsque le diviseur est un polynôme du premier degré.
Par exemple, divisons \(2x^4 - 18x^2 +2x + 5\) par \(x + 3\).
\(\begin{array}{c|cccc|c} &2&0&-18&2&5 \\ -3&&-6&18&0&\hline -6 \\ \hline &2&-6&0&2&-1 \end{array}\)
On dispose dans la première ligne du tableau les coefficients des puissances successives de \(x\) du dividende à commencer par la puissance la plus élevée; ainsi, 2 est le coefficient de \(x^4\), 0 celui de \(x^3\), -18 celui de \(x^2\), 2 celui de \(x\) et 5 est le terme indépendant.
Dans la première colonne de la deuxième ligne, on met le nombre \(a\) du polynôme diviseur lorsqu'il est mis sous la forme (\(x -a\)) (ici \(a = -3\) puisque le polynôme diviseur est \(x+3 = x - (-3)\)).
La troisième ligne est alors construite de gauche à droite de la manière suivante :
- le premier élément est le coefficient de \(x^4\);
- le deuxième élément (\(-6\)) est la somme du coefficient de \(x^3\) (0) et du produit de \(-3\) par l'élément précédement trouvé de la troisième ligne (\(2\)); ainsi, \(-6 = 0 + (-3)\cdot 2\);
- le troisième élément (\(0\)) est la somme du coefficient de \(x^2\) (\(-18\)) et du produit de \(-3\) par l'élément précédement trouvé de la troisième ligne (\(-6\)); ainsi, \(0 = -18 + (-3)\cdot (-6)\);
- ainsi de suite jusqu'au dernier élément de la ligne; ainsi, \(-1 = 5 + (-3)\cdot 2\).
On peut maintenant interpréter ce tableau : les éléments de la troisième ligne représentent les coefficients des puissances successives de \(x\) du quotient à commencer par la puissance la plus élevée. Comme \(P\) est de degré \(4\) et \(D\) est de degré \(1\), le polynôme \(Q\) est de degré \(4-1=3\) et donc \(Q(x)=2\cdot x^3+(-6)x^2+0\cdot x+2\).
Le dernier élément de cette ligne est le reste de la division, ici \(-1\).
On obtient finalement :
\(\dfrac{2x^4 -18x^2 + 2x +5}{x + 3 } = 2x^3 -6x^2 + 2 - \dfrac{1}{x+3}\)
ou encore
\(2x^4 -18x^2 + 2x +5=(x + 3)(2x^3 -6x^2 + 2)-1.\)
Pour voir le lien entre la division euclidienne et la Règle de Horner, vous pouvez cliquer ici.
