Pour simplifier l'écriture, considérons un polynôme de degré 3, \(P(x)=a_3x^3+a_2x^2+a_1x+a_0\), et divisions-le par un polynôme du premier degré \((x-a)\). La division euclidienne s'effecue de la manière suivante

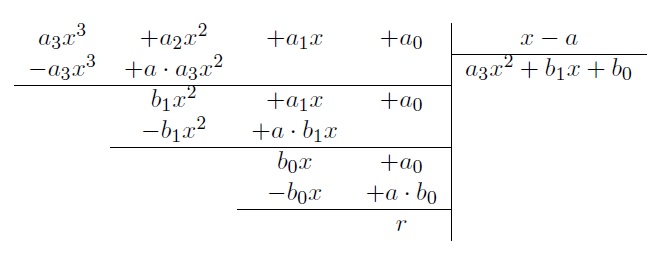
où \(b_1=a_2+a\cdot a_3\), \(b_0=a_1+a\cdot b_1\) et \(r=a_0+a\cdot b_0\).

On remarque que

• Le coefficient du premier terme du quotient (\(a_3\)) est le coefficient du premier terme du dividende (\(a_3\));
• Le coefficient du deuxième terme du quotient (\(b_1\)) s'obtient en ajoutant au coefficient du deuxième terme du dividende (\(a_2\)) le produit du coefficient du premier terme du quotient (\(a_3\)) par \(a\);
• Le coefficient du troisième terme du quotient (\(b_0\)) s'obtient en ajoutant au coefficient du troisième terme du dividende (\(a_1\)) le produit du coefficient du deuxième terme du quotient (\(b_1\)) par \(a\);
• Le reste (\(r\)) s'obtient en ajoutant au terme indépendant du dividende (\(a_0\)) le produit du terme indépendant du quotient (\(b_0\)) par \(a\).

Ceci peut également être écrit dans un tableau de Horner de la façon suivante

\(\begin{array}{c|ccc|c} &a_3&a_2&a_1&a_0 \\ \hline a&&+a.a_3&+a.b_1&+a.b_0 \\ \hline &a_3&b_1&b_0&r \end{array}\)

Ce résultat se généralise pour des polynômes de degré \(n\).

Soit \(P(x)=b_nx^n+b_{n-1}x^{n-1}+\cdots +b_1x+b_0\). On a

\(\begin{array}{rcl} P(a)=0 &\Leftrightarrow &b_na^n+b_{n-1}a^{n-1}+\cdots +b_1a+b_0=0 \\ &\Leftrightarrow & b_0=-(b_na^n+b_{n-1}a^{n-1}+\cdots +b_1a)\\ &\Leftrightarrow & b_0=-a(b_na^{n-1}+b_{n-1}a^{n-2}+\cdots +b_1) \end{array} \)

Donc \(a\) est racine de \(P\) si et seulement si \(a\) est un diviseur de \(b_0\). On peut alors écrire

\(\begin{array}{rcl} P \mbox{ est divisible par } x-a &\Leftrightarrow &P(a)=0 \\ &\Leftrightarrow & a \mbox{ est un diviseur du terme indépendant de } P \\ \end{array} \)