Théorie du module : Droites
Table des matières
Afficher toute la théorie du moduleEquations du premier degré - droites
Une équation du premier degré à deux inconnues \(ax+by+c=0\) est représentée dans le plan cartésien par une droite. Un point appartient à cette droite si et seulement si ses coordonnées vérifient l'équation de la droite.
Par exemple, considérons la droite \(D:y=2x-1\). On a \((2,3) \in D\) car \(3=2\cdot 2-1\) mais \((3,1) \not \in D\) puisque \(1\neq 2\cdot 3-1\).
En pratique, pour représenter une droite, il suffit de choisir deux points de cette droite et de les relier. Par facilité, on choisit souvent les intersections de la droite avec les deux axes de coordonnées.
(a) Equation vectorielle de la droite
Soient \(A\) et \(B\) deux points distincts du plan. Le point \(P\) appartient à la droite \(AB\)
- si et seulement si le vecteur \(\overrightarrow{AP}\) est un multiple du vecteur \(\overrightarrow{AB}\),
- si et seulement si il existe un réel \(k\neq 0\) tel que \(\overrightarrow{AP}=k\, \overrightarrow{AB}\).
Soient \(A=(x_{a},y_{a})\), \(B=(x_{b},y_{b})\) et \(P=(x,y)\). Comme \(\overrightarrow{AB}=(x_{b}-x_{a},y_{b}-y_{a})\) et \(\overrightarrow{AP}=(x-x_{a},y-y_{a})\), on a
\(\left\{ \begin{array}{c} x-x_{a}=k(x_{b}-x_{a}) \\ y-y_{a}=k(y_{b}-y_{a}) \end{array} \right.\)
Pour des rappels concernant les vecteurs, cliquez ici.
(b) Equation cartésienne de la droite
L'équation cartésienne d'une droite (non verticale) peut s'écrire :
(1.1)
\( y=mx+p\)
où
- \(p\) est l'ordonnée à l'origine, c'est-à-dire que \(p\) est l'ordonnée du point d'intersection de la droite avec l'axe \(OY\). Le point \((0,p)\) appartient donc à la droite.
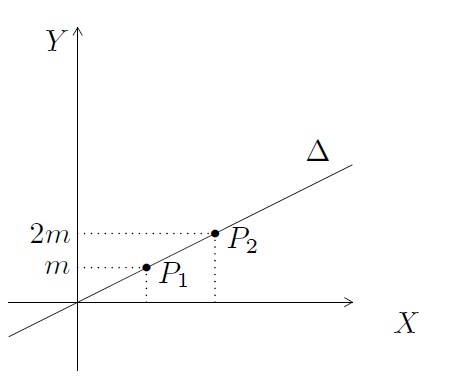
- \(m\) est la pente de la droite. Il s'agit de l'augmentation de l'ordonnée pour une augmentation unitaire des abscisses et ceci quel que soit l'endroit où l'augmentation de \(x\) est considérée. Par exemple, entre \(0\) et \(P_1\), l'augmentation des ordonnées est de \(m-0=m\), et entre \(P_1\) et \(P_2\), l'augmentation des ordonnées est de \(2m-m=m\).
Equation d'une droite passant par deux points donnés
Une droite est entièrement déterminée par deux points distincts du plan. Soit \(P_1=(x_1,y_1)\) et \(P_2=(x_2,y_2)\) deux points par lesquels passe la droite.
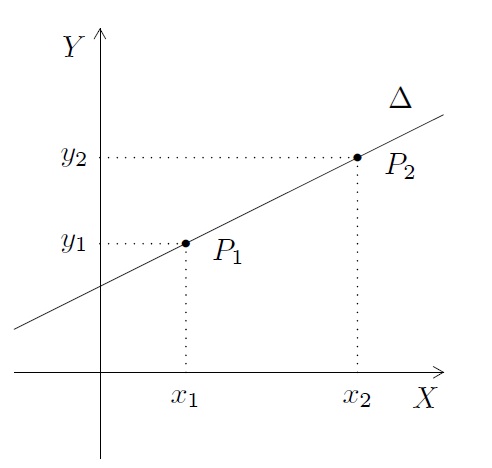
L'équation de la droite \(y= m x +p\) doit être satisfaite par les deux points \((x_1,y_1)\) et \((x_2,y_2)\). On a donc
\(\left\{\begin{array}{l} y_1 = m x_1 + p, \\ y_2 = m x_2 +p. \end{array}\right.\)
En soustrayant les deux équations, on élimine le paramètre (inconnu) \(p\). On obtient alors
\(y_2-y_1 = m (x_2-x_1),\)
ou encore
\( m = \dfrac{y_2-y_1}{x_2-x_1}.\)
En remplaçant \(m\) dans la première équation, on trouve
\(p=y_1-\dfrac{y_2-y_1}{x_2-x_1}x_1.\)
\(y-y_1 = \dfrac{y_2-y_1}{x_2-x_1} (x-x_1).\)
Par exemple la droite passant par les points \((-1,-5)\) et \((1,3)\) a pour équation \(y=4x-1\). En effet, on a
\(\begin{array}{c} y-(-5)=\frac{3-(-5)}{1-(-1)}(x-(-1)), \\ y+5=4(x+1), \\ y=4x+4-5, \\ y=4x-1. \end{array} \)
Cas particuliers :
- Si \(y_{1}=y_{2}\), la pente est nulle et la droite est parallèle à l'axe des \(x\) (droite horizontale). Dans ce cas, la droite a pour équation \( y=y_{1}\)
Ainsi, l'équation de l'axe des abscisses est donnée par : \(y=0.\)
- Si \(x_{1}=x_{2}\), la pente est infinie et la droite est parallèle à l'axe des \(y\) (droite verticale). Dans ce cas, la droite a pour équation \(x=x_{1}\). Cette équation n'est pas celle d'une fonction.
Ainsi, l'équation de l'axe des ordonnées est donnée par : \(x=0.\)
En pratique, pour représenter une droite dont on connaît deux points, il suffit de placer ces deux points dans un repère et de les relier.
Equation d'une droite de pente donnée et passant par un point donné
Si une droite est parfaitement définie par la donnée de deux de ses points, elle l'est aussi par la donnée d'un de ses points (par exemple le point d'intersection de cette droite avec l'axe des ordonnées) et de sa pente.
Soit \(m\) la pente de la droite et \(P_1=(x_1,y_1)\) un point par lequel passe cette droite.
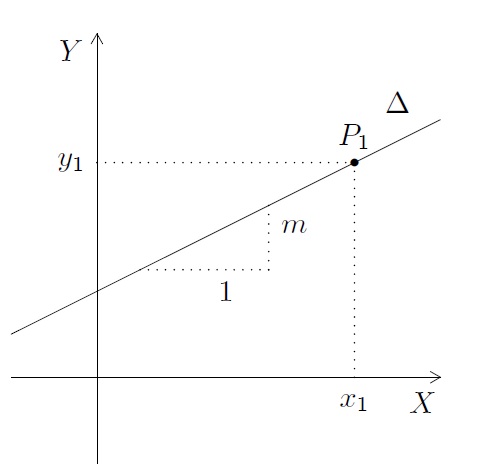
Vu que la pente est connue, il reste à déterminer le paramètre \(p\) dans l'équation \(y=mx+p\). Puisque \((x_1,y_1)\) vérifie l'équation de la droite, on a
\(y_1 = m x_1 + p,\)
d'où la valeur du paramètre \(p\) :
\(p = y_1 - m x_1.\)
L'équation devient alors \(y= mx+y_1-mx_1\).
\(y-y_1 = m (x-x_1).\)
Par exemple la droite de pente 4 et passant par le point \((1,3)\) a pour équation \(y=4x-1\). En effet, on a
\( \begin{array}{c} y-3=4(x-1), \\ y=4x-4+3, \\ y=4x-1. \end{array} \)
En pratique, pour représenter la droite \(y=m x+p\), on place le point \((0,p)\). Partant de ce point, on avance d'une unité vers la droite, puis on monte (si \(m> 0\)) ou on descend (si \(m< 0\)) d'une longueur \(m\). On obtient ainsi un deuxième point. Il ne reste plus qu'à joindre ces deux points.
Remarque :
- Considérons la droite \(y=mx+p\). On remarque que, pour \(p\) fixé, la pente de la droite varie avec \(m\). Par contre, si on fixe \(m\), on obtient en faisant varier \(p\) des droites parallèles entre elles. L'ajout du terme \(p\) a pour seul effet de déplacer la droite vers le haut (ou le bas) d'une distance égale à \(p\).
- Si \(m>0\) alors la droite est croissante, si \(m<0\) alors la droite est décroissante.
- Si, en déplaçant un point sur la droite, on augmente son abscisse de \(1\), alors son ordonnée augmente de \(m\) (positif ou négatif).
- Si, en déplaçant un point sur la droite, on augmente son abscisse de \(\Delta x\), alors son ordonnée augmente de \(\Delta y = m\cdot \Delta x\). Donc \(\displaystyle m = \frac{\Delta y}{\Delta x}\).
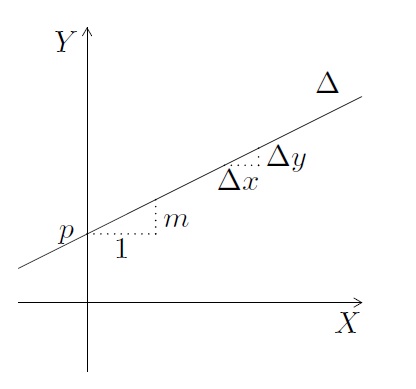
- Ayant choisi un système d'axes perpendiculaires avec des unités de même longueur (repère orthonormé), on a
\(m= \mbox{tg} \, \alpha,\)
où \(\alpha\) est l'angle entre l'axe des \(x\) positif et la droite, dans le sens trigonométrique.
Dans ce cas, la pente est aussi appelée coefficient angulaire de la droite.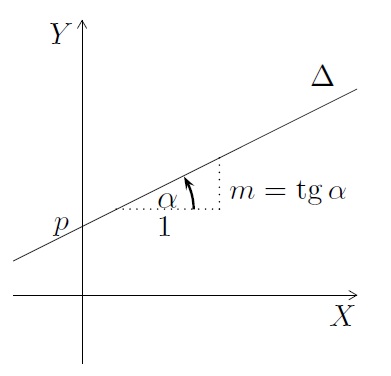
Forme générale de l'équation d'une droite
Plus généralement, l'équation d'une droite sera donnée par une relation linéaire du type
(1.2)
\( a x + b y = c.\)
Cette formulation est plus générale que la précédente car elle peut admettre \(b=0\), ce qui n'était pas le cas avec la formulation précédente.
- Si \(b=0\) et \(a\neq 0\), l'équation (1.2) se réduit à \(x = \frac{c}{a}\). Cette équation signifie que, quelle que soit la valeur de \(y\), \(x\) est une constante. Graphiquement, on a donc une droite verticale.
En particulier, l'équation de l'axe des ordonnées est donnée par \(x=0\).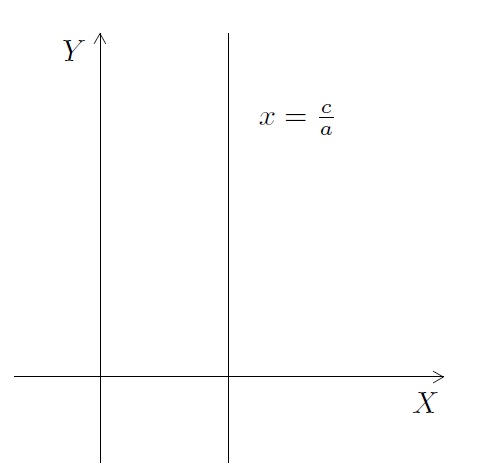
- Si \(b\not=0\) et \(a\neq 0\), on peut réécrire (1.2) comme
\(y = -\frac{a}{b} x + \frac{c}{b}.\)
On s'est donc ramené à l'équation du type (1.1) avec \(m = -\frac{a}{b}\) et \(p=\frac{c}{b}\). - Si \(b\not=0\) et \(a=0\), on a une équation du type \(y = \frac{c}{b}\) qui dit que quelle que soit la valeur de \(x\), la valeur de \(y\) est constante. Il s'agit d'une droite horizontale.
En particulier, l'équation de l'axe des abscisses est donnée par \(y=0\).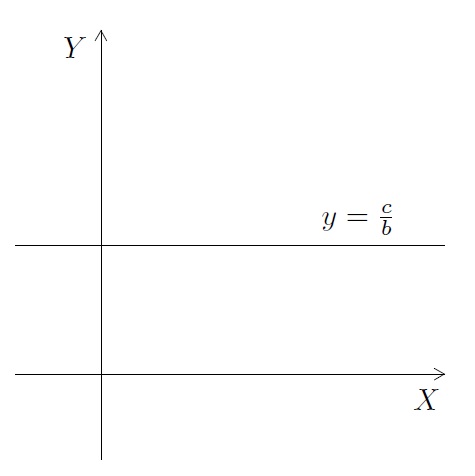
Position relative de deux droites
- Deux droites sont parallèles distinctes si et seulement si elles ont la même pente (\(m\)) et des ordonnées à l'origine (\(p\)) différentes.
Par exemple, les droites \(y=3x+2\) et \(y=3x-1\) sont parallèles.
- Deux droites sont sécantes si et seulement si elles ont des pentes différentes.
Par exemple, les droites \(y=3x+2\) et \(y=5x-1\) sont sécantes.
- Deux droites sont perpendiculaires si et seulement si le produit de leur pente vaut \(-1\) (ou si une des droites est verticale et l'autre horizontale).
Par exemple, les droites \(y=3x+1\) et \(y=-\frac{1}{3}x-1\) sont perpendiculaires.
Si vous êtes intéressé, vous pouvez regarder la preuve de cette dernière affirmation.
Les coordonnées du point d'intersection de deux droites sont obtenues en résolvant le système formé par leurs équations.
Pour plus de détails concernant les systèmes, cliquez ici.
Exemples détaillés
- Les points \((2,5)\), \((0,-4)\) et \((4,8)\) appartiennent-ils à la droite \(D: y=3x-4\) ?
Solution détaillée : On a
- \((2,5)\not\in D\). En effet, quand on remplace \(x\) par \(2\) et \(y\) par \(5\) dans l'équation de \(D\), celle-ci n'est pas vérifiée puisque \(5\neq 3\cdot 2-4\);
- \((0,-4)\in D\) car \(-4=3\cdot 0-4\);
- \((4,8)\in D\) car \(8=3\cdot 4-4\).
- Déterminer l'équation de la droite passant par les points \((1,2)\) et \((-3,6)\).
Solution détaillée : On obtient
\(y-2=\dfrac{6-2}{-3-1}(x-1)\)
c'est-à-dire \(y=-x+3\).
- Déterminer l'équation de la droite passant par les points \((-1,3)\) et \((7,3)\).
Solution détaillée : On a \(y_1=y_2=3\). Il s'agit donc d'une droite horizontale qui a pour équation \(y=3\).
- Déterminer l'équation de la droite passant par les points \((-1,3)\) et \((-1,-5)\).
Solution détaillée : On a \(x_1=x_2=-1\). Il s'agit donc d'une droite verticale qui a pour équation \(x=-1\).
- Les points \((0,-3)\), \((-2,7)\) et \((\frac{3}{2},0)\) appartiennent-ils à la même droite ?
Solution détaillée : Ces trois points n'appartiennent pas à la même droite. En effet, la droite \(D\) passant par \((0,-3)\) et \((-2,7)\) a pour équation
\(y-(-3)=\dfrac{7-(-3)}{-2-0}(x-0)\)
c'est-à-dire \(y=-5x+3\) et le point \((\frac{3}{2},0)\not\in D\).
- Ecrire l'équation cartésienne de la droite \(D\) définie par \(m=-2\) et \((1,0) \in D\).
Solution détaillée : Cette droite a pour équation \(y-0=-2(x-1)\) ou encore \(y=-2x+2\).
- Déterminer la pente de la droite \(3x-2y+4=0\).
Solution détaillée : En isolant \(y\) dans l'équation \(3x-2y+4=0\), on trouve \(y=\frac{3}{2}x+2\) et donc la pente (qui est le coefficient de \(x\) quand on a isolé \(y\)) vaut \(\frac{3}{2}\).
- Déterminer l'équation de la droite passant par \(P=(5,-7)\) qui est parallèle à la droite \(6x+3y=4\).
Solution détaillée : La pente de la droite donnée est \(-2\) car on peut écrire \(y=-2x+\frac{4}{3}\).
On recherche une droite d'équation\(y=-2x+ p \) passant par \(P=(5,-7)\).
- Première résolution : \(p \) vérifie \(-7=-2\cdot 5+p\); d'où \(p=3\). L'équation de la droite cherchée est \(y=-2x+ 3 \)
- Deuxième résolution : l'équation de la droite cherchée est \(y-y_1=-2(x-x_1) \), c'est-à-dire \(y-(-7)=-2(x-5) \) ou encore \(y=-2x+ 3 \).
- Déterminer l'équation de la droite passant par \(P=(5,-7)\) qui est perpendiculaire à la droite \(6x+3y=4\).
Solution détaillée : La pente de la droite \(6x+3y=4\) est \(-2\). La pente \(m\) de la droite cherchée vérifie l'égalité \(m .(-2)= -1\). Donc \(m \) vaut \(\frac{1}{2}\).
L'équation de la droite cherchée est : \(y-y_1=\frac{1}{2}(x-x_1) \), c'est-à-dire \(y-(-7)=\frac{1}{2}(x-5) \) ou encore \(y=\frac{1}{2}x-\frac{19}{2}\).
- Donner l'équation cartésienne de la droite \(D\) passant par le point \((2,-3)\) et qui est parallèle à \(D'\) qui passe par les points \((5,4)\) et \((6,2)\).
Solution détaillée : Cherchons d'abord l'équation de la droite \(D'\). Cette droite contient les points \((5,4)\) et \((6,2)\). Elle a donc pour équation \(y-4=\dfrac{2-4}{6-5}(x-5)\) ou encore \(y=-2x+14\).
La pente de \(D'\) vaut donc \(-2\) et comme \(D\) est parallèle à \(D'\), la pente de \(D\) vaut aussi \(-2\). On recherche alors une droite de pente \(-2\) passant par le point \((2,-3)\).
Cette droite a pour équation \(y-(-3)=-2(x-2) \) ou encore \(y=-2x+ 1\).
Preuves
Considérons les droites \(AB\) et \(AC\) où \(A=(x_a,y_a)\), \(B=(x_b,y_b)\) et \(C=(x_c,y_c)\), avec \(x_a\neq x_b\) et \(x_a\neq x_c\). On a
\(\begin{array}{rcl} AB\perp AC&\Longleftrightarrow&\overrightarrow{AB}\odot \overrightarrow{AC}=0\\ &\Longleftrightarrow&(x_b-x_a,y_b-y_a)\odot(x_c-x_a,y_c-y_a)=0\\ &\Longleftrightarrow&(x_b-x_a)(x_c-x_a)+(y_b-y_a)(y_c-y_a)=0\\ &\Longleftrightarrow&(y_b-y_a)(y_c-y_a)=-(x_b-x_a)(x_c-x_a)\\ & & \\ &\Longleftrightarrow&\dfrac{(y_b-y_a)}{(x_b-x_a)}\cdot\dfrac{(y_c-y_a)}{(x_c-x_a)}=-1\\ & & \\ &\Longleftrightarrow&m_1\cdot m_2=-1 \end{array} \)
où \(m_1\) est la pente de la droite \(AB\) et \(m_2\) est la pente de la droite \(AC\).
Remarque : Les deux premières équivalences sont des propriétés du produit scalaire.
Cliquez sur les liens pour des rappels sur les vecteurs et le produit scalaire.
