Théorie du module : Géométrie et mesure
Table des matières
- Théorème de Thalès et proportions
- Cercles
- Polygones
- Triangles
- Quadrilatères
- Périmètre et aire de surfaces élémentaires
- Volume de solides élémentaires
- Mesures et grandeurs
- Exemples détaillés
Volume de solides élémentaires
On appelle polyèdre un solide limité de toutes parts par des portions de plans.
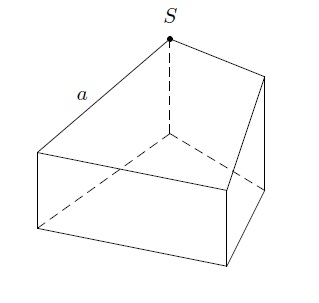
Les faces d'un polyèdre sont les polygones plans qui composent la surface du polyèdre. Les arêtes (a) d'un polyèdre sont les côtés des polygones qui forment les faces du polyèdre. Les sommets (S) du polyèdre sont les extrémités des arêtes. Le développement d'un polyèdre est la figure plane obtenue par la mise à plat de sa surface.
Un prisme est un polyèdre ayant pour base deux polygones égaux et parallèles et dont les faces latérales sont des parallélogrammes.
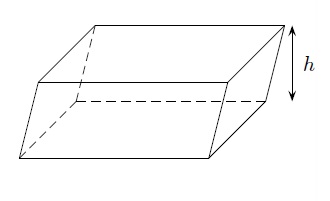
La hauteur d'un prisme est la distance entre les plans des bases. C'est la hauteur de la perpendiculaire commune aux deux bases. Un prisme est droit lorsque les arêtes latérales sont perpendiculaires à la base, sinon on dit qu'il est oblique.
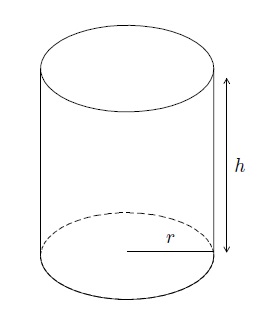
Un cylindre droit est un solide borné par une région plane \(B_1\), appelée la base et une région identique \(B_2\) dans un plan parallèle. Le cylindre est constitué de tous les points des segments perpendiculaires à la base qui relient \(B_1\) à \(B_2\).

En général, si \(B\) désigne l'aire de la base et \(h\) la hauteur d'un solide, alors le volume \(V\) du solide est défini par la formule
\(V=Bh.\)
Voici les formules permettant de calculer le volume de quelques solides simples.
(a) Parallélipipède rectangle
Le parallélipipède rectangle dont la base est un rectangle de longueur \(L\) et de largeur \(l\) et dont la hauteur est \(h\) a pour volume le nombre \(V=Llh\).

En particulier, le cube d'arête \(c\) a pour volume le nombre \(V=c^3\).
(b) Cylindre circulaire droit
Le cylindre circulaire droit dont la base est un disque de rayon \(r\) et dont la hauteur est \(h\) a pour volume le nombre \(V=\pi\, r^2\, h\).
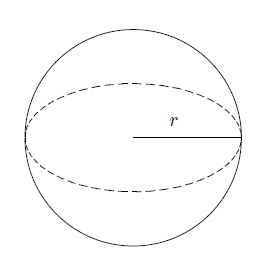
(c) Sphère
La sphère de rayon \(r\) a pour volume le nombre \(V=\dfrac{4\pi\, r^3}{3}\).