Théorie du module : Systèmes
Table des matières
- Système de deux équations à deux inconnues
- Système de plus de deux équations
- Système de m équations à n inconnues
- Exemples détaillés
Système de deux équations à deux inconnues
Toute équation du premier degré à deux inconnues possède une infinité de solutions. En effet, sa représentation graphique est une droite qui comporte une infinité de points dont les coordonnées sont des solutions de cette équation. Si l'on considère un système de deux équations à deux inconnues, ses solutions seront les couples de réels \((x,y)\) vérifiant à la fois la première et la seconde équation.
On veut donc résoudre le système
\( \left\{ \begin{array}{l} ax+by=c \\ a'x+b'y=c' \end{array} \right.\)
formé par les équations des deux droites \(D_1 : ax+by=c\) et \(D_2 : a'x+b'y=c'\).
(a) Interprétation géométrique
Si \(b\neq 0\) et \(b'\neq 0\), ce système peut encore s'écrire
(1.1)
\(\left\{ \begin{array}{l} y=mx+p \\ y=m'x+p' \end{array} \right. \)
Notons \(S\) l'ensemble des points de \(\mathbb{R}^2\) vérifiant le système. Autrement dit
\(S = \{ (x,y)\in\mathbb{R}^2:\, (x,y)\mbox{ satisfait la relation (1.1)}\}.\)
L'ensemble \(S\) comprend les points de l'intersection des 2 droites. Plusieurs cas sont possibles en fonction des paramètres des 2 droites.
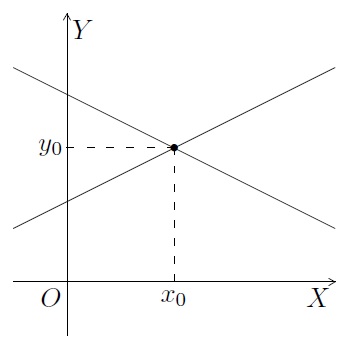
- Les deux droites sont sécantes - Si \(m\neq m'\), les deux droites sont sécantes et ont alors un seul point commun, le point \((x_0,y_0)\). Le système aura une solution unique notée \(S=\{(x_{0},y_{0})\}\).
- Les deux droites sont parallèles distinctes - Si \(m=m'\) et \(p \not = p'\), les deux droites sont parallèles et distinctes. Elles n'ont donc aucun point en commun. Le système n'aura aucune solution. On dit qu'il est impossible et on note \(S=\emptyset\).
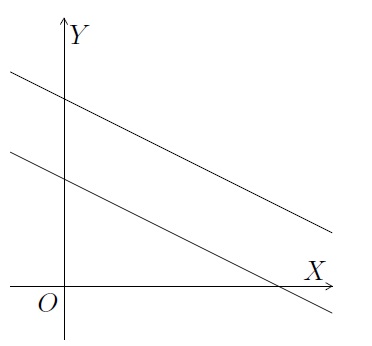
- Les deux droites sont parallèles confondues - Si \(m=m'\) et \(p=p'\), les deux droites sont confondues. Elles ont tous leurs points en commun. Le système a une infinité de solutions. On dit qu'il est indéterminé et on note \(S=\{(x,y)\,|\, y=mx+p\}\).
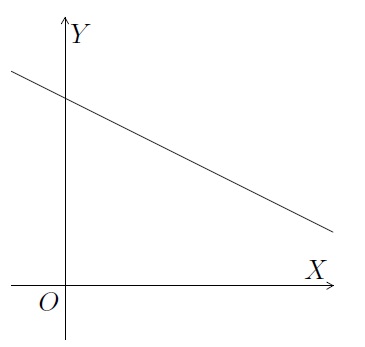
(b) Méthodes de résolution
Voyons à présent trois méthodes pour résoudre un système de deux équations à deux inconnues.
Cette méthode repose sur les deux principes suivants :
Premier principe - On peut multiplier n'importe quelle équation du système par une constante \(k \neq 0\) et on obtient un système équivalent.
Ce premier principe est clair au vu de l'interprétation géométrique. En effet, multiplier tous les coefficients d'une droite par une constante \(k \neq 0\) conduit à la même droite et donc ne modifie pas le système.
Second principe - On peut remplacer une équation du système par sa somme avec n'importe quelle équation du système et on obtient un système équivalent.
En effet, tout point \((x,y)\) vérifiant l'équation de la première droite et l'équation de la deuxième droite vérifie également l'équation obtenue en additionnant les deux équations et réciproquement.
- Aligner les inconnues et le terme indépendant.
- Multiplier les équations par un réel de telle manière qu'en faisant la somme des équations, une des inconnues disparaisse.
- Isoler l'inconnue restante.
- Remplacer cette inconnue par sa valeur dans l'équation restante.
Résolvons par exemple le système \(\left\{ \begin{array}{l} 3x+2y=9 \\ 4x=y+1 \end{array} \right.\)
On a successivement
| \(\left\{ \begin{array}{l} 3x+2y=9 \\ 4x=y+1 \end{array} \right.\) | \(\left\{ \begin{array}{l} 3x+2y=9 \\ 4x-y=1 \end{array} \right.\) | \(\left\{ \begin{array}{l} 12x+8y=36 \\ -12x+3y=-3 \end{array} \right.\) | \(\left\{ \begin{array}{l} 12x+8y=36 \\ 11y=33 \end{array} \right. \) |
| \( \left\{ \begin{array}{l} 12x+8y=36 \\ y=3 \end{array} \right. \) | \( \left\{ \begin{array}{l} 12x+24=36 \\ y=3 \end{array} \right.\) | \(\left\{ \begin{array}{l} 12x=12 \\ y=3 \end{array} \right. \) | \( \left\{ \begin{array}{l} x=1 \\ y=3 \end{array} \right. \) |
et donc \( S=\{(1,3)\}\).
- Isoler une des inconnues dans une des équations.
- Remplacer l'inconnue isolée (substituer) par sa valeur dans l'autre équation.
- Isoler l'inconnue restante.
- Remplacer cette inconnue par sa valeur dans l'équation restante.
Résolvons le même système que ci-dessus par cette méthode. On a successivement
| \(\left\{ \begin{array}{l} 3x+2y=9 \\ 4x=y+1 \end{array} \right. \) | \(\left\{ \begin{array}{l} x=3-\frac{2}{3} y \\ 4x-y=1 \end{array} \right. \) | \(\left\{ \begin{array}{l} x=3-\frac{2}{3} y \\ 4(3-\frac{2}{3} y)-y=1 \end{array} \right. \) | \(\left\{ \begin{array}{l} x=3-\frac{2}{3} y \\ -\frac{11}{3} y=-11 \end{array} \right. \) |
| \(\left\{ \begin{array}{l} x=3-\frac{2}{3} y \\ y=3 \end{array} \right. \) | \(\left\{ \begin{array}{l} x=1 \\ y=3 \end{array} \right. \) |
et donc \(S=\{(1,3)\}\).
On veut résoudre le système \( \left\{ \begin{array}{c} ax+by=c \\ a'x+b'y=c' \end{array} \right.\)
Ce système peut s'écrire sous la forme matricielle
\(AX=B\)
où \(A=\left( \begin{array}{cc} a&b\\ a'&b' \end{array} \right)\), \(X=\left( \begin{array}{c} x\\ y \end{array} \right)\) et \(B=\left( \begin{array}{c} c\\ c' \end{array} \right).\)
Si \(A\) est inversible alors
\(AX=B\Leftrightarrow X=A^{-1}B. \)
La solution du système est alors donnée par
\(X=\left( \begin{array}{c} x\\ y \end{array} \right) =A^{-1}B= \dfrac{1}{ab'-ba'}\left( \begin{array}{cc} b' & -b \\ -a' & a \end{array} \right) \cdot\left( \begin{array}{c} c\\ c' \end{array} \right) =\left( \begin{array}{c} \dfrac{b'c-bc'}{ab'-a'b}\\[4mm] \dfrac{ac'-a'c}{ab'-a'b} \end{array} \right)\)
Le système a donc une solution si le déterminant \(\det (A)=ab'-a'b\neq 0 \), c'est-à-dire si la matrice \(A\) est inversible.
Résolvons le même système que ci-dessus par cette méthode.
Le système
\(\left\{ \begin{array}{l} 3x+2y=9 \\ 4x=y+1 \end{array} \right.\)
peut s'écrire sous la forme matricielle
\(AX=B\)
où \(A=\left( \begin{array}{cc} 3&2\\ 4&-1 \end{array} \right)\) , \(X=\left( \begin{array}{c} x\\ y \end{array} \right)\) et \(B=\left( \begin{array}{c} 9\\ 1 \end{array} \right). \)
Puisque \(\det (A)=-3-8=-11\neq 0 \), la matrice \(A\) est inversible et la solution du système est donnée par
\(X=A^{-1}B \). On calcule
\(A^{-1}= \dfrac{1}{-11}\left( \begin{array}{cc} -1 & -2 \\ -4& 3 \end{array} \right) =\left( \begin{array}{cc} \dfrac{1}{11} & \dfrac{2}{11} \\ \dfrac{4}{11}& - \dfrac{3}{11} \end{array} \right)\)
et la solution du système est alors donnée par
\(X=\left( \begin{array}{c} x\\ y \end{array} \right) =A^{-1}B= \left( \begin{array}{cc} \dfrac{1}{11} & \dfrac{2}{11} \\ \dfrac{4}{11}& - \dfrac{3}{11} \end{array} \right) \cdot\left( \begin{array}{c} 9\\ 1 \end{array} \right) =\left( \begin{array}{c} \dfrac{11}{11}\\ \dfrac{33}{11} \end{array} \right) =\left( \begin{array}{c} 1\\ 3 \end{array} \right),\)
donc \(S=\{(1,3)\} \).
(c) Cas particuliers
- Système impossible
\( \left\{ \begin{array}{l} 3x-2y=5 \\ 6x-4y=2 \end{array} \right. \)
On a \(S=\emptyset\). En effet, les coefficients de \(x\) et \(y\) sont proportionnels mais pas les termes indépendants. Il s'agit de deux droites parallèles distinctes. - Système simplement indéterminé
\(\left\{ \begin{array}{l} 3x-2y=5 \\ 6x-4y=10 \end{array} \right.\)
On a \(S=\{(x,y)\in \mathbb R^{2}|3x-2y=5\}\). En effet, les deux équations ont des coefficients proportionnels. La deuxième équation est la multiplication de la première par un facteur \(2\). Il s'agit donc de la même droite. - Système doublement indéterminé
\(\left\{ \begin{array}{l} 6x-2y=2(3x-y) \\ -x-4y+4=4(1-y)-x \end{array} \right.\)
On a \(S= \mathbb R^{2}\). En effet, les deux équations de ce système sont équivalentes à l'équation \(0=0\) qui est toujours satisfaite quelles que soient les valeurs de \(x\) et de \(y\).
