Théorie du module : Géométrie et mesure

Périmètre et aire de surfaces élémentaires

Voici les formules permettant de calculer le périmètre et la surface de quelques formes géométriques de base.

(a) Disque et secteur

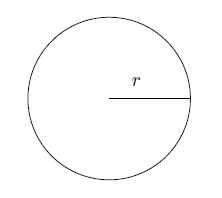
La longueur du cercle de rayon \(r\) a est le nombre \(l=2\pi r\). La surface du disque de rayon \(r\) est le nombre \(S=\pi\, r^2\).

La longueur de l'arc intercepté par un angle \(\alpha\) sur un cercle de rayon \(r\) est donnée par \(L=r\alpha\), où \(\alpha\) est mesuré en radians.

La surface du secteur circulaire de rayon \(r\) et d'angle \(\alpha\) est le nombre \(S=\dfrac{r^2\alpha}{2}\), où \(\alpha\) est mesuré en radians.

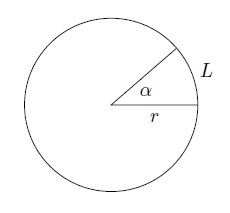
(b) Triangle

Le périmètre du triangle de côtés \(a\), \(b\), \(c\) est le nombre \(P=a+b+c\).
La surface du triangle de base \(B\) et de hauteur \(h\) est le nombre \(S=\dfrac{Bh}{2}\).

 

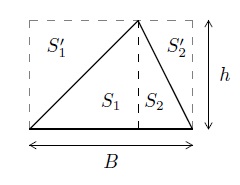
En effet, les surfaces \(S_1\) et \(S_1'\) ainsi que \(S_2\) et \(S_2'\) sont égales. La surface du triangle est donc la moitié de celle du rectangle dans lequel il est inscrit.

(c) Rectangle

Le rectangle de longueur \(L\) et de largeur \(l\) a pour périmètre le nombre \(P=2(L+l)\) et sa surface est le nombre \(S=Ll\).

 

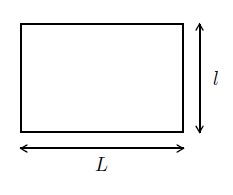
En particulier, le carré de côté \(c\) a pour périmètre le nombre \(P=4c\) et sa surface est le nombre \(S=c^2\).

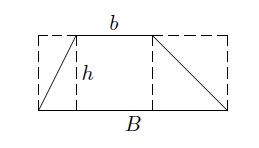
(d) Parallélogramme

Le périmètre d'un parallélogramme de côtés non parallèles \(B\) et \(b\) est le nombre \(P=2(B+b)\).
La surface du parallélogramme de base \(B\) et de hauteur \(h\) est le nombre \(S=Bh\).

 

En effet, si on découpe le triangle hachuré à gauche et qu'on le colle à droite, on retrouve l'aire du rectangle.

(e) Losange

Le losange de grande diagonale \(D\) et de petite diagonale \(d\) a pour périmètre le nombre \(P=2\sqrt{D^2+d^2}\) et sa surface est le nombre \(S=\dfrac{Dd}{2}\).

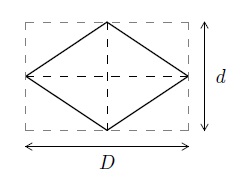
En effet, la surface du losange est la moitié de celle du rectangle dans lequel il est inscrit.
Son périmètre vaut \(4c\) où \(c\) est la longueur du côté. Comme les diagonales sont perpendiculaires entre elles et se coupent en leur milieu, on déduit du Théorème de Pythagore que

\(c^2=\left(\dfrac{D}{2}\right)^2+\left(\dfrac{d}{2}\right)^2\mbox{ d'où }c=\sqrt{\frac{D^2}{4}+\frac{d^2}{4}}=\frac{1}{2}\sqrt{D^2+d^2}.\)

Le périmètre vaut donc \(P=4c=2\sqrt{D^2+d^2}\).

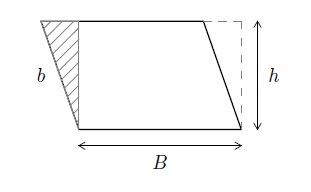
(f) Trapèze

Le trapèze de grande base \(B\), de petite base \(b\) et de hauteur \(h\) a pour surface le nombre
\(S=\frac{1}{2}(B+b)h\).

En effet, l'aire du trapèze est donnée par \(bh+\dfrac{1}{2}(B-b)h=\dfrac{1}{2}(B+b)h\).