Théorie du module : Géométrie et mesure
Table des matières
- Théorème de Thalès et proportions
- Cercles
- Polygones
- Triangles
- Quadrilatères
- Périmètre et aire de surfaces élémentaires
- Volume de solides élémentaires
- Mesures et grandeurs
- Exemples détaillés
Polygones
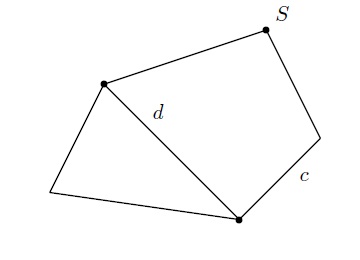
Un polygone est une figure plane délimitée par une ligne fermée constituée de segments de droite. Ces segments sont les côtés (\(c\)) du polygone et le point d'intersection de deux côtés est appelé sommet (\(S\)) du polygone. Une diagonale (\(d\)) d'un polygone est un segment de droite qui joint deux sommets non consécutifs. Un polygone est convexe si tout segment ayant ses extrémités sur le polygone y est inclus tout entier. Dans la suite, on ne considérera que des polygones convexes.
Un polygone est régulier si tous ses côtés ont même longueur et tous ses angles intérieurs ont même amplitude. Voici un tableau reprenant les principaux polygones réguliers, avec leur nombre de côtés et l'amplitude de leurs angles intérieurs :
| polygone | Nombre de côtés | Amplitude des angles |
| triange | 3 | \(60^{\circ}\) |
| carré | 4 | \(90^{\circ}\) |
| pentagone | 5 | \(108^{\circ}\) |
| hexagone | 6 | \(120^{\circ}\) |
| heptagone | 7 | \(128,57^{\circ}\) |
| octogone | 8 | \(135^{\circ}\) |
| décagone | 10 | \(144^{\circ}\) |
| dodécagone | 12 | \(150^{\circ}\) |
Les polygones réguliers possèdent les propriétés suivantes :
- Tout polygone régulier admet un axe de symétrie.
- Tout polygone régulier peut être inscrit dans un cercle.
En effet, si le polygone a un nombre impair de côtés, toute droite joignant un sommet au milieu du côté opposé est un axe de symétrie. Si le polygone a un nombre pair de côtés, toute droite joignant un sommet au sommet opposé est un axe de symétrie et toute droite joignant le milieu de deux côtés opposés est aussi un axe de symétrie.
Tous les axes de symétrie d'un polygone se coupent en un point qui est le centre d'un cercle dans lequel on peut inscrire le polygone. Le cercle circonscrit au polygone est le cercle centré en ce point et passant par tous les sommets du polygone.
