Théorie du module : Repères et vecteurs
Table des matières
- Le plan \(\mathbb{R}^2\)
- L'espace \(\mathbb{R}^3\)
- La notion de vecteur
- Opérations sur les vecteurs
- Vecteurs et points particuliers
- Exemples détaillés
La notion de vecteur
Nous présentons cette notion dans le plan (\(\mathbb{R}^2\)) et dans l'espace \((\mathbb{R}^3)\). Des quantités comme l'aire, le volume, la longueur, la température et le temps n'ont qu'une intensité et peuvent être entièrement représentées par un nombre réel (accompagné de l'unité de mesure adéquate). Une grandeur de ce type est une grandeur scalaire et le nombre correspondant est un scalaire. Des concepts tels que la vitesse ou la force ont à la fois une intensité, un sens et une direction. En physique, on appelle vecteur une quantité caractérisée par une longueur (ou intensité ou grandeur), par une direction et par un sens dans cette direction. Citons comme illustrations, l'effet d'un champ magnétique dans l'espace avec son intensité et sa direction; l'effet d'une force appliquée en un point caractérisée par une intensité et une direction; un avion qui se déplace avec une certaine vitesse dans une certaine direction ; un déplacement dans le plan caractérisé par une longueur ou distance et une direction.
Supposons que l'on déplace un objet d'une position \(A\) à une position \(B\). On peut représenter ce déplacement par un segment fléché, la pointe de la flèche étant placée au point \(B\) et l'origine en \(A\), pour indiquer que le mouvement s'est effectué de \(A\) vers \(B\). On utilise alors \(\overrightarrow{AB}\) comme notation pour le vecteur. Il est important de réaliser qu'un vecteur est entièrement caractérisé par sa longueur et sa direction. L'endroit où l'on place dans le plan, ou dans l'espace, l'origine d'un vecteur est sans importance, seules comptent sa longueur et sa direction.
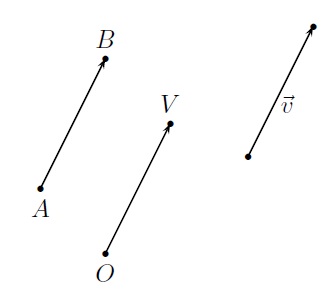
Dans la figure ci-dessus, \(\overrightarrow{AB}\) et \(\overrightarrow{OV}\) définissent le même vecteur que l'on pourrait représenter par le symbole \(\vec{v}\). En d'autres termes, un vecteur est défini indépendamment de la position où on le place dans le plan ou dans l'espace. Mathématiquement, tous les segments fléchés de même longueur et de même direction sont équivalents (on dit qu'ils forment une classe d'équivalence) et peuvent être représentés par n'importe lequel d'entre eux.
(a) Vecteurs du plan \(\mathbb{R}^2\)
Considérons un repère cartésien orthonormé. En plaçant l'origine du vecteur \(\vec{v}\) à l'origine du repère, on obtient le point \(V\) qui est l'extrémité de \(\vec{v}\). On a donc \(\vec{v}=\overrightarrow{OV}\). Le point \(V\) est un point du plan et a donc des coordonnées : \(V=(v_x,v_y)\). Les composantes du vecteur \(\vec{v}\) sont les coordonnées du point \(V\). On écrira \(\vec{v}=(v_x,v_y)\).
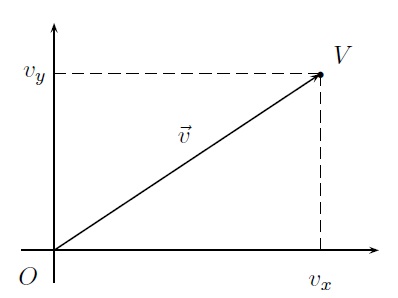
Si \((x_a,y_a)\) et \((x_b,y_b)\) sont respectivement les coordonnées des points \(A\) et \(B\), le vecteur \(\overrightarrow{AB}\) ou \(\vec{u}\) qu'ils définissent, a pour composantes \((u_x,u_y)=(x_b-x_a,y_b-y_a)\). En effet, le vecteur \(\overrightarrow{AB}\) peut être identifié au vecteur \(\overrightarrow{OU}\).
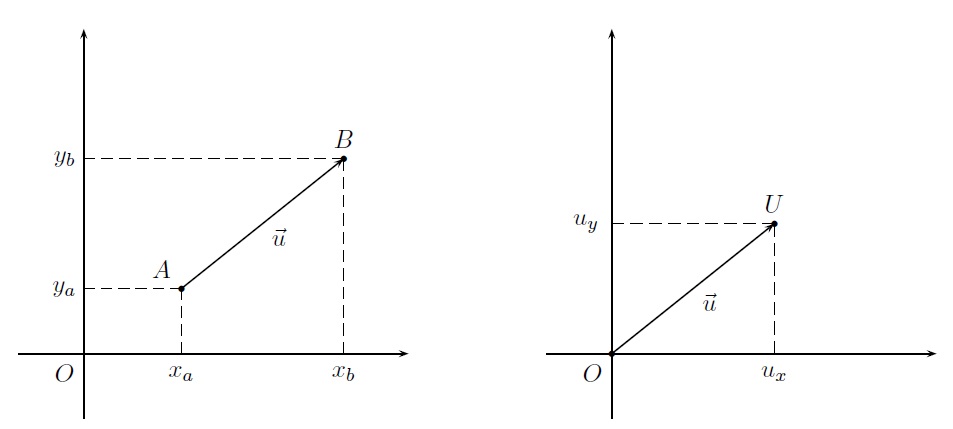
\(\|\vec{v}\| =\sqrt{v_x^2+v_y^2}.\)
Si \(\vec{u}=\overrightarrow{AB}=(x_b-x_a,y_b-y_a)\) alors\(\|\vec{u}\| =\|\overrightarrow{AB}\| =\sqrt{(x_b-x_a)^2+(y_b-y_a)^2}.\)
Il ne s'agit de rien d'autre que de l'application du Théorème de Pythagore.
Dans le plan, si un vecteur \(\vec{v}\) est connu par sa longueur \(\|\vec{v}\|\) et par l'angle \(\theta\) (mesuré dans le sens contraire des aiguilles d'une montre) qu'il forme avec l'axe horizontal, on en détermine aisément les composantes \((v_x,v_y)\) par
\(v_x=\|\vec{v}\|\cos\theta,\quad v_y=\|\vec{v}\|\sin\theta.\)
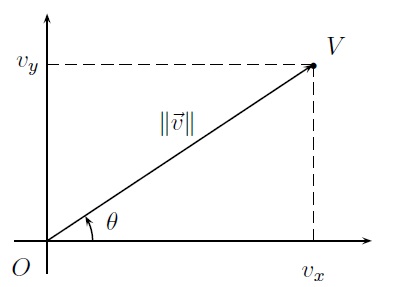
Inversément, on détermine la longueur \(\|\vec{v}\|\) d'un vecteur \(\vec{v}\), ainsi que l'angle \(\theta\) qu'il forme avec l'axe horizontal par
\(\|\vec{v}\|=\sqrt{v_x^2+v_y^2}, \quad \tan\theta=v_y/v_x,\)
pour \(v_x\neq 0\), ce qui nous permet de trouver \(\theta\), en y ajoutant au besoin \(\pi\) selon les signes de \(v_x\) et \(v_y\).
Pour plus de détails, vous pouvez consulter le chapitre de trigonométrie.
Par exemple, si le vent souffle à 12km/h dans la direction N\(40^\circ\)W, on peut exprimer sa vitesse par un vecteur \(\vec{v}\). La direction N\(40^\circ\)W correspond à un angle de \(130^\circ\). On a donc
\( \vec{v}= (v_x,v_y)= (\|\vec{v}\| \cos 130^\circ,\|\vec{v}\| \sin 130^\circ) = (-7,7; 9,2).\)
(b) Vecteurs de l'espace \(\mathbb{R}^3\)
Dans le cas de vecteurs dans l'espace, on parlera de triplets ordonnés de nombres réels. Par exemple, le vecteur \(\vec{v}=\overrightarrow{OV}=(v_x,v_y,v_z)\).
Si \((x_a,y_a,z_a)\) et \((x_b,y_b,z_b)\) sont respectivement les coordonnées des points \(A\) et \(B\), le vecteur \(\overrightarrow{AB}\) ou \(\vec{u}\) qu'ils définissent, a pour composantes \((u_x,u_y)=(x_b-x_a,y_b-y_a,z_b-z_a)\).
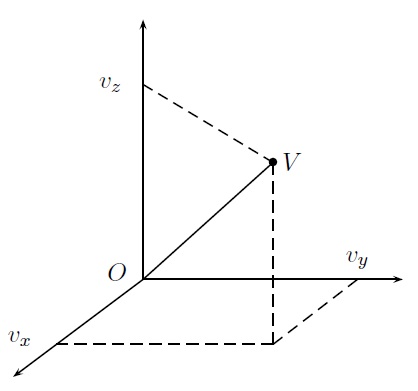
La définition de norme s'étend sans difficulté aux cas du vecteur dans l'espace.
\(\|\vec{v}\| =\sqrt{v_x^2+v_y^2+v_z^2}.\)
Si \(\vec{u}=\overrightarrow{AB}=(b_x-a_x,b_y-a_y,b_z-a_z)\) alors\(\|\vec{u}\| =\|\overrightarrow{AB}\| =\sqrt{(b_x-a_x)^2+(b_y-a_y)^2+(b_z-a_z)^2}.\)
Par exemple, considérons le vecteur \(\vec{u}=\overrightarrow{AB}\) où \(A=(3,1,-2)\) et \(B=(-2,7,-4)\).
Les composantes du vecteur \(\vec{u}\) se calculent par la différence entre les coordonnées du point \(B\) et celles du point \(A\) :
\(\vec{u}=(-2-3,7-1,-4+2)=(-5,6,-2).\)
La norme du vecteur \(\vec{u}\) se calcule par la formule
\(\|\vec{u}\|=\sqrt{(-5)^2+6^2+(-2)^2}=\sqrt{65}.\)
